The Korean Society For New And Renewable Energy

[ Article ]

New & Renewable Energy - Vol. 12, No. s2, pp.30-35

ISSN: 1738-3935 (Print)

Article No. [2016-10-PV-004]

Print publication date Oct 2016

Received 31 May 2016 Revised 29 Jun 2016 Accepted 12 Jul 2016

DOI: https://doi.org/10.7849/ksnre.2016.10.12.s2.30

국내의 시간에 따른 수평면전일사량 상관식 제안 및 정확성 평가(I)

김하양¹⁾ ; 김정배¹⁾^{, *}

Correlation to Predict Global Solar Insolation and Evaluation of that Correlation for Korea(I)

Ha-Yang Kim¹⁾ ; Jeongbae Kim¹⁾^{, *}

1)Dept. of Energy System Engineering, Korea National University of Transportation

Correspondence to: Dept. of Energy System Engineering, Korea National University of Transportation E-mail: jeongbae_kim@ut.ac.kr Tel: +82-43-841-5282 Fax: +82-43-841-5280

Copyright © 2016 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Recently, several studies have been conducted to show how the horizontal global solar radiation in Korea can be predicted using the Zhang-Huang (ZH) model proposed in 2002 for China. Previous results showed that that Cloud-cover Radiation Model (CRM) is unsuitable for Korea. Therefore, this study first corrected the coefficients of the ZH model to make it applicable to Korea and showed that ZH fitted model could make a prediction. This work added a term with the duration of sunshine as being closely related to the hourly solar radiation in Korea into the ZH model. Finally, this study proposed a new model to predict the hourly and daily total solar radiation for all regions, various seasons, and various weather conditions, including overcast and clear, with higher accuracy and lower error than other models proposed in Korea.

Keywords:

Hourly horizontal global radiation, ZHM, Estimation of solar radiation, Dry-bulb temperature, Relative humidity, Cloud cover, Duration of sunshine, Wind velocity

키워드:

시간 수평면전일사량, Zhang and Huang model, Z&H 모델, 일사량 예측, 건구온도, 상대습도, 운량, 일조시간, 풍속

1. 서 론

우리나라의 신재생에너지 자원의 부존량의 평가와 평가 결과를 활용하는 예측 상관식을 제시하는 것은 매우 중요하다. 특히, 신재생에너지의 대표 분야 중의 하나인 태양광 분야는 태양에너지 자원량의 정확한 예측이 매우 필요하고 또한 중요하다.^[1,2,3]

특히, 수평면전일사량의 측정지역은 전국적으로 15개 지역(춘천, 강릉, 서울, 원주, 서산, 청주, 대전, 포항, 대구, 전주, 광주, 진주, 부산, 목포, 제주)뿐이지만, 건구온도 등을 포함하는 기상 관측데이터의 측정개소는 300개 이상이므로, 태양에너지 분야의 보급사업의 수행지역이 확대됨에 따라 태양광 및 태양열 시스템의 설계를 위한 기초 자료로서 해당지역에 대한 정확한 일사량 예측자료가 필요하다.^[1]

1982~2008년까지의 전국 16개 지역에서의 측정된 수평면전일사량을 기준으로 온도, 습도, 일조시간과 운량 중에서 운량을 선택하여 월평균 1일 대기권 밖 일사량과 수평면전일사량과의 비를 지역별로 제시하였다.^[4]

1982~2010년까지의 전국 16개 지역에서의 수평면 전일사량 측정값을 이론적으로 예측하는 식과 비교하고, 이를 보정하기 위하여 16개 지역에서 측정하고 있는 건구 온도, 상대 습도, 일조시간과 운량 중에서 운량과 일조시간을 선택하여 월평균 1일 대기권 밖 일사량과 수평면전일사량과의 비를 지역별로 제시하였다. 다만, 지역별 일조율 상수의 오차가 약 15.8% 정도 수준에 머물러 있음을 알 수 있다. 또한, 논문의 결론에서 제시하는 것과 같이 현재 기상청에서 측정하고 있는 일조, 운량, 건구 온도, 상대 습도 전체를 고려하는 일사량과의 관계 규명 이후에 기상 관측 변수를 포함하는 일사량 예측식의 필요성을 강조하였다.^[5] 이와 함께 Cloud-cover 복사 모델^[6](CRM, Cloud-cover Radiation Model)은 한국에 적용하기 어려움도 제시하였다.

최근에, 시간에 따른 정확한 일사량의 예측을 위한 다양한 기존의 연구결과들을 평가하여 건구온도, 상대습도, 일조시간 및 운량의 기상 관측 변수를 포함하는 예측식이 필요하고, 수평면전일사량을 예측하기 위하여 전국 혹은 위도별로 적용 가능한 한국형 모델식이 필요함을 제안하였다.^[1]

기상 측정 데이터를 이용하여 중국의 시간별 수평면전일사량을 예측하기 위해 Zhang&Hwang은 운량, 건구온도, 상대습도, 및 풍속을 포함하는 식 (1)을 제안하였고 중국 전역(북경에서 광주까지)에 대해 일정한 계수로서 높은 정확도를 얻을 수 있음을 보여주었다.^[7]

I = I 0 sin h β 0 + β 1 CC + β 2 CC 2 + β 3 T db, n - T db, n - 3 + β 4 RH + β 5 V w + d / k

(1)

여기서, I는 수평면전일사량(W/m²), I₀는 태양 상수(1355 W/m²), h는 고도각, CC는 0~1로 측정된 운량, T_db,n은 n시간의 건구온도, RH는 상대습도(%), V_w는 풍속(m/s), d와 k 그리고 β₀∼β₅는 상수 계수들이며 아래와 같다.

d=-17.853, k=0.843,
β₀=0.5598, β₁=0.4982, β₂=-0.6762,
β₃=0.02842, β₄=-0.00317, β₅=0.014

최근에 Zhang&Hwang 모델(이하, Z&H 모델)을 기본으로 하여 미국의 텍사스주에 대하여 새로운 계수를 찾고, 새롭게 얻어진 계수를 이용하여 텍사스주의 대부분의 지역에 대하여 수평면전일사량의 예측이 정확할 수 있음을 확인하였다.^[8]

따라서, 본 연구에서도 Z&H 모델을 기본으로 하여 중국의 계수를 그대로 적용하는 경우와 한국에 대하여 새롭게 계수를 찾은 경우의 결과를 비교하면서 Z&H 모델에 바탕을 둔 수평면전일사량 예측식의 적용 가능성을 평가하였다.

또한, 15개 지역의 기상 측정 변수들과 수평면전일사량의 관계를 분석하여 Z&H 모델에 반드시 필요한 새로운 기상 변수를 추가하여 한국형 예측 모델을 제시하고자 하였다.

2. 해석적 방법과 예측식 결과

한국에 대하여 식 (1)의 새로운 계수를 찾기 위하여, 최근 5년 이내에 일사량을 측정하고 있는 15개 지역에 대하여 일사량과 기상 데이터가 제대로 갖추어져 있는 2012년을 선정하였다.

식의 계수를 구하기 위하여 15개 지역에 대해 365일이 아닌 봄, 여름, 겨울의 청명일 3일(1월 14일, 5월 6일, 8월 5일)과 비청명일 3일(1월 3일, 5월 13일, 8월 2일)의 90개 데이터 세트로 Minitab(미니탭)을 이용하였다.

다만, 2012년의 15개 지역에 대한 기상데이터들을 면밀히 검토한 결과, 가을의 기상 데이터들이 봄과 거의 동일한 특성을 가지고 있어 가을을 제외하고 고려한 것이다.

청명일은 15개 지역 전체가 청명도가 높은 날을, 비청명일은 전체 지역에 대하여 청명도가 낮은 날로 선정하였다(365일/15개 지역 모두를 고려한 계수와 거의 차이가 없음).

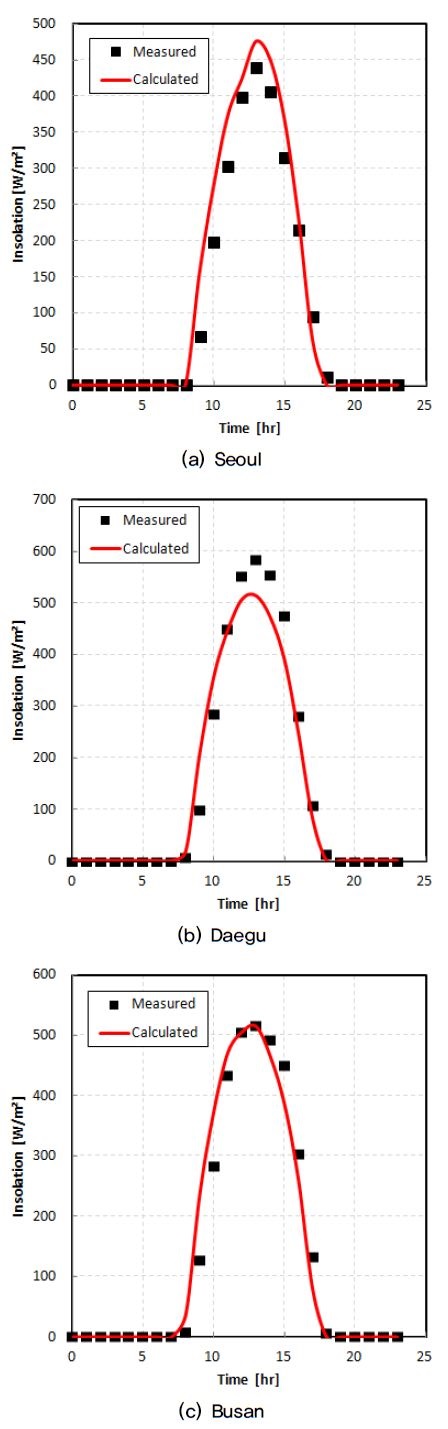
식 (1)의 계수 변경없이 시간에 따라 계산된 수평면전일사량은 Fig. 1(a)와 같이 특정 청명일의 특정 지역에 대해서는 측정 일사량과 비교하여 잘 예측하는 것처럼 나타나기도 하지만, Fig. 1(b)에서와 같이 상당히 큰 오차를 가진 것으로 나타나고 있다.

Fig. 1.

Solar radiation with time using Z&H model

그리고, 서론에서 설명한 것과 같이 시간에 따라 측정된 15개 지역의 6일 데이터를 활용하여 Z&H 모델의 계수들을 미니탭을 이용하여 구하고, 계수만 달라진 식을 Z&H 피팅 모델(Z&H fitted model)이라 지정하였다.

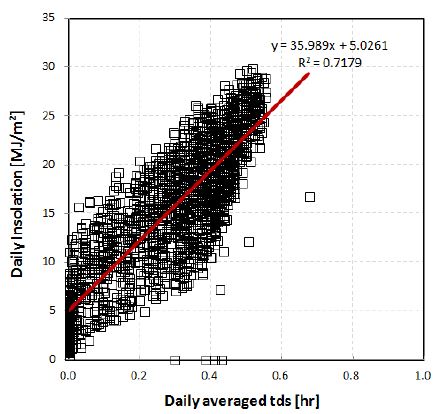
현재 기상청에서 측정하고 있는 기상 데이터(건구 온도, 상대습도, 운량, 일조시간, 풍속) 중에서 수평면전일사량과의 상관성이 가장 높은 것으로 나타나는(Fig. 2 참조) 일조시간(t_ds)을 포함하여 식 (2)로 Z&H 모델을 수정하였다.

Fig. 2.

Daily total solar radiation and daily averaged tds for 15 regions during 2012

이러한 과정 속에서 식의 상수 계수들인 d와 k는 물리적인 의미를 가진 부분이 아니므로, 식의 단순화를 위하여 d=0으로 k=1로 선정하여 한국형 모델식(KKP 모델)을 제시하였다.

I = I 0 sin h β 0 + β 1 CC + β 2 CC 2 + β 3 T db, n - T db, n - 3 + β 4 RH + β 5 V w + β 6 t ds

(2)

3. 예측식의 특성과 정확성

세가지 일사량 예측식에 대한 각각의 계수들의 값을 Table 1에 나타내었다. Z&H 모델의 한국형 계수는 중국의 계수와 상당히 차이가 남을 알 수 있다. Z&H 피팅 모델의 일사량 예측 정확도는 아래에서 설명할 것이다.

Table 1.

Coefficients for three models to calculate solar radiation

앞서 Fig. 1에 식 (1)의 Z&H 모델식을 그대로 적용할 때의 예측식의 특성을 설명하였다.

이와 아울러 KKP 예측 모델의 시간에 따른 수평면전일사량의 예측 특성은 먼저 비청명일이었던 2012년 1월 3일에 대한 Fig. 3과 같이, 청명일이었던 2012년 1월 4일에 대한 Fig. 4와 같이 청명일과 비청명에 관계없이 그리고 지역의 위치에 관계없이 정확도가 매우 높게 계산값이 측정값을 잘 예측하고 있음을 알 수 있다. 다만, 그래프에서 육안으로 보이는 것과 실제로 특정 시간에 수직으로의 계산값과 측정값의 차이는 다소 다를 수 있다.

Fig. 3.

Solar radiation in overcast Jan. 3 2012 with time using KKP model

Fig. 4.

Solar radiation in clear Jan. 14 2012 with time using KKP model

Z&H 모델, Z&H 피팅 모델 및 KKP 한국형 모델에 대한 수평면전일사량의 예측 정확도와 오차 특성을 평가하기 위하여 먼저 식 (3)과 같이 R², 식 (4)와 같이 MBE(Mean bias error), 식 (5)와 같이 RMSE(Root mean square error), 식 (6)과 같이 1일 총일사량 정확도(A_total), 그리고 식 (7)과 같이 일사량 피크 정확도(A_peak)를 고려하였다. 특히, 다른 일사량 예측 모델 연구에서 고려하지 않았던 시간에 따른 계산 일사량의 정확도를 1일 총일사량과 피크 시간에서의 정확도로 구분하여 평가하였다.

R 2 = Σ I cal - I avg Σ I meas - I avg

(3)

MBE = Σ I cal - I meas n

(4)

R MBE = Σ I cal - I meas 2 n

(5)

A_total = 1 - Σ I cal - Σ I meas Σ I meas × 100

(6)

A_peak = 1 - I cal, peak - I meas, peak I meas, peak × 100

(7)

여기서, I_cal는 계산 수평면전일사량(W/m²), I_meas는 측정 수평면전일사량(W/m²), I_avg는 1일 평균 수평면전일사량(W/m²)을 나타낸다.

식 (3)에서 식 (7)까지의 정확도와 오차 평가식에 대하여 세가지 모델에 대하여 평가한 결과를 Table 2에 나타내었다. 표에서와 같이 전체 항목에 대하여 KKP 모델이 정확도가 높고 오차가 가장 적게 나타나고 있음을 알 수 있다. Z&H 모델은 기본으로 하여 계수만 국내 기상 데이터로 얻은 Z&H 피팅 모델의 정확도가 KKP 모델에 비교될 만큼 높은 것으로 나타나므로 Z&H 모델을 기준 예측 모델로 정한 것은 합리적인 것으로 판단된다.

Table 2.

Prediction accuracies and errors for three models to calculate solar radiation

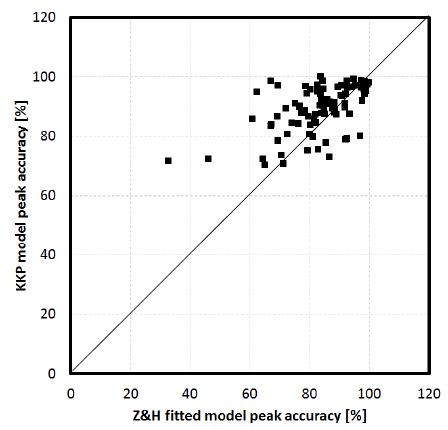
특히, 1일 총 일사량의 정확도는 높더라도 일사량 피크 시간에서의 계산값의 정확도는 실제로는 낮은게 보통이다. Z&H fitted와 비교했을 때 R²와 A_peak는 약 6% 정도, MBE와 RMSE는 비슷한 수준을 보이는데, 실제로는 Fig. 5에서와 같이 피크 일치율이 상대적으로 KKP 모델의 평균 6% 정도 높은 것이 매우 중요하고 피크 시간도 정확하게 예측하고 있어 KKP 모델의 예측 정확도가 우수한 것으로 판단된다.

Fig. 5.

Peak calculation accuracy between Z&H fitted and KKP models

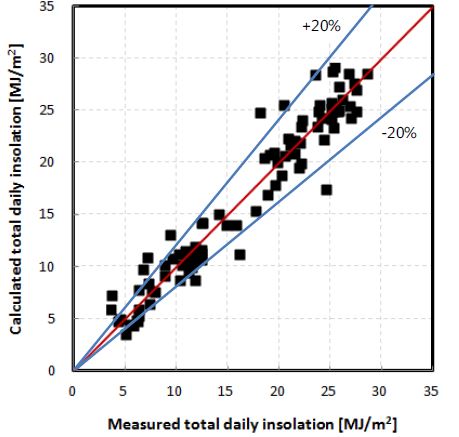
마지막으로 KKP 모델로 계산된 시간에 따른 수평면전일사량으로부터 얻어진 1일 총 수평면전일사량을 측정된 수평면전일사량과 비교하여 Fig. 5에 나타내었다.

Fig. 6에서와 같이 90의 데이터 중에서 측정 1일 총 수평면전일사량에서 ±20%를 벗어나는 경우는 8개 정도이며 거의 대부분 일사량이 낮았던 날과 지역에 대한 것으로 나타났다. 따라서, KKP 모델 예측식은 전국적으로 청명도가 아주 낮은 경우에는 50% 정도의 1일 총 수평면전일사량의 오차를 가지지만, 그러한 경우를 제외한 지역과 일기 조건에서는 시간에 따른 일사량 예측에 적용 가능성이 매우 높음을 알 수 있었다.

Fig. 6.

Solar radiation for 90 samples using KKP model

그럼에도, 추후 2012년 15개 지역과 전체 365일에 대하여 KKP 모델로 평가한 결과의 제시, 국내의 기상 데이터 관측소들의 측정 데이터 상황을 포함하여 다양한 관측소의 여건을 고려하여 KKP 모델의 수정, 그리고 수평면총일사량을 직달과 산란으로 구분하여 계산할 수 있는 모델의 추가가 필요하다.

4. 결 론

이상과 같은 연구결과로부터 아래와 같은 결론을 도출하였다.

1) Z&H 모델식을 활용하여 이를 국내에 적합한 수평면전일사량 예측식으로 수정하는 것이 매우 바람직함을 알 수 있었다.
2)국내의 측정 기상 데이터 중에서 가장 수평면전일사량과 상관성이 높은 일조시간을 Z&H 모델에 추가하면 예측 정확도를 높일 수 있음을 확인하였다.
3)특히, KKP 모델은 1일 총 수평면전일사량의 예측 정확도는 평균적으로 약 88.2% 수준이었으며, 1일 피크 시간에서의 피크 오차율도 약 89.0%를 나타내어 전국적으로 청명도가 아주 낮은 경우에는 50% 정도의 1일 총 수평면전일사량의 오차를 가지지만, 그러한 경우를 제외한 지역과 일기 조건에서는 관계없이 적용 가능성이 매우 높음을 알 수 있었다.
4)KKP 모델은 고도각, 운량, 건구온도, 상대습도, 풍속 및 일조시간을 고려하는 모델로 아래와 같다.

I = I 0 sin h β 0 + β 1 CC + β 2 CC 2 + β 3 T db, n - T db, n - 3 + β 4 RH + β 5 V w + β 6 t ds

β₀=0.4545, β₁=0.0577, β₂=0.0906,
β₃=-0.01408, β₄=-0.3193, β₅=0.00452,
β₆=0.371

References

Kim, H. Y., and Kim , J., (2016), “Prediction Correlation of Solar Insolation using Relationships between Meteorological Data and Solar Insolation in 2012(I)”, Journal of KSES, 36(1), p1-9. [https://doi.org/10.7836/kses.2016.36.1.001]
Lee, K. T., Zo, I. S., Jee, J. B., and Choi, Y. J., (2011), “Temporal and Spatial Distributions of the Surface Solar Radiation by Spatial Resolutions on Korea Peninsula”, New & Renewable Energy, 7(1), p22-28. [https://doi.org/10.7849/ksnre.2011.7.1.022]
Jee, J. B., Lee, S. W., Choi, Y. J., and Lee, K. T., (2012), “The Generation of Typical Meteorological Year for Research of the Solar Energy on the Korean Peninsula”, New & Renewable Energy, 8(2), p12-23. [https://doi.org/10.7849/ksnre.2012.8.2.014]
Jo, D. K., and Kang, Y. H., (2010), “A Study on the Solar Radiation Estimation of 16 Areas in Korea Using Cloud Cover”, Journal of KSES, 30(4), p15-21.
Jo, D. K., Yun, C. Y., Kim, K. D., and Kang, Y. H., (2012), “A Study on the Estimating Solar Radiation in Korea Using Cloud Cover and Hours of Bright Sunshine”, Journal of KSES, 32(2), p28-34. [https://doi.org/10.7836/kses.2012.32.2.028]
Munner, T., and Gul, M. S., (2000), “Evaluation of Sunshine and Cloud Cover based Models for Generating Solar Radiation Data”, Energy Conversion and Management, 41, p461-482. [https://doi.org/10.1016/S0196-8904(99)00108-9]
Zhang, Q. Y., and Huang, Y. J., (2002), “Development of Typical Year Weather Files for Chinese locations”, ASHRAE Transactions, 108(2), p1063-1075.
Kim, K. H., Baltazar, J. C., and Haberl, J. S., (2014), “Evaluation of Meteorological Base Models for Estimating Hourly Global Solar Radiation in Texas”, Energy Procedia, 57, p1189-1198. [https://doi.org/10.1016/j.egypro.2014.10.106]