천리안 기상위성을 이용한 한반도 지역의 Linke turbidity 및 청천일사량 추정

1. 서 론

지표면에 도달하는 태양 복사의 세기를 일사량이라고 하며, 일사량을 측정하는 것은 기상 분석을 위한 기초연구 뿐 만 아니라 태양광을 활용하는 신재생에너지 사업에도 매우 중요하다. 일사량은 지상 관측소에서 취득 가능하나, 위치 및 설치비용의 한계로 인하여 모든 지역의 일사량 정보를 취득하기 어렵다. 반면, 위성영상의 경우 광범위한 범위와 시간변화에 따른 태양에너지를 효율적으로 분석할 수 있고, 관측소 설치가 불가능한 비접근 지역에 대한 일사량 정보를 취득할 수 있다는 점에서 기상위성을 활용한 일사량 추정에 대한 연구가 꾸준히 진행되고 있다.^[1~3] 특히 유럽의 경우에는 자국의 기상위성과 물리모델을 활용하여 일사량을 추정하는 연구가 체계적으로 진행되고 있으며 다양한 연구를 통하여 위성영상 기반으로 추정된 일사량의 정확도가 검증되고 있다.^[4]

구름이 없는 맑은 하늘의 일사량(청천일사량)을 추정하는 것은 위성영상 기반의 일사량 추정 기법에서 매우 중요한 단계이다.^[2] 청천일사량은 청천일 모델(clear sky model)을 통하여 계산되는데, 입력변수와 계산 방법에 따라 다양한 모델이 존재한다.^[5] 청천일 모델의 가장 중요한 인자는 대기의 상태를 나타낼 수 있는 대기 중 에어로졸(aerosol) 및 수증기(water vapour) 등이 있는데, 이러한 정보는 원하는 지역의 값을 실시간으로 얻기 힘들다는 문제가 존재한다. 따라서 일반적으로 영상기반의 일사량 추정 모델에서는 대기의 상태를 반영하는 대기혼탁인자를 사용하고 있으며, 대표적으로 Linke turbidity factor가 쓰인다(이하 TL).^[2] 이는 맑고 건조한 하늘에서의 직달 일사량이 소산되는 정도를 나타내며 대기 중 에어로졸, 수증기 및 오존의 양과 관련된 값으로 1(맑은 하늘)~7(오염된 하늘)사이의 값을 나타내며,^[6] Linke turbidity의 정확도는 청천일사량 추정치의 정확도를 향상시킨다는 연구결과도 존재한다.^[7]

SoDa에서는 NASA의 가강수량 정보와 AERONET에서 제공하는 에어로졸 정보 등을 고려하여 지구 전 지역에 대한 월별 평균 TL 값을 제공한다.^[8] 해당 자료는 위도와 경도를 기준으로 각각 0.083°간격으로 구분(약 10km)되며, 실측치와의 RMSE는 0.7(TL units)로 알려져 있다(Fig. 1).^[9]

Fig. 1.

Example of a monthly map of the Linke turbidity for the world. These maps can be downloaded from the Solar Radiation Data website.[8]

유럽의 Heliosat 모델을 비롯한 기존의 다양한 선행연구에서 SoDa에서 제공하는 TL 값을 사용하였으나,^[5,10] 낮은 시간과 공간 해상도로 인하여 연구지역에 최적화된 TL값을 직접 계산하는 연구가 수행되고 있다.^[11~12] 그러나 대부분 직달일사량(beam irradiance) 및 전일사량(global irradiance)을 사용하여 TL값을 계산하였으며,^[6,11] 다양한 지역에서 취득된 시간별 지상 실측치 자료를 활용하였다.^[6,12~13]

국내의 경우, 산발적으로 퍼져있는 지상관측소로 광범위한 지역의 지상 자료를 취득하기 어려운 상황이며, 위성영상으로부터 일사량을 구하기 위하여 TL값이 필요한 상황을 고려하여, 본 연구에서는 국내에서 운용되는 통신해양기상위성인 천리안(COMS: Communication, Ocean and Meteorological Satellite)에서 취득된 에어로졸광학두께(AOD; Aerosol Optical Depth) 및 가강수량(TPW; Total Precipitable Water) 정보를 활용하여 국내에 최적화된 TL을 계산하고자 하였다. 또한 최종적으로 청천일 모델을 적용하여 계산된 청천일사량의 정확도를 분석하고 그 활용가능성을 평가하였다. 이를 위하여 실제 지상 관측소에서 취득된 일사량을 참조자료로 하여 계산된 TL과 SoDa에서 구축된 자료를 사용한 청천일사량의 시기와 위치에 따른 rRMSE(relative Root Mean Square)와 rMBE(relative Mean Bias Error)값을 분석하였다.

2. 실험 자료 및 방법

2.1 실험 자료

2.1.1 천리안 기상 위성 자료

본 연구에서는 국내에서 운용되는 천리안 기상위성의 영상자료를 활용하여 한반도 지역의 TL을 계산하며, 이 값을 이용하여 최종적으로 청천일사량을 구하고자 한다. 이를 위해서 천리안 기상위성에서 제공하는 가시영상(visible image)및 AOD와 TPW자료를 사용하였다.

1) 가시영상

천리안 위성은 1km의 공간해상도를 갖는 가시영상과, 공간해상도 4km의 적외선 및 단파적외영상 등 총 5개의 파장영역에서 영상을 제공한다. 가시영상은 0.4~0.7㎛ 파장에서 영상을 취득하며 하층운, 안개 등 기상현상을 식별하는데 유용하게 활용된다. 본 연구에서는 2013년 1월~11월 사이의 한반도 지역을 촬영한 가시영상을 취득하였으며, 이는 청천일일사량 및 구름의 판단 유무를 분석하기 위하여 사용되었다.

2) AOD

AOD는 위성으로부터 취득된 영상에서 에어로졸의 양을 표현할 수 있는 변수로써, 대기에 존재하는 에어로졸이 지면에서 대기상한까지 진행하는 복사에너지를 산란 또는 흡수하여 소산시키는 정도를 계수로 표현하여 적분한 값을 나타낸다. 천리안 위성자료 처리시스템(CMDPS: COMS Meteorological Data Processing System)에서는 AOD 외 15종의 기상산출물을 4km의 해상도로 제공하는데,^[14] 본 연구에서는 가시영상과 동일한 해상도를 얻기 위하여 최근린보간법(nearest neighbor interpolation)을 사용하였으며, 보정된 AOD 영상을 이용하여 Angstrom 지수 중 β변수를 산출하였다. Angstrom 변수는 에어로졸의 크기와 분포의 특징을 설명하는 인자로 TL을 계산하는데 사용된다.^[13]

3) TPW

TPW는 대류권내의 수증기가 응결되었을 때, 각 화소별 수증기량을 mm단위로 예측한 것을 의미한다. 수증기의 양은 시간과 공간에 따라 유동적으로 변하기 때문에 대기 중 수분의 양과 분포를 파악하기 위하여 사용되는 변수이다.^[14] AOD와 마찬가지로 가시영상과 동일기간의 자료를 수집하였으며, 최근린보간법을 사용하여 가시영상과 해상도를 일치시켰다. TPW는 TL을 계산하기 위하여 필요하며 본 연구에서 산출된 TL은 TPW의 이차함수 형태로 나타난다(식 (1)).^[13]

2.1.2 지상관측소 자료

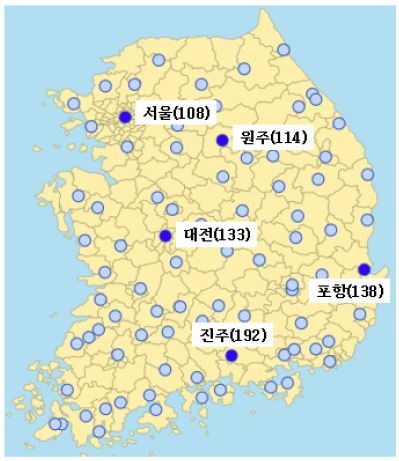
본 연구에서는 기상청에서 운용하는 지상관측소 중 지리적 분포를 고려한 총 5개 지점(서울, 원주, 대전, 포항, 진주)에서 취득된 일사량 데이터를 참조자료로 활용하였다(Fig. 2).

지상관측소의 일사량 자료는 시간 단위로 취득되는데, 청천일사량을 파악하기 위하여 천리안 위성의 가시영상에서 구름이 없는 맑은 날 특정 시간대의 값을 사용하였다. 일사량 자료는 천리안 위성 영상자료와 동일시기에 취득하였으며, 구름이 많아 청명일 선정이 어려운 달(4월, 6월~8월)을 제외하고 일사량이 가장 크게 나타나는 11시~2시사이의 자료를 분석하였다. 1월~11월 사이 6개 지점에 대한 월 평균 청명일은 약 4일로 나타났다.

Fig. 2.

Observation sites (parenthesis represents site codes)

2.2 실험 방법

본 연구에서는 천리안 기상위성의 영상자료로부터 TL을 계산하며, 청천일 모델을 통하여 청천일사량을 추정한다. 제안기법의 정확도 및 활용성을 분석하기 위하여 지상관측소에서 취득된 일사량을 참조자료로 하여 제안기법의 TL과 SoDa에서 제공하는 기존의 TL을 사용하여 계산된 각각의 청천일사량의 지점 및 월별 rRMSE와 rMBE를 비교하였다.

2.2.1 대기혼탁인자

본 연구에서는 AOD와 TPW, Angstrom 지수 α, β를 이용하여 특정 시간대에 따른 TL 계산하였다(식 (1)).^[13] Angstrom β변수는 AOD와 파장정보를 통하여 계산할 수 있다(식 (2)).^[13]α변수의 경우, 두 파장대에서 측정된 AOD를 이용하여 계산할 수 있으나(식 (3)),^[13] 파악 가능한 파장영역이 한 가지일 경우 1.3의 값으로 대체할 수 있다.^[13] 기상청에서 제공하는 에어로졸 광학두께의 경우 676nm에서 측정된 값을 사용하기 때문에 본 연구에서는 α의 값을 1.3으로 사용하였다.

$\[ \mathit{TL}=\left(1.8494+0.2425\times w-0.0203\times w^2\right)+\left(15.427+0.3153\times w-0.0254\times w^2\right)\times \beta \]$

(1)

$\[ \beta =\frac{{\tau }_{\alpha }\lambda }{{\lambda }^{-\alpha }} \]$

(2)

$\[ \alpha =\frac{\mathit{log}\left({\tau }_{\mathit{\alpha \lambda }2}/{\tau }_{\mathit{\alpha \lambda }1}\right)}{\mathit{log}\left({\lambda }_1/{\lambda }_2\right)} \]$

(3)

2.2.2 청천일사량

청천일사량은 청천일 모델로부터 계산된다. 청천일 모델은 입력변수와 대상지역에 따라 다양한 모델이 존재한다. ESRA(1999)는 대표적인 청천일 모델로, 유럽의 기상위성 Meteosat을 활용하여 일사량을 추정하는 Heliosat project 등에 사용되는 대표적인 모델이다.^[15] ESRA의 경우 대기 중 레일리산란을 제외한 기타 감쇠요소를 TL변수로 통합하여 고려하기 때문에 다양한 기상요소의 실측치를 고려하기 어려운 상황에서 위성영상에서 추출된 정보를 활용하여 청천일사량을 추정하기 용이하다.^[2] 따라서 위성영상을 이용해 청천일사량을 추정하는 기존의 다양한 선행연구에서 적용되고 있다.^[6,16]

ESRA에서 추정된 전일사량은 직달일사량과 산란일사량(diffuse irradiance)의 합으로 나타난다(식 (4)).

$\[ G=B+D \]$

(4)

1) 직달일사량

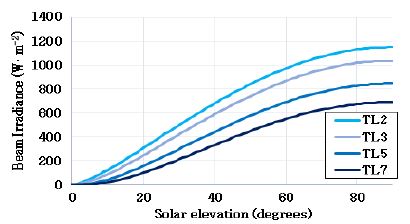
직달일사량이란 대기를 투과하여 지표면에 직접적으로 도달하는 일사량을 뜻하며, 식 (5)로 정의된다. 일반적으로 구름이 없고 부유물질이 적은 맑은 하늘일수록, 지표면으로 투과하는 일사량이 증가하기 때문에 모든 조건이 동일할 때, TL이 낮은 값을 가질수록 직달일사량이 증가한다.^[17]Fig. 3은 TL값이 2~7까지 변화할 때, 태양고도에 따른 직달일사량의 변화를 보여준다. 태양고도가 높아질수록 직달일사량이 증가하며, TL값이 큰 값을 가질수록 직달일사량이 감소하는 것을 확인할 수 있다.

Fig. 3.

Beam irradiance for the clear sky using different Linke turbidity values

$\[ B=I_0\epsilon \sin {\gamma }_s\mathit{exp}\left(-0.8862\mathit{TLm}{\delta }_R\left(m\right)\right) \]$

(5)

2) 산란일사량

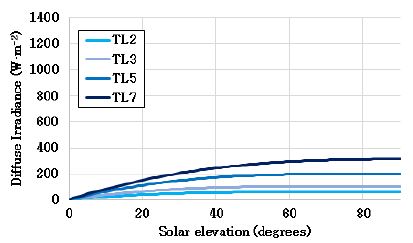
대기 중 에어로졸, 수증기 등의 부유물질이 많을수록 태양광의 산란이 많이 일어난다. 이러한 대기입자로 인하여 산란되어 지표면에 도달하는 일사량을 산란일사량이라고 하며 직달일사량과 반대로 TL이 커질수록 산란일사량이 증가한다(Fig. 4). ESRA모델에서 산란일사량은 산란 투과함수(diffuse transmittance function, T_rd)와 산란각도 함수(diffuse angular function, F_rd)로 정의 된다(식 (6)). 청천일사량은 맑은 날을 의미하기 때문에 T_rd은 상대적으로 낮은값을 가지며(식 (7)), F_rd은 태양고도와 TL에 따른 변수 A₀, A₁, A₂에 의해 결정된다(식 (8)~(9)).

Fig. 4.

Diffuse irradiance for the clear sky using different Linke turbidity values

$\[ D=I_0\epsilon T_{\mathit{rd}}\left(\mathit{TL}\right)F_d\left({\gamma }_s\mathit{TL}\right) \]$

(6)

$\[ T_{\mathit{rd}}\left(\mathit{TL}\right)=-1.5843\times {10}^{-2}+3.0543\times {10}^{-2}\mathit{TL}+3.797\times {10}^{-}{\left[\mathit{TL}\right]}^2 \]$

(7)

$\[ F_d\left({\gamma }_s,\mathit{TL}\right)=A_0+A_1\mathit{sin}\left({\gamma }_s\right)+A_2{\left[\mathit{sin}\left({\gamma }_s\right)\right]}^2 \]$

(8)

$\[ \begin{array}{c}{A}_0=2.6463\times {10}^{-1}-{6.158110}^{-2}\mathit{TL}+3.1408\times {10}^{-3}{\left[\mathit{TL}\right]}^2\\ A_1=2.0402+1.8945\times {10}^{-2}\mathit{TL}-1.1161\times {10}^{-2}{\left[\mathit{TL}\right]}^2\\ A_2=-1.3025+3.9231\times {10}^{-2}\mathit{TL}+8.5079\times {10}^{-3}{\left[\mathit{TL}\right]}^2\end{array} \]$

(9)

2.2.3 정확도 평가

천리안 기상자료를 활용하여 계산된 TL과 SoDa의 TL을 사용하여 계산된 청천일사량의 정확도를 평가하기 위하여 추정치와 실측치 간의 rRMSE와 rMBE를 분석하였다. 본 연구에서는 상대오차 개념을 포함하는 rRMSE와 rMEB를 사용하였으며, 각각 식 (10)과 (11)로 정의된다.^[18] rRMSE를 이용하여 추정치의 전체 정확도를 분석하였으며, rMBE값을 분석하여 추정치의 과/소 추정 여부를 평가하였다. rMBE의 경우, 0에 가까울수록 추정치와 실측치가 일치함을 나타내며, 양의 값일 경우 추정치가 실측치보다 과대추정 되었음을 의미한다.

$\[ rRMSE=\frac{\sqrt{\frac{1}{N}{\sum _{t=1}^N\left(\widehat{I}\left(t\right)-I\left(t\right)\right)}^2}}{\frac{1}{N}\sum _{t=1}^{N}I\left(t\right)} \]$

(10)

$\[ rRMSE=\frac{\frac{1}{N}\sum _{t=1}^N\left(\widehat{I}\left(t\right)-I\left(t\right)\right)}{\frac{1}{N}\sum _{t=1}^{N}I\left(t\right)} \]$

(11)

3. 실험 결과

3.1 TL 계산 결과

Fig. 5는 각 지점별로 천리안 위성 자료를 통해 산출된 TL(COMS_TL)과 SoDa에서 제공한 TL(SoDa_TL)의 월평균 값을 나타낸 것이다. SoDa_TL의 경우 기후 평균값을 나타내기 때문에 COMS_TL에 비해 상대적으로 낮은 값을 갖는다. 또한 SoDa_TL은 5월과 9월에 가장 높은 값을 갖는 특징을 보이며 지역별 차이가 두드러지지 않는 반면, COMS_TL은 측정 지점별로 차이를 보이고 있으며, 3월에 가장 낮고 9월에 가장 높은 값을 가졌다.

Fig. 5.

Monthly TL values for observation sites

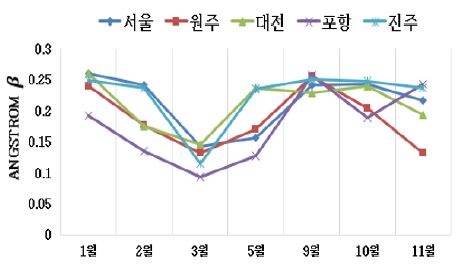
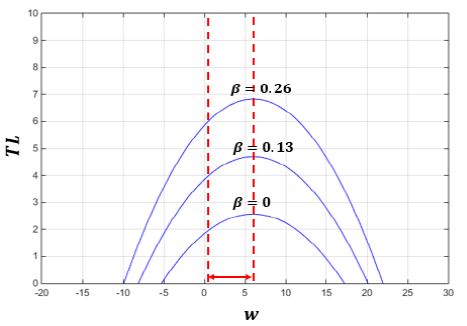
COMS_TL을 계산하기 위하여 사용된 Angstrom β변수와 TPW 인자의 영향을 분석하기 위하여 지점별 월평균값을 비교하였다(Fig. 6~7). TPW은 모든 지점에서 유사한 경향을 보이며, 1월부터 점차 증가하다 9월에 가장 높은 값을 갖고 다시 감소한다. 반면 β변수는 지점별로 차이를 보이지만, 공통적으로 3월에 가장 낮은 값을 갖는다. COMS_TL의 경우 β변수의 월평균값의 변화와 유사한 경향을 나타내는데, 이는 식 (1)에 따라 TL값이 TPW보다 β변수에 의해 급격히 변화하기 때문으로 보인다. 일반적으로 TPW와 β변수는 0.5≤w≤6, 0≤β≤0.26의 범위에서 정의되며,^[13] TL의 변화폭은 TPW보다 β변수에 의해 커지는 것을 알 수 있다(Fig. 8).

Fig. 6.

Monthly precipitable water values

Fig. 7.

Monthly Angstrom β values

Fig. 8.

values according to w and β

Angstrom β변수는 에어로졸의 양 뿐 만 아니라 크기와 입자 분포의 영향을 받기 때문에, β변수값의 차이는 청명일로 선정한 해당 일자와 시간대에 따른 에어로졸의 종류와 분포의 광학특성의 차이로 설명할 수 있다.

3.2 청천일사량 계산 결과

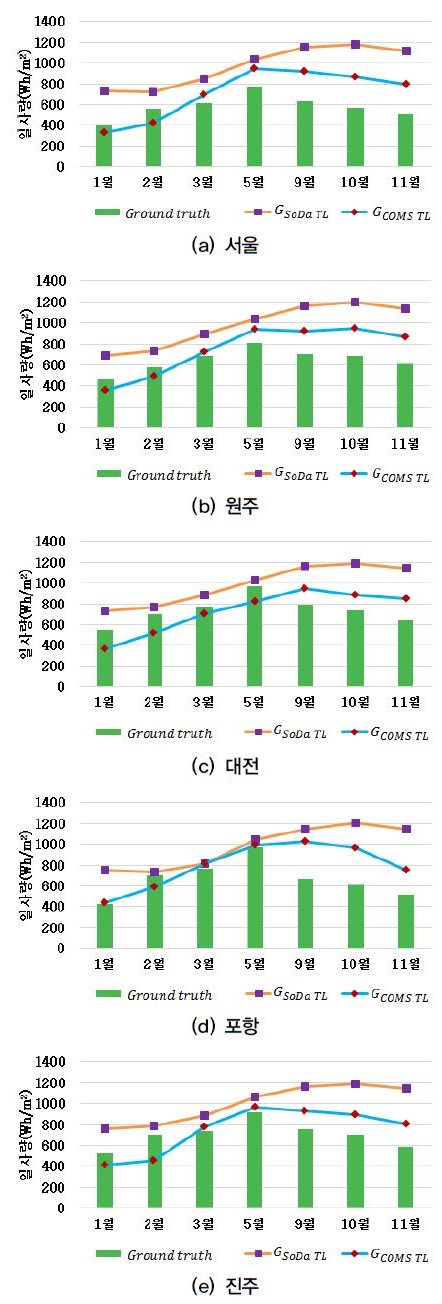
COMS_TL과 SoDa_TL을 각각 ESRA모델에 적용하여 청천일사량을 산출하였으며, 월평균 값을 실측치와 비교한 결과는 Fig. 9와 같다.

Fig. 9.

Comparison of the monthly clear sky irradiance

전반적으로 월평균 G_COMSTL가 G_{So Da TL}보다 낮은 값을 가졌으며, 이는 COMS_TL 자체가 기후평균값을 사용하는 SoDa_TL보다 높기 때문이다(Fig. 5).

G_{So Da TL}는 모든 지점과 시기에 대하여 실측치에 비해 과대추정하는 경향을 보인다. 특히 이러한 현상은 9~11월에 두드러지는데, 이 시기에 지상관측소에서 측정한 일사량은 감소하는 반면 G_{So Da TL}는 오히려 증가하거나 정체하여 rRMSE와 rMBE가 큰 값을 가졌다(Table 1).

Table 1.

Monthly rRMSE and rMBE

반면, G_COMSTL도 9~11월에 일사량을 과대추정 하였으나 실측치와 동일하게 감소하는 경향을 보였으며, G_{So Da TL}에 비해 실측치와 가까운 값을 가졌다. 실제로 이 시기의 5개의 모든 관측지점에서 G_COMSTL의 rRMSE와 rMBE가 G_{So Da TL}보다 낮은 값을 갖는다.

1~5월 사이에는 G_{So Da TL}와 G_COMSTL가 비교적 실측치와 가까운 값을 갖기 때문에 9~11월에 비해 rRMSE가 낮다. 전반적으로 G_COMSTL의 rRMSE가 G_{So Da TL}보다 낮으나, 1~2월에는 G_COMSTL가 실측치를 과소추정하는 경향을 보인다. 실제로 5개 지점에서 2월의 rMBE는 음의 값을 보이며, 진주에서 가장 큰 값을 갖는다.

ESRA모델을 적용하여 청천일사량을 계산할 때, 다른 입력 조건이 동일한 상태이기 때문에 rRMSE와 rMBE는 COMS_TL과 SoDa_TL이 실제 한반도 대기를 얼마나 적절하게 반영하였는지 판단할 수 있는 기준이 될 수 있다. 따라서 rRMSE의 감소가 두드러지는 9~11월을 포함하여 전반적으로 COMS_TL이 한반도의 대기 상황을 잘 반영한 것으로 보이며 3월과 5월에 정확도가 가장 높다고 할 수 있다. 반면 2월의 경우 포항과 진주 등의 지점에서 G_COMSTL의 rRMSE가 크고 rMBE가 음의 값을 갖는 것으로 보아 COMS_TL보다 SoDa_TL값이 실제 대기상태를 잘 반영한 것으로 보인다.

4. 결론 및 연구과제

본 연구에서는 위성영상으로부터 한반도 지역의 일사량을 추정하기 위하여 대기 상태를 반영하는 중요한 인자인 TL을 천리안 위성의 영상 자료를 활용하여 직접 계산하였으며, 이의 활용 가능성을 평가하기 위하여 기존 SoDa에서 제공하는 TL자료와 비교하였다. 또한 각각의 TL값들을 사용하여 청천일사량을 구하였으며, 지상에서 취득된 일사량을 사용하여 정확도 평가를 수행하였다.

전반적으로 COMS_TL이 기후평균값을 사용하는 SoDa_TL보다 높은 값을 가졌으며, G_COMSTL가 G_{So Da TL}보다 실측치에 가까운 일사량을 나타냈다. G_COMSTL는 1~5월 사이 rRMSE가 낮았으며 9~11월에 G_{So Da TL}가 일사량을 과대추정하는 경향을 개선할 수 있었다.

본 연구의 한계로는 청명일을 선정하기 어려운 달의 결과는 평가할 수 없었으며, 한 달에 2~4일의 청명일을 실험하였기 때문에 선정된 청명일의 특징에 따라 월평균값이 편향된 결과가 도출될 수 있다는 문제가 있다. 또한 제공된 천리안 위성의 AOD와 TPW의 경우, 취득된 시간대의 구름의 영향에 따라 null값을 갖는 경우가 있는데 이러한 경우에는 값을 파악하기 힘들기 때문에 TL값 뿐 만 아니라 청천일사량 계산에 오차를 불러올 수 있다. 따라서 전처리 과정에서 청명일을 보다 정확히 구분할 수 있는 구체적인 기준을 추가하여 계산된 TL 및 청천일사량의 대한 보다 정확한 평가가 이루어 질 수 있도록 추가 연구를 수행할 예정이다.

Acknowledgments

본 연구는 한국에너지기술연구원의 주요사업으로 수행한 결과입니다(B6-2427).

References

• 이정호, 최원석, 김용일, 윤창열, 조덕기, 강용혁, (2013), “천리안 기상영상기 영상을 이용한 한반도 지역의 수평면 전일사량 추정”, 대한원격탐사학회지, 29(1), p151-160.
• Polo, J., Antonanzas-Torres, F., Vindel, J.M., Ramirez, L., (2014), “Sensitivity of satellite-based methods for deriving solar radiation to different choice of aerosol input and models”, Renewable Energy, 68, p785-792. [https://doi.org/10.1016/j.renene.2014.03.022]
• Jia, B., Xie, Z., Dai, A., Shi, C., Chen, F., (2013), “Evaluation of satellite and reanalysis products of downward surface solar radiation over East Asia: Spatial and seasonal variations”, Journal of Geophysical Research: Atmospheres, 118(9), p3431-3446. [https://doi.org/10.1002/jgrd.50353]
• Blanc, P., Gschiwind, B., Lefevre, M., Wald, L., (2011), “The HelioClim Project: Surface Solar Irradiance Data for Climate Applications”, Remote Sensing, 3, p343-361. [https://doi.org/10.3390/rs3020343]
• Rigollier, C., Bauer, O., Wald, L., (2000), “On the clear sky model of the ESRA – European Solar Radisation Atlas with respect to the Heliosat method”, Solar Energy, Elservier, 68(1), p33-48.
• Hove, T., Manyumbu, E., (2013), “Estimates of the Linke turbidity factor over Zimbabwe using ground-measured clear-sky global solar radiation and sunshine records based on a modified ESRA clear-sky model approach”, 52, p190-196. [https://doi.org/10.1016/j.renene.2012.09.059]
• Fontoynont, M., Dumortier, D., Heinnemann, D., Hammer, A., Olseth, J., Skarveit, A., Beyer, H. G., (1998), “Satellight: a WWW server which provides high quality daylight and solar radiation data for Western and Central Europe”, In 9th Conference on Satellite Meteorology and Oceanography, Paris, (No.2), p434-437.
• SoDa, (2016), Solar Energy Services for Professtionals, <www.soda-is.com/eng/index.html>.
• Šúri, M., Jaroslav, H., (2004), “A new GIS‐based solar radiation model and its application to photovoltaic assessments”, Transactions in GIS, 8(2), p175-190. [https://doi.org/10.1111/j.1467-9671.2004.00174.x]
• Nou, J., Chauvin, R., Thil, S., Eynard, J., Grieu, S., (2015), “Clear sky irradiance model for real-time sky imager application”, Energy Procedia, 69, p1999-2008. [https://doi.org/10.1016/j.egypro.2015.03.208]
• Mavromatakis, F., Franghiadakis, Y., (2007), “Direct and indirect determination of the Linke turbidity coefficient”, Solar Energy, 81, p896-903. [https://doi.org/10.1016/j.solener.2006.11.010]
• Chaâbane, M., Masmoudi, M., Medhioub, K., (2004), “Determination of Linke turbidity factor from solar radiation measurement in northern Tunisia”, Renewable energy, 29, p2065-2076. [https://doi.org/10.1016/j.renene.2004.03.002]
• Remund, J., Wald, L., Lefèvre, M., Ranchin, T., Page, J., (2003), “Worldwide Linke turbidity information”, In ISES Solar World Congress 2003, International Solar Energy Society (ISES), 400, p13.
• 기상청, (2015), “예보관 훈련 기술서(위성 기상학)”, http://web.kma.go.kr/communication/elearning/fct_trn_2.jsp.
• ESRA, (1999), “European solar radiation atlas”, Fourth edition, include. CD-ROM, Edited by J. Grief, K. Scharmer, Scientific advisors: R. Dogniaux, J. K. Page, Authors: L. Wald, M. Albuisson, G. Czeplak, B. Bourges, R. Aguiar, H. Lund, A. Joukoff, U. Terzenbach, H.G. Beyer, E.P. Borisenko, Published for the Commission of the European Communities by Presses de 1’Ecole, Ecole des Mines de Paris, Paris, France.
• Hoff, T. E., Perez, R., Kleissl, J., Renne, D., Stein, J., (2013), “Reporting of irradiance modeling relative prediction errors”, In Progress in Photovoltaics: Research and Applications, 21(7), p1514-1519. [https://doi.org/10.1002/pip.2225]
• 송아람, 최원석, 윤창열, 김용일, (2015), “한반도의 일사량 추정을 위한 청천일 모델의 비교평가”, 한국측량학회지, 33(5), p415-426.
• Inman, R.H., Pedro, H.T.C., Coimbra, C.F.M., (2013), “Solar forecasting methods for renewable energy integration”, Proceeding of Energy Combust. Sci, 39(6), p535-576. [https://doi.org/10.1016/j.pecs.2013.06.002]