알카라인 수전해 시스템 대상 온도와 압력 동시 제어 조건의 수소 생산 특성 평가

1. 서 론

탄소 배출량 저감을 위해 기존 화석 연료에서 무탄소 연료로 전환되면서 수소의 생산 및 활용 기술 개발의 중요성이 증대되고 있다. 수소는 기존 화석 연료 대비 발열량이 높은 특징을 가지고 있다.^[1~3] 수소는 생산 방식에 따라 그레이 수소, 블루 수소, 청록 수소, 핑크 수소, 옐로우 수소, 그린 수소 등으로 분류된다. 그레이 수소는 석유화학이나 제철 공정에서 부산물로 생성되는 부생 수소와 천연가스나 석탄과 같은 화석 연료의 개질을 통해 생산되는 수소이다. 화석 연료의 활용으로 인해 이산화탄소(CO₂)가 배출되며 탄소 포집(Carbon Capture & Storage, CCS)이 포함되는 수소를 블루 수소라 통칭한다.^[4] 청록 수소는 천연가스의 열분해를 통해 수소와 고체탄소를 동시에 생산하는 기술이다. 핑크, 엘로우, 그린 수소는 수전해를 통해 생산되는 수소이다. 핑크 수소는 원자력과 수전해 시스템을 연계하여 수소를 생산하는 방식이며 옐로우 수소는 기존 중앙 전력을 통해 수전해를 기반으로 생산되는 방식이다. 그린 수소는 신재생에너지를 통해 생산되는 전기를 기반으로 수전해를 통한 수소 생산 기술이다. 그린 수소는 다른 수전해 기반의 수소생산 방식들 보다 이산화탄소 배출량이 낮은 청정 수소 생산방식이지만 신재생에너지원의 간헐성 문제가 안정적인 수소생산 및 수전해시스템 운영에 한계로 남아있다. 신재생에너지원의 간헐성 극복을 위한 에너지저장시스템(Energy Storage System, ESS)을 도입하고 있지만 화재 및 운영의 문제로 인해 적극적인 활용이 어려운 실정이다. 신재생에너지원과 수전해의 연계 운전을 위해서는 수전해 시스템의 가변 운전(부하 변동) 기술 개발이 필요하다.^[5,6]

수전해는 물을 전기 분해하여 수소와 산소를 생산하는 기술이다. 물에 전기 에너지를 가하면 산소는 음이온으로 수소는 양이온의 형태로 분해되어 분리막을 통해 양극으로 분리되어 (+)극에는 산소가 발생하고 (-)극에는 수소가 발생한다.^[7] 수전해 기술은 고분자전해질막 수전해(Polymer Electrolyte Membrane Water Electrol-ysis, PEM), 고체산화물 수전해(Solid Oxide Electrolysis Cell, SOEC), 음이온 교환막 수전해(Anion Exchange Membrane, AEM), 알칼라인 수전해(Alkaline Water Electolysis, AWE)로 분류된다.^[8] PEM 수전해는 높은 전류밀도를 형성하며 가볍고 부피가 작은 기기 특성과 높은 순도의 수소를 안정적으로 생산가능하다는 장점이 있다. 하지만 백금과 같은 귀금속을 촉매로 사용하여 알칼라인 수전해에 비해 촉매의 가격 경쟁력이 낮다는 단점이 존재한다.^[9,10] SOEC는 700~900°C 고온에서 작동하기 때문에 저렴한 촉매를 사용할 수 있다는 장점이 있지만^[11] 고온의 열원에 대한 에너지 비용이 한계로 사업장 폐열활용과 같은 방법으로 운영될 수 있다. 또한 고온의 운전조건에서 내구성이 좋은 재료를 사용하는데 가격상승의 요인이 있다. AWE는 60~70°C의 저온에서 운전이 가능하며 촉매의 가격 경쟁력 확보가 가능하여 대규모 수소 생산 장치로 활용이 가능한 장점을 가진다. 하지만, 다른 수전해 기술에 비해 낮은 전류밀도로 인해 단일 셀 규모에서 수소 생산량이 낮은 단점을 가진다.^[12] AWE는 고효율의 전극과 맴브레인 등 신소재 개발과 운영 최적화를 위한 기술이 개발중이다. AWE 시스템은 작동 온도와 압력 조건에 따라 생산량과 효율이 달라진다. 수전해에서 온도의 제어는 셀전압과 전류밀도에 직접적인 영향을 준다. 최근 AWE 관련 선행 연구에서는 각각의 압력 변화 조건과 온도 변화 조건에서 수소 생산 특성과 운전 영향 평가를 중점에 두고 연구를 수행하였다.^[13~15] 수전해 시스템에서 제어 가능한 주요 변수는 압력과 온도이며 부하 변동에 대응하기 위해 두 변수를 동시에 제어하는 연구 개발이 필요하다. AWE는 스택의 작동 압력 대비 온도의 영향이 크게 나타난다.^[15] 알카라인 수전해 시스템의 부하 변동 대응 위해 변동 시간이 긴 온도 제어보다 압력 제어가 이점이 있다. AWE의 최적 운영을 위해서는 압력과 온도를 동시 제어가 필요하다. AWE 시스템은 낮은 전류밀도에서 셀전압이 급격히 증가하며 높은 전류밀도에서는 셀전압이 완만히 증가하는 특성을 가지고 있다.^[16] 높은 부하 영역에서는 직선으로 전류 밀도가 변화되어 부하 변동이 비교적 용이하지만 낮은 부하에서 Exponetial 한 전류 밀도 변화로 인해 운전 예측 및 대응이 어려운 실정이다. 따라서, 낮은 부하 영역에서 온도와 압력에 따른 수전해 시스템의 운전 해석 및 예측이 필요하다.

본 연구에서는 압력과 온도 2가지의 변수를 기반으로 AWE 시스템의 운전과 상관관계 조사했으며 10-90%의 부하변동 조건에서 수소 생산 특성 및 시스템 운영 특성을 분석했다. AWE 시스템은 스택과 BOP(Balance of Plant)를 대상으로 수치해석과 공정해석을 진행하였다. 부하별 수소 생산량을 동일하게 유지한 후 1차로 압력 조절을 통해 부하 대응을 위한 영향을 분석하였다. 2차로 온도 제어 조건을 고려하여 해석을 수행하여 압력과 온도를 동시 제어해서 부하 변동 가능 범위를 모색하였다.

2. 연구방법

2.1 알카라인 수전해 시스템 구성

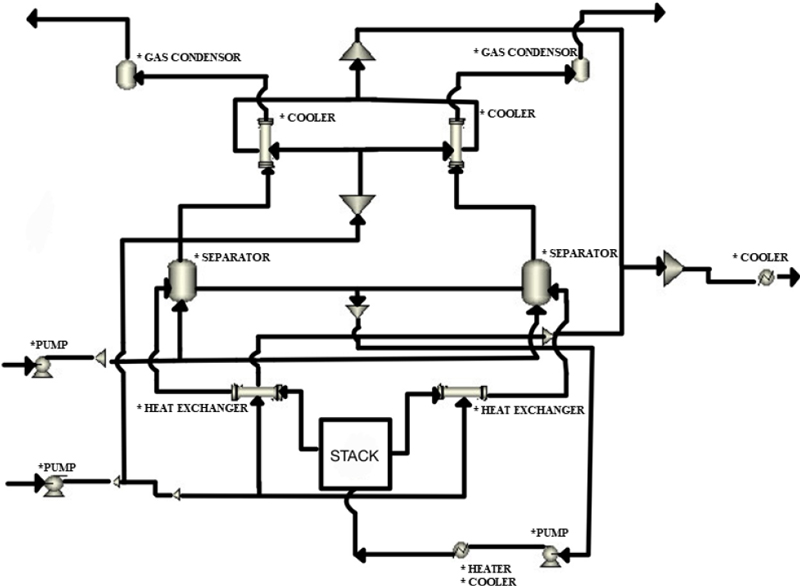
Fig. 1은 본 연구의 대상 알카라인 수전해 시스템의 개략도에 대해 나타낸 것이다. 알카라인 수전해 시스템은 스택(Stack), 열교환기(Heat Exchanger), 기수분리기(Seperator), 냉각기(Cooler), 응축기(Gas Condensor), 펌프(Pump) 등으로 구성된다. 스택에서는 수전해 반응을 통해 수소와 산소가 생산되며 반응하지 않은 물과 전해질(KOH)이 배출된다. 스택과 연결된 열교환기는 수전해 반응을 통해 온도가 상승한 수소, 산소, 물과 전해질의 온도를 낮춘다. 기수분리기는 액체(물, 전해질)와 기체(수소, 산소)를 분리하게 되며 액체 물질은 스택으로 순환된다. 기체는 냉각기를 통해 온도가 낮아진 후 응축기를 통해 최종 수소와 산소를 생산하게 된다. 시스템에서 액체와 기체 물질은 펌프를 통해 각 시스템의 목표 압력으로 제어되어 흐르게 된다.

Fig. 1.

Schematic diagram of Alkaline Water Electrolysis (AWE) system

2.2 수치해석 모델링 방법 및 조건

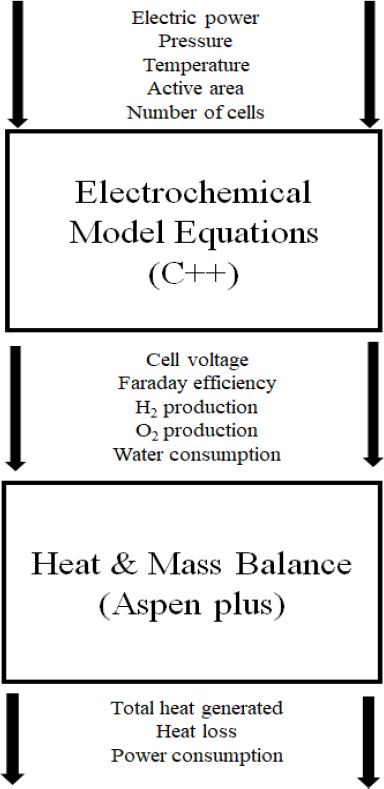
본 연구에서 알카라인 수전해의 모델링은 수치해석과 공정해석을 동시에 수행하였다. Fig. 2는 알카라인 수전해 시스템의 해석 메커니즘을 나타낸 것이다. 수전해 시스템의 해석은 정상상태 조건으로 수행되었다. 수전해 시스템의 스택은 C⁺⁺ 기반의 전기화학 모델을 통해 셀 전압, 패러데이 효율, 수소/산소 생산량, 물 소비량을 계산하였다. BOP 해석은 상용 해석 Tool인 Aspen⁺를 통해 공정해석을 수행하였다. 공정해석은 각각의 BOP 시스템의 Heat & Mass balance를 기반으로 물질의 온도, 압력과 전력 소모량을 계산한다.

Fig. 2.

Process flow of numerical analyses of AWE stack and Balance of Plant (BOP)

2.2.1 스택 해석 방법

스택에서 수소, 산소 생산 메커니즘은 아래 식 (1)~(3)에 나타나 있다. 스택의 음극에서는 식 (1)과 같이 수소가 생성되는 HER(Hydrogen Evolution Reaction) 반응이 일어난다. 양극에서는 식 (2)와 같이 전해질로 사용되는 알카라인 수용액을 통해 OH- 가 전달되어 생산되는 OER(Oxygen Evolution Reaction)통해 산소가 생산된다. 식 (3)은 스택의 총 반응식으로 양 전극 사이에서 에너지를 투입하여 물의 전기 분해를 통해 수소와 산소가 생성되는 기본 메커니즘을 나타낸 것이다.^[17,18]

$\[ 2H_{2}O\left(l\right)+2e^{-}\to H_2\left(g\right)+2{OH}^{-}\left(aq\right) \]$

(1)

$\[ 2{OH}^{-}\left(aq\right)\to \frac{1}{2}{O}_2\left(g\right)+H_{2}O\left(l\right)+2e^{-} \]$

(2)

$\[ H_{2}O\left(l\right)+ Energy \to H_2\left(g\right)+\frac{1}{2}{O}_2\left(g\right) \]$

(3)

수전해 시스템에 필요 에너지(Input Power, W_stack)는 식 (4)와 같이 전압과 전류의 상관관계식으로 계산되다.^[13]

$\[ W_{stack }=V_{cell }\bullet n_{cell }\bullet j_{cell }\bullet A \]$

(4)

식 (4)에서 셀전압(V_cell)은 두전극 사이에서 발생하는 전압(전위차, Voltage)이며 n_cell은 스택에 설치된 셀의 수(Number), j_cell은 전극에서 생성되는 전류를 활성화면적으로 나누어 단위면적당 흐르는 전류를 의미하는 전류밀도(Current Density, A/cm²)이다. A는 전극의 표면 중 전기화학 반응이 일어난 활성화면적(Active Area)을 나타낸다.

스택의 전류밀도는 전극 사이의 전위차인 V_cell을 기반으로 계산되며 식 (5)에 상관관계식을 나타내었다.^[17]

$\[ V_{cell =}{E}_{rev }+V_{\left(act-c-\theta \right)}+V_{\left(act-a-\theta \right)}+V_{ohm}+V_{diff } \]$

(5)

V_cell은 E_rev(가역전압), V_act(활성화과전압), V_Ω(저항에 의한 과전압), V_diff(확산에 의한 과전압)로 구성된다. 수전해의 생성물로 양극에서 생성되는 수소와 산소 기체는 분리막에 의해 혼합이 거의 일어나지지 않기에 확산에 의한 영향이 매우 적어 계산에서 제외하였다.^[14]

$\[ \begin{array}{c}{E}_{rev }=E_{rev }^{\circ }+\frac{RT}{2F}ln\left[\frac{{\left(P-P_{H2O}\right)}^{1.5}{P}_{H2O}^{*}}{P_{H2O}}\right]\\ E_{rev }^{\circ }\left(T\right)=1.50342-9.956\times {10}^{\left(-4\right)}T\\ +2.5\times {10}^{\left(-7\right)}{T}^2\end{array} \]$

(6)

가역전위(E_rev)는 식 (6)과 같이 계산되며 반응물과 생성물의 activity, 온도, 압력에 영향을 받는다.

$\[ P_{H_{2}O}^{*}=T^{\left(-3.498\right)}exp\left(37.93-\frac{6426.32}{T}\right) \]$

(7)

$\[ \begin{array}{c}{P}_{H2O}=T^{\left(-3.498\right)}exp\left(37.93-\frac{6426.32}{T}\right)\\ \times exp\left(0.016214-0.13082m+0.1933m^{0.5}\right)\end{array} \]$

(8)

반응물인 물(H₂O)의 표준상태에서의 압력을 의미하는 P^*_H2O은 식 (7), 온도에 따른 물의 부분압(P_H2O)은 식 (8)과 같이 온도와 전해질 농도(molarity, m) 모두의 영향을 받는다. 전해질 농도의 영향은 식 (8)과 같다.^[14,19,20]

$\[ V_{act}=\frac{RT}{F{\alpha }_a}{sinh}^{-1}\left(\frac{j}{j_{o,a}}\right)+\frac{RT}{F{\alpha }_c}{sinh}^{-1}\left(\frac{j}{j_{o,c}}\right) \]$

(9)

$\[ j_{0,c}=1.5\times {10}^{-4}{\left(\frac{P}{P_{ref}}\right)}^{0.1}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{23000}{RT}\left(1-\frac{T}{T_{ref}}\right)\right] \]$

(10)

$\[ j_{0,a}=0.9\times {10}^{-4}{\left(\frac{P}{P_{ref}}\right)}^{0.1}\mathrm{e}\mathrm{x}\mathrm{p}\left[-\frac{42000}{RT}\left(1-\frac{T}{T_{ref }}\right)\right] \]$

(11)

$\[ {\alpha }_a=0.07835+0.001T \]$

(12)

$\[ {\alpha }_c=0.1175+0.00095T \]$

(13)

활성화과전압(V_act)은 전기화학반응이 평형상태를 벗어나 반응이 진행될 수 있도록 하는데 소모되는 전압을 의미하며, 식 (9)과 같이 계산된다. 음극과 양극 사이에서 발생하는 교환 전류밀도(j_0,c/j_0,a)는 스택에 사용되는 전극의 주요 소재인 니켈(Ni)에 관련한 선행 연구 결과를 참고하여 식 (10)과 식 (11)로 계산하였다. 위의 식에서 α_a와 α_c는 양극과 음극의 전하전달 계수를 나타낸 것이다. 양 극에는 니켈 소재가 사용되어 식 (12)와 (13)을 사용하였다.^[14,20,21]

$\[ S_{available }=S\cdot \left(1-\theta \right) \]$

(14)

$\[ \theta =0.023{\left(j\right)}^{0.3}{\left(\frac{T}{T_{ref}}\frac{P_{ref}}{P}\right)}^{\frac{2}{3}} \]$

(15)

$\[ \begin{array}{c}{V}_{act}=\frac{RT}{F{\alpha }_a}{sinh}^{-1}\left(\frac{i}{j_{o,a}\cdot S\cdot \left(1-\theta \right)}\right)\\ +\frac{RT}{F{\alpha }_c}{sinh}^{-1}\left(\frac{i}{j_{o,c}\cdot S\cdot \left(1-\theta \right)}\right)\end{array} \]$

(16)

수전해 반응 중 생성되는 기포는 활성화 면적을 감소시키며 이를 버블 효과(Bubble Effect)라 통칭한다. 버블 효과를 보정한 활성화면적(S_available)은 식 (14)와 같이 구해진다. 기포에 의해 가려지는 면적의 비율을 θ로 표현하였으며, 그 비율을 계산하는 방법은 식 (15)와 같다. 버블 효과를 고려한 식 (9)의 활성화과전압을 식 (16)과 같이 변경하여 사용할 수 있다.^[14,21]

$\[ V_{\Omega }=I\times \left(R_{cathode }+R_{Anode }+R_{KOH }+R_{mem }\right) \]$

(17)

저항에 의한 과전압(V_ohm)은 식 (17)과 같이 전류와 전체 저항을 기반으로 계산된다. 저항에 의한 과전압은 양 전극, 전해질과 분리막(Membrane)에서 발생하는 저항을 고려한다.^[13]

$\[ R_{cathode/anode }=\frac{1}{{\sigma }_{cathode/anode }}\left(\frac{L}{S}\right) \]$

(18)

$\[ \begin{array}{l}{\sigma }_c={\sigma }_a={\sigma }_{Ni}\\ =60000000-279650T+532T^2-0.38057T^3\end{array} \]$

(19)

전극에 의한 저항은 전극으로 사용되는 물질의 특성과 크기(두께와 면적)에 따라 다르며 특성은 식 (18)과 같다. L은 전극의 두께를, S는 활성화 면적을 의미하며, 활성화 면적을 계산할때는 식 (14)에서 묘사한 버블효과를 고려하여야 한다. σ는 물질의 전기전도도(Electrical Conductivity)이며, 양 전극은 모두 니켈로 구성되어 있다. 식 (19)와 같이 온도의 영향을 받으며 양 극에서 같은 값을 가진다.^[21]

$\[ \begin{array}{c}{\sigma }_{KOH}=-2.401m-0.0028m^2+0.005332mT\\ +207.2\frac{m}{T}+0.001043m^3-0.0000003m^2{T}^2\end{array} \]$

(20)

$\[ \frac{{\sigma }_{KOH-bubble}}{{\sigma }_{KOH}}={\left(1-ϵ\right)}^{\frac{3}{2}},\left[ϵ=\frac{2}{3}\theta \right] \]$

(21)

$\[ R_{KOH-Bubble}=\frac{1}{{\sigma }_{KOH}{\left(1-ϵ\right)}^{1.2}}\left(\frac{d_{am}}{S_a}\frac{d_{cm}}{S{d}_c}\right) \]$

(22)

전해질로 사용되는 물질은 KOH이며 전해질의 전기전도도를 구하는 식은 식 (20)과 같고, 전해질에서 발생하는 저항은 식 (22)와 같다. 하지만, 전극에서 버블 효과의 영향을 받기 때문에 버블효과를 포함한 전해질의 저항을 Bruggeman Equation을 통해서 식 (21)과 같이 구할 수 있다.^[21] 전해질의 전도는 전극과 분리막 사이에 거리가 제로갭 형태로 이루어져 있을 경우에는 전해질에서 발생하는 저항의 값을 무시할 수 있어 셀전압을 감소시킬 수 있다.^[22]

$\[ R_{mem}=\frac{0.06+80e^{-\frac{T^{\text{'}}}{50}}}{10000S_{mem}} \]$

(23)

분리막(Membrane)에서 발생하는 저항은 선행 연구에서 인용하여 0.5 mm 두께를 가지는 Zirfon 분리막의 저항으로 식 (23)과 같이 사용하였다. S_mem은 분리막의 면적이고, T'은 온도(°C)이다.^[21]

패러데이 효율(Faraday Efficiency (η_F))은 이론적 수소 생산량과 실제 수소 생산량의 비이며, 전류밀도와 온도에 영향을 받는다. 수소 생산량은 패러데이 효율을 기반으로 계산된다.

$\[ \begin{array}{l}{\eta }_F=\frac{n_{H2, Stack }}{n_{H2,theoreical }}\\ =\left(\frac{j^2}{f_{11}+f_{12}*T+j^2}\right)*\left(f_{21}+f_{22}*T\right)\end{array} \]$

(24)

$\[ n_{H_2}={\eta }_F\frac{j_{cell }\bullet A}{2F}{n}_{cell } \]$

(25)

패러데이 효율은 식 (24)에 있는 매개변수 4개(f₁₁, f₁₂, f₂₁, f₂₂)와 전류밀도, 온도의 함수로 나타나며, 이 값을 식(25)에 사용하여 수소 생산량(n_H2)을 계산하였다. 매개변수의 값은 Table 1에 정리돼있다.^[15,23]

Table 1.

Fraday efficiency model of stack

2.2.2 알칼라인 수전해 스택 해석 조건

Table 2는 알카라인 수전해 스택의 수치해석 조건에 대해 나타낸 것이다. 스택 수치해석은 60-85°C의 온도 범위에서 5°C 간격으로 온도 변화에 따른 수전해 특성 분석을 수행하였다. 스택의 압력 조건은 1, 3, 5, 7, 10, 20, 30 bar이다. 대상 알카라인 수전해 시스템의 규모는 150 kW이며, 부하 변동 조건은 10, 30, 50, 70, 90%로 설정하여 수치해석을 수행하였다. 스택의 반응 면적은 0.785 m²이며 셀수는 32개, 전해질(KOH)의 농도는 30 wt.%이다. 온도 및 압력의 변동에 따른 수소 생산량의 변화를 비교하기 위해 일반적인 수전해 시스템의 작동 조건인 70°C, 7 bar 조건을 기준 조건으로 설정하였다.^[22]

Table 2.

Conditions of numerical analysis of stack

2.2.3 수전해 시스템 BOP 해석 방법 및 조건

수전해 시스템의 BOP 해석은 상용 Tool인 Aspen⁺를 사용하여 Fig. 1과 같이 열교환기(Heat Exchanger), 기수분리기(Seperator), 냉각기(Co-oler), 응축기(Gas Condensor), 펌프(Pump)로 구성하였다. BOP 해석은 스택의 수치해석을 통해 계산된 수소, 산소, 전해질, 물의 물질 상태량을 연계하여 공정해석을 수행하였다. Table 3은 BOP 시스템의 기기별 작동 조건에 대해 나타낸 것이다. 본 연구에서는 부하 변동 조건에서 스택의 압력과 온도에 대한 운전 특성을 분석하기 위해 스택의 압력 강하를 고려하였다. 스택에서 압력 강하는 각 압력 조건별 5%로 설정하여 해석을 수행하였다. 스택으로 투입되는 압력은 펌프를 통해 부하 및 압력별 압력 강하를 고려하여 투입되는 전력 소모량을 계산하였다. 스택에서 전기화학 반응으로 인해 물질(전해질, 물, 수소, 산소) 온도가 상승하게 되며 열교환기(Heat Exchanger)를 통해 스택으로 투입되는 전해질과 물의 온도를 1차 낮추게 된다. 본 연구에서는 스택 운전의 기준 조건(Reference Ca-se)은 7 bar, 70°C로 설정하였다. 부하별 해당 온도, 압력에서 생산되는 수소 생산량을 계산하였으며 스택에서 생산되는 수소 생산량을 고려하여 각각의 압력별 요구되는 작동 온도를 계산하였다. 부하 및 압력별 열교환기의 투입 온도는 56.9~67.8°C이며 출구온도는 65.7~73.3°C의 범위이다. 기수분리기는 물, 전해질의 액체와 수소, 산소의 기체를 분리하는 장치로써 열손실은 고려하지 않았다. 기수분리기에서 수소 및 산소와 함께 일부의 H₂O(Steam), N₂ 등의 가스도 함께 배출된다. 따라서 BOP 시스템에서는 냉각기와 응축기를 통해 온도를 낮추어 H₂O를 응축시키게 되며 수소와 산소의 순도를 증가시킨다. 냉각기 출구의 가스 온도는 55°C이며 응축기 출구의 25°C로 설정했다.^[24]

Table 3.

Conditions of process simulation of BOP

공정 해석을 통해 BOP 시스템의 요소 장치들의 열전달량을 계산했으며, 이를 통해 전력 소모량을 도출하였다. 열교환기들의 냉각수는 열전달을 통해 온도가 상승한 후 히트 펌프를 통해 냉각하여 각 시스템으로 재순환된다. 따라서 전력 소모량은 히트 펌프의 냉방 성능 계수(COP) 3으로 설정했다. 최종 BOP의 전력 소모량은 히트 펌프와 물/전해질 펌프의 전력 소모량을 고려하여 산정했다.

3. 연구 결과 및 고찰

3.1 부하, 온도, 압력에 따른 스택의 운전 특성 분석 결과

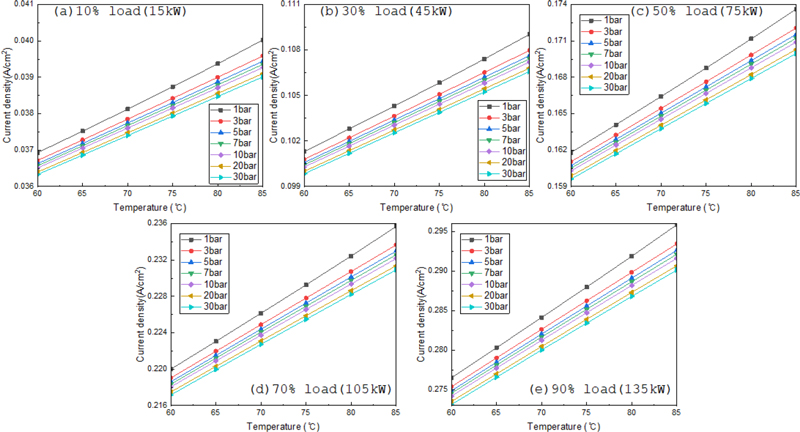
Fig. 3은 스택의 10-90% 전력 부하 조건에서 온도와 압력의 변화에 따른 전류밀도의 특성 분석 결과를 나타낸 것이다. 스택의 부하 변동은 투입되는 전력을 기준으로 하며 부하가 증가 할수록 전류 밀도가 증가한다. 10% 부하 조건에서 온도와 압력의 변화에 따라 전류 밀도는 0.03633~0.04003 A/cm²로 나타났다. 50% 부하 조건에서 전류밀도는 온도와 압력 변화에 따라 0.1595~0.1736 A/cm², 90% 부하조건에서 전류 밀도는 0.2731~0.2959 A/cm²로 나타났다. 10% 부하, 7 bar 운전조건에서 온도가 60°C에서 85°C로 증가할수록 스택의 전류밀도는 0.03657 → 0.03712 → 0.03768 → 0.03823 → 0.03880 → 0.03936 A/cm²로 증가하였으며, 85°C의 전류밀도 값은 60°C의 값보다 약 7.6% 증가하였다. 90% 부하, 7 bar 운전조건도 온도가 증가할수록 전류밀도 값이 0.2746 → 0.2781 → 0.2817 → 0.2852 → 0.2887 → 0.2921 A/cm²로 증가하며, 85°C 운전조건에서 60°C도 대비 약 6.4% 증가한 값을 보였다. 전류 밀도는 압력 대비 온도가 변화가 큰 영향을 주었다. 90% 부하 조건에서 7 bar 기준으로 60°C에서 85°C까지 온도가 증가하게 되면 셀전압은 1.957 V에서 1.840 V로 감소하게 된다. 식 (4)에 따라 전류 밀도는 투입 전력, 셀전압과 상관관계를 가지고 있으며, 동일 전력에서 셀전압이 낮아질수록 전류밀도는 증가하게 된다. 셀전압은 가역 전압에 영향을 크게 받으며 가역전압은 온도가 증가할수록 낮아지게 된다.

Fig. 3.

Results of current density by temperature and pressure based on 15 kW-135 kW

10% 부하, 70°C 운전조건에서 작동 압력이 30 bar에서 1 bar로 감소하면 0.03740 → 0.03748 → 0.03761 → 0.03768 → 0.03774 → 0.03785 → 0.03812 A/cm²로 증가하였다. 30%, 50%, 70% 부하조건에서도 70°C에서 압력이 30 bar에서 1 bar로 감소할수록 전류밀도가 각각 0.0018, 0.0026, 0.0035 A/cm²로 증가하였다. 동일한 부하와 온도조건에서 전류밀도는 압력이 감소할수록 증가하였다. 부하의 증가에 따라 전류밀도의 증가량은 증가하지만, 상대적인 증가량은 1.76 / 1.59 / 1.57%로 부하의 증가에 따라 증가량이 소폭 감소하였다. 압력이 증가할수록 기포의 크기가 작아져 저항에 의한 과전압(V_Ω)이 감소하여 스택의 효율은 증가한다. 압력 증가에 따라 활성화 과전압(V_act) 또한 감소한다. 하지만 셀 전압은 V_act값과 V_Ω값 대비 가역전압이 더 큰 영향을 미친다. 압력이 증가할 때 가역전압이 증가하게 되어 전체적인 셀 전압이 증가하게 되어전류 밀도가 감소한다.

전류밀도에 영향을 주는 인자를 파악하기 위해 해석 조건의 온도(65~80°C), 압력(1~30 bar) 에서 셀전압(V_cell)을 구성하는 요소들의 변화 추이를 확인하였다. 식 (5)에서 나타내는 셀전압의 요소 중 가역전압(E_rev)이 1.179 V에서 1.279 V의 값을 가지며 다른 값들 보다 지배적인 영향을 주었다. 활성화에 의한 전위차(V_act)가 0.5364~0.6810 V의 값을 가졌고, 저항에 의한 전위차는 0.053~0.060 V의 값을 가지며 가장 작은 값을 보였다.

식 (6)에 따라 표준가역전압는 온도에 의한 2차함수로 구성돼있고 135 kW를 기준으로 60°C, 1 bar에서 1.199 V, 85°C, 1 bar에서 1.179 V로 온도가 증가함에 따라 감소하는 것을 확인할 수 있다. 이러한 표준가역전위와 로그함수를 통해 구해지는 가역전위는 60°C, 1 bar에서 1.202 V, 85°C, 1 bar에서 1.173 V, 60°C, 30 bar에서 1.279 V, 85°C, 1 bar에서 1.263 V로 온도가 증가할 때 감소하고 압력이 증가할 때 증가하는 것을 확인할 수 있었습니다.

90% 부하 조건과 70°C의 온도 조건에서 30 bar에서 1 bar로 감소하면 셀전압은 1.919 V에서 1.891 V로 감소한다. 셀전압이 압력보다 온도에 대한 영향을 더 크다는 결과를 확인하였다. 10%~90%의 전력, 1~30 bar의 압력, 60~85°C에서 셀 전압은 1.492~1.968 V의 값을 갖는다. 70°C, 7 bar에서 전력이 10%에서 90%로 증가하면 15 kW에서 135 kW로 증가하나 셀전압은 1.585 V에서 1.908 V으로 증가한다. 셀전압이 증가하는 값 보다 더 큰 폭으로 전력이 증가하기 때문에 고전력에서 전류밀도의 값이 훨씬 더 커진다. 전류밀도 값이 증가한다.

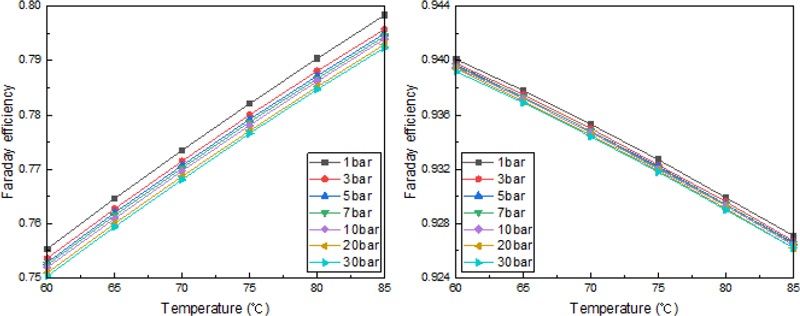
Fig. 4는 30%와 90% 부하 조건에서 온도와 압력의 변화에 따른 패러데이 효율(Faraday Efficiency (η_F))의 결과를 나타낸 것이다. 수치 해석은 10-90% 부하 조건에서 수행되었지만 대표적인 30%와 90%의 부하 조건에 대해 비교 분석을 수행하였다. 패러데이 효율은 전력 소비량의 이론적 수소 생산량 대비 실제 생산되는 수소의 비율로 계산된다. 페러데이 효율이 증가하면 수전해 스택의 효율이 비례하여 증가한다. 온도와 압력의 변화에 따른 페러데이 효율은 수전해 스택의 부하 조건에 따라 상이하게 나타난다. 10% 부하, 7 bar 운전조건에서 패러데이 효율은 온도가 60°C에서 85°C로 증가할수록 0.3003 → 0.3155 → 0.3316 → 0.3484 → 0.3364 → 0.3852로 증가하였다. 30% 부하, 7 bar 운전조건에서는 온도가 60°C에서 85°C로 증가할수록 0.7524 → 0.7615 → 0.7702 → 0.7787 → 0.7867 → 0.7954로 증가했다. 스택 온도에 따른 패러데이 효율의 변화는 10, 30, 50% 부하조건에서는 온도의 상승에 따라 패러데이 효율도 증가하였다. 또한, 부하가 10%에서 50%로 증가할수록 온도 상승에 따른 페러데이 효율 증가 폭이 감소하는 결과로 나타났다.

Fig. 4.

Results of faraday efficiency by temperature and pressure based on 45 kW, 135 kW

부하가 70%로 증가하면서 온도 증가에 따른 페러데이 효율은 감소하는 경향으로 나타났다. 70% 부하, 7 bar의 스택 조건에서는 온도가 60°C에서 85°C로 증가할수록 패러데이 효율은 0.9191 → 0.9182 → 0.9171 → 0.9159 → 0.9144 → 0.9128로 감소하였다. 90%, 7 bar에서는 0.9396 → 0.9373 → 0.9348 → 0.9321 → 0.9294 → 0.9265로 감소했다. 90%의 부하 조건이 70% 부하 조건 대비 온도에 따른 패러데이 효율 감소 폭이 증가했다.

전력 부하 10%, 70°C 조건에서 압력이 30 bar 에서 1 bar로 감소하면서 0.3284 → 0.3293 → 0.3308 → 0.3316 → 0.3324 → 0.3336 → 0.3368로 증가하며 압력의 변화에 따른 패러데이 효율의 변화폭은 0.0084로 나타났다. 30, 50, 70, 90%로 부하 조건이 증가하면서 패러데이 효율의 증가폭은 각각 0.0054, 0.0026, 0.0013, 0,0009로 감소하면서 압력의 변화에 따른 패러데이 효율의 변동 폭이 감소하였다. 부하 조건이 70%로 증가하면서 온도 증가에 따른 페러데이 효율은 감소하는 경향으로 나타났다. 동일한 온도 조건과 모든 부하 조건에서 압력이 낮아 질수록 페러데이 효율을 증가했다. 하지만, 높은 부하에서 증가폭은 감소하는 경향으로 나타났다. 압력의 변화에 따른 페러데이 효율 변화는 PEM 수전해에서도 동일한 경향을 나타낸다.^[25] 패러데이 효율은 온도와 전류에 영향을 받는다. 70%, 90% 부하일 때 1 bar 조건에서 온도의 증가에 따라 패러데이 효율의 값이 각각 0.9199에서 0.9138, 0.9401에서 0.9271로 감소하였다. 패러데이 효율은 수소 생산량과 상관관계를 가진다.

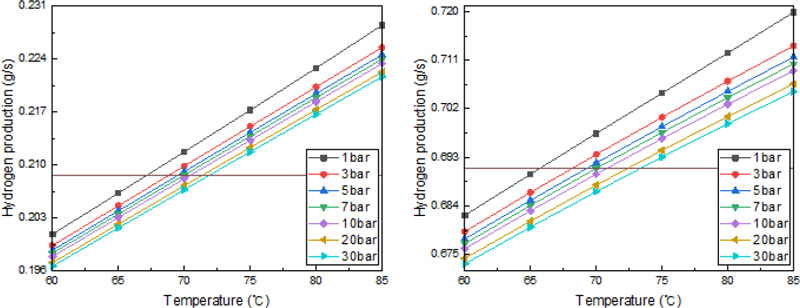
Fig. 5는 30%와 90%의 부하 조건에서 온도와 압력의 변화에 따른 수소 생산량에 대해 나타낸 것이다, 그래프의 가로 실선은 알카라인 수전해 시스템의 일반적인 운전 조건인 70°C와 7 bar에서 생산되는 수소량을 의미한다. 30% 부하 조건, 7 bar 조건에서 온도가 60°C에서 85°C까지 증가하면서 수소 생산량은 0.1983 → 0.2035 → 0.2086 → 0.2138 → 0.2189 → 0.2240 g/s로 증가했다. 90% 부하, 7 bar 조건에서는 온도의 상승에 따라 수소 생산량이 0.6770 → 0.6841 → 0.6910 → 0.6976 → 0.7041 → 0.7103 g/s로 증가했다. 동일한 부하 조건에서 온도와 압력에 따라 수소 생산량은 전류밀도의 결과와 동일한 경향으로 나타났다. 모든 부하조건에서 온도 증가와 압력 감소에 따라 수소 생산량은 증가하는 경향으로 나타났다.

Fig. 5.

Results of hydrogen production by temperature and pressure based on 45 kW, 135 kW

70%와 90% 부하 조건에서 패러데이 효율은 온도 상승에 따라 감소하였지만 패러데이 효율을 고려한 수소 생산량은 온도의 상승에 따라 증가했다. 70% 부하, 7 bar 조건에서 온도의 상승에 따라 패러데이 효율의 변화량은 60°C 기준 0.69% 감소였다. 하지만, 전류밀도의 변화량은 60°C 기준 6.5% 증가하였다. 90% 부하, 7 bar 조건에서는 60°C 전류밀도는 6.33% 증가했으며 패러데이 효율은 1.39% 감소했다. 수소 생산량은 패러데이 효율과 전류 밀도를 통해 계산된다. 70%, 90% 부하조건에서 수소 생산량은 전류 밀도의 변화량이 더 크기 때문에 전류밀도의 경향성과 동일하게 모든 부하조건에서 온도의 상승에 따라 증가했다. 30% 부하와 70°C 온도 조건에서 압력이 1 bar에서 30 bar까지 증가하면서 수소 생산량은 0.2117 → 0.2099 → 0.2086 → 0.2082 → 0.2072 → 0.2067 g/s로 감소했다. 90% 부하와 70°C 온도 조건에서 압력 증가에 따라서 수소 생산량은 0.6974 → 0.6935 → 0.6920 → 0.6910 → 0.6899 → 0.6879 → 0.6867 g/s로 감소했다. 패러데이 효율은 모든 전력 부하조건에서 압력 상승에 따라 감소했으며 수소 생산량도 압력의 상승에 따라 감소하였다.

3.2 부하, 온도, 압력에 따른 BOP 운전 특성 분석 결과

Table 4는 각 온도와 압력 조건에서 BOP 시스템의 열교환기, 냉각기와 응축기의 열전달을 종합하여 나타낸 것이다. BOP 시스템의 스택 해석은 수치해석 결과(수소, 산소, 전해질, 물의 출구 온도, 조성 등)를 연계하여 수행되었다. 본 연구에서 기준 운전 조건은 7 bar, 70°C이다. 3.1에서 설명한 바와 같이 기준 조건의 수소 생산량을 기준으로 각 부하별 압력 조건에 따른 온도 변화를 산정하였다. 기준조건과 동일한 수소 생산량 조건과 동일한 부하 조건에서 압력이 증가할수록 스택의 출구 온도는 높아지게 된다. 따라서, 압력이 증가할수록 스택 작동 온도를 맞추기 위해 열교환기의 냉각 열량이 증가하게된다. 스택의 운전 부하가 증가할수록 스택 출구에서 배출되는 물질의 온도가 증가하게 되어 BOP 총 열전달량은 증가하게 된다. 열교환기, 냉각기, 응축기 중 열전달량은 열교환기가 약 96~99%의 비율을 차지하며 냉각기와 응축기의 비율은 약 1~4%로 나타난다. 스택에서 배출되는 물과 전해질, 수소, 산소는 열교환기로 투입하게 되어 스택 입구 온도로 냉각된 후 기수분리기로 투입하게 된다. 기수분리기에서 물과 전해질은 재순환하게 되며 각각의 수소와 산소 가스만 냉각기와 응축기를 통과하게 된다. 스택에서 배출되는 물질 중 가스인 수소와 산소의 비율은 전해질과 물에 비해 매우 작다. 따라서, 열교환기의 열전달량이 냉각기와 응축기 대비 높게 나타난다.

Table 4.

Results of total heat transfer of BOP system

BOP 시스템 전력 소모량은 열교환기, 냉각기와 응축기의 냉각을 히트펌프를 통한 방식으로 고려하였으며 열전달량/3(COP)로 계산했다. 스택으로 물과 전해질의 투입은 펌프를 통해 이루어지며 각 부하별 스택의 압력 강하 5%를 고려하여 펌프의 전력소모량을 계산했다.^[26]

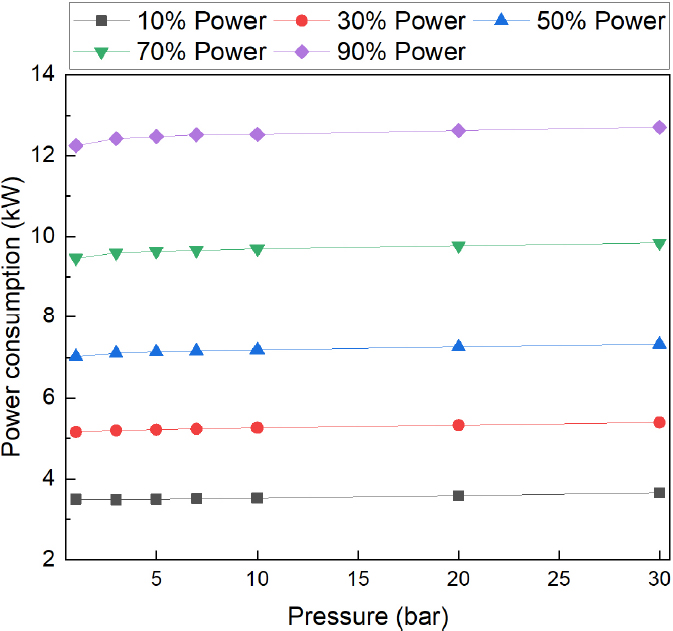
총 전력 소모량은 히트펌프의 전력 소모량과 펌프 전력소모량을 합하여 Fig. 6과 같이 나타내었다. BOP 시스템의 전력 소모량은 압력과 부하가 증가 할수록 열전달과 동일한 경향으로 증가했다. 10%의 부하조건의 스택의 전력은 15 kW이며 BOP의 전력소모량은 약 3.5 kW로써 스택의 전력소모량 대비 BOP의 전력소모량은 약 23%에 해당한다. 스택의 부하가 증가할수록 스택의 전력소모량 대비 BOP의 전력소모량은 50%(75 kW) 부하 조건에서 9.5%이며 90%(135 kW) 부하 조건에서 9.2%로 낮아졌다. BOP 시스템의 기수분리기에서 물/전해질과 수소/산소는 분리되며 수소/산소가 생성된 질량만큼 새로운 물이 공급되어 스택으로 투입되는 물과 전해질의 농도는 모든 조건이 동일하다. 낮은 부하에서 BOP의 전력소모량이 스택의 전력소모량 대비 높으며 전체 수전해 시스템의 효율도 낮게 나타난다.

Fig. 6.

Power consumption of BOP system

펌프의 전력 소모량은 0.05-0.15 kW로 히트펌프의 전력소모량 3.4-12.7 kW 대비 매우 낮게 나타났다. BOP 시스템의 공정 해석은 정상 상태 기준으로 수행되었다. 따라서 펌프의 전력소모량은 물과 전해질의 유량 투입과 스택의 압력강화를 보상하는 전력만 요구되기 때문에 낮게 나타난다. 알카라인 수전해 시스템의 Start-up 조건과 작동 압력이 변화하는 조건에서는 펌프의 전력소모량은 증가하게 된다.

3.3 압력과 온도 제어를 통한 스택의 운영 최적화 방안 평가

Table 5는 온도와 압력 변화에 따라 수소 생산량에 대해 본 연구의 기준 스택 운영 조건은 7 bar, 70°C를 기준으로 정리한 내용이다. 수소 생산량은 압력이 낮아질수록, 온도가 증가할수록 증가하였다. 그 결과 모든 부하조건에서 30 bar, 60°C 조건에서 가장 낮은 수소 생산량을 보였으며, 1 bar, 85°C 조건에서의 가장 높은 수소 생산량을 보였다. Fig. 5에서 나타낸 것처럼 온도 및 압력의 범위 이내의 다양한 수소생산량을 계산하였지만, Table 5는 기준 스택 운영 조건인 7 bar 70°C와 최대, 최소값만 정리하였다. 본 연구에서는 부하 변동 대응을 위해 기준 조건인 7 bar, 70°C의 조건에서 1차로 압력을 제어하고 2차로 온도를 제어하여 수소 생산량 변화에 대한 Table 5와 같이 영향 분석을 수행하였다. 부하 10% 조건에서 1 bar로 압력을 줄이면 0.0009 g/s의 수소 생산량이 증가했으며 30 bar로 압력을 증가하면 0.00056 g/s의 수소 생산량이 감소하였다. 부하 10% 조건에서 압력 변화 시 기준 조건의 수소 생산량 대비 약 1.7-2.7%의 수소 생산량이 변화한다. 1 bar로 압력을 저감시킨 후 온도를 85°C로 증가할 경우 수소 생산량은 0.00849 g/s으로 기준 조건 대비 25.8% 증가하였으며, 압력을 30 bar 로 증가한 후 온도를 60°C로 낮추면 수소 생산량은 0.0042 g/s가 기준조건 대비 13.34% 감소했다. 90%의 부하 조건에서는 1bar와 30 bar로 압력 변화에 따라 각각 +0.0064 g/s, -0.0043 g/s로 변화하게 된다. 1차 압력을 제어 후 85°C와 60°C로 스택의 운전 온도를 제어하면 각각 +0.0289 g/s와 -0.0178 g/s 만큼 기준 조건 대비 최대 + 4.18%, -2.5%로 수소 생산량이 변화하게 된다.

Table 5.

Evaluation of the effect of temperature and pressure on hydrogen production in a stack

저부하 운전 조건에서는 압력과 온도 변화에 따라 수소 생산량의 영향이 크지만 부하가 증가하면서 압력과 온도에 따른 수소 생산량의 변화는 감소하게 된다.

4. 결 론

본 연구에서는 알카라인 수전해 시스템의 부하 변동 대응을 위해 온도와 압력을 동시에 변화하는 조건에서 스택과 BOP의 운전 특성 평가를 수행하였다. 알카라인 수전해 시스템의 운전 제어는 변동성이 빠른 압력을 1차 제어하고 변동성이 비교적 느린 온도를 2차로 제어하기 위한 목적으로 연구를 수행하였다.

알카라인 수전해 시스템의 스택과 BOP 해석은 각각 수치해석과 공정해석을 통해 온도와 압력 변화에 따른 수소 생산 특성에 대해 전류 밀도, 패러데이 효율, 수소생산량, 전력소비량을 비교하였다. 동일한 부하조건에서 스택은 압력이 낮아질수록 수소 생산량(스택 효율)은 증가하게 되고 작동 온도가 증가할수록 수소 생산량은 증가하게 된다. 스택의 수소 생산량은 압력 제어 대비 온도제어의 영향이 크다. BOP 시스템은 낮은 부하에서 스택에 투입되는 전력 대비 BOP의 전력 소모량이 크며 부하가 증가할수록 BOP의 전력 소모량은 작아지게 된다.

본 연구의 기준 운전 조건인 7 bar 대비 낮은 압력 조건에서 수소 생산량은 증가하고 전력 소비량은 낮아지지만 압력의 감소로 인해 수소의 순도(Purity)가 감소하게 된다. 또한, 작동 압력이 낮아질수록 설비의 규모가 증가하고 생산된 수소의 이송 및 저장하는 측면에서 단점이 발생한다. 또한, 스택 운전 과정에서 압력 변화 시 기수 분리기의 제어(수위 조절, 추가 물 추가 등)가 요구된다. 스택에 투입되는 물과 전해질의 유량이 동일한 조건에서 온도 제어는 반응이 느리지만 온도 제어를 위해 물과 전해질의 유량을 변경할 경우 온도 제어를 통해 부하 변동을 효과적으로 대응할 수 있다.

본 연구를 통해 도출된 부하 조건 별 온도와 압력에 따른 알카라인 수전해의 스택 및 BOP의 운전 특성 분석 결과를 기반으로 향후 부하 변동 조건 혹은 스택의 가동 조건과 같이 부하가 변하는 동적 모델의 기초자료로 활용이 가능하다. 부하 변동 조건에서 온도 및 압력의 조절을 통해 수소생산량 및 에너지 사용량의 변화를 최소화 할 수 있는 시스템의 설계 및 운영의 기초 자료로 확장할 수 있다.

Acknowledgments

본 연구는 산업통상자원부의 재원으로 한국산업기술기획평가원(KEIT)의 소재부품기술개발사업으로 수행된 연구임(20022462).

References

• Campen, A., Mondal, K., and Wiltowski, T., 2008, “Separation of hydrogen from syngas using a regenerative system”, Int. J. Hydrogen Energy, 33(1), 332-339. [https://doi.org/10.1016/j.ijhydene.2007.07.016]
• Armaroli, N., and Balzani, V., 2011, “The hydrogen issue”, ChemSusChem, 4(1), 21-36. [https://doi.org/10.1002/cssc.201000182]
• Cao, S., and Alanne, K., 2015, “Technical feasibility of a hybrid on-site H2 and renewable energy system for a zero-energy building with a H2 vehicle”, Appl. Ener gy, 158, 568-583. [https://doi.org/10.1016/j.apenergy.2015.08.009]
• Koo, B., and Jung, S.P., 2022, “Trends and perspectives of microbial electrolysis cell technology for ultimate green hydrogen production”, J. Korean Soc. Environ. Eng., 44(10), 383-396. [https://doi.org/10.4491/KSEE.2022.44.10.383]
• Molnarne, M. and Schroeder, V., 2019, “Hazardous properties of hydrogen and hydrogen containing fuel gases”, Process Saf. Environ. Prot., 130, 1-5. [https://doi.org/10.1016/j.psep.2019.07.012]
• Hadjipaschalis, I., Poullikkas, A., and Efthimiou, V., 2009, “Overview of current and future energy storage technologies for electric power applications”, Renew. Sustain. Energy Rev., 13(6-7), 1513-1522. [https://doi.org/10.1016/j.rser.2008.09.028]
• Wang, S., Lu, A., and Zhong, C.J., 2021, “Hydrogen production from water electrolysis: role of catalysts”, Nano Convergence, 8, 4. [https://doi.org/10.1186/s40580-021-00254-x]
• Sapountzi, F.M., Gracia, J.M., Weststrate, C.J., Fredriksson, H.O.A., and Niemantsverdriet, J.W., 2017, “Electrocatalysts for the generation of hydrogen, oxygen and synthesis gas”, Progress in Energy and Combustion Science, 58, 1-35. [https://doi.org/10.1016/j.pecs.2016.09.001]
• Siracusano, S., Baglio, V., Briguglio, N., Brunaccini, G., Di Blasi, A., Stassi, A., Ornelas, R., Trifoni, E., Antonucci, V., and Aricò, A.S., 2012, “An electrochemical study of a PEM stack for water electrolysis”, Int. J. Hydrogen Energy, 37(2), 1939-1946. [https://doi.org/10.1016/j.ijhydene.2011.06.019]
• Chi, J., and Yu, H., 2018, “Water electrolysis based on renwable energy for hydrogen production”, Chineses Jornal of Catalysis, 39(3), 390-294. [https://doi.org/10.1016/S1872-2067(17)62949-8]
• Nechache, A., and Hody, S., 2019, “Test and evaluation of an hybrid storage solution for buildings, based on a reversible high-temperature electrolyzer”, ECS Trans., 91(1), 2485. [https://doi.org/10.1149/09101.2485ecst]
• Marini, S., P. Salvi, P. Nelli, R. Pesenti, M. Villa, M. Berrettoni, G. Zangari and Y. Kiros, 2012, “Advanced alkaline water electrolysis”, Electrochim. Acta, 82, 384-391. [https://doi.org/10.1016/j.electacta.2012.05.011]
• Jang, D., Choi, W., Cho, H.S., Cho, W.C., Kim, C.H., and Kang, S., 2021, “Numerical modeling and analysis of the temperature effect on the performance of an alkaline water electrolysis system”, J. Power Sources., 506, 230106. [https://doi.org/10.1016/j.jpowsour.2021.230106]
• Jang, D., Cho, H.S., and Kang, S., 2021, “Numerical modeling and analysis of the effect of pressure on the performance of an alkaline water electrolysis system”, Appl. Energy, 287, 116554. [https://doi.org/10.1016/j.apenergy.2021.116554]
• Sánchez, M., Amores, E., Abad, D., Rodríguez, L., and Clemente-Jul, C., 2020, “Aspen Plus model of an alkaline electrolysis system for hydrogen production”, Int. J. Hydrogen Energy, 45(7), 3916-3929. [https://doi.org/10.1016/j.ijhydene.2019.12.027]
• Brauns, J., and Turek, T., 2020, “Alkaline water electrolysis powered by renewable energy: A review”, Processes, 8(2), 248. [https://doi.org/10.3390/pr8020248]
• Hu, S., Guo, B., Ding, S., Yang, F., Dang, J., Liu, B., Gu, J., Ma, J., and Ouyang, M., 2022, “A comprehensive review of alkaline water electrolysis mathematical modeling”, Appl. Energy, 327, 120099. [https://doi.org/10.1016/j.apenergy.2022.120099]
• Ursúa, A., Marroyo, L., Gubía, E., Gandía, L.M., Diéguez, P.M., and Sanchis, P., 2009, “Influence of the power supply on the energy efficiency of an alkaline water electrolyser”, Int. J. Hydrogen Energy, 34(8), 3221-3233. [https://doi.org/10.1016/j.ijhydene.2009.02.017]
• LeRoy, R.L., Bowen, C.T., and LeRoy, D.J., 1980, “The thermodynamics of aqueous water electrolysis”, J. Electrochem. Soc., 127(9), 1954. [https://doi.org/10.1149/1.2130044]
• Hammoudi, M., Henao, C., Agbossou, K., Dubé, Y., and Doumbia, M.L., 2012, “New multi-physics approach for modelling and design of alkaline electrolyzers”, Int. J. Hydrogen Energy, 37(19), 13895-13913. [https://doi.org/10.1016/j.ijhydene.2012.07.015]
• Diaz, H., and Camilo, C., 2011, “Modélisation multi-physique et électrique d'un électrolyseur alcalin”, Université du Québec à Trois-Rivières, 123.
• Manabe, A., Kashiwase, M., Hashimoto, T., Hayashida, T., Kato, A., Hirao, K., Shimomura, I., and Nagashima, I., 2013, “Basic study of alkaline water electrolysis”, Electrochim. Acta, 100, 249-256. [https://doi.org/10.1016/j.electacta.2012.12.105]
• Sánchez, M., Amores, E., Rodríguez, L., and Clemente-Jul, C., 2018, “Semi-empirical model and experimental validation for the performance evaluation of a 15 kW alkaline water electrolyzer”, Int. J. Hydrogen Energy, 43(45), 20332-20345. [https://doi.org/10.1016/j.ijhydene.2018.09.029]
• Bi, X., Wang, G., Cui, D., Qu, X., Shi, S., Yu, D., Cheng, M., and Ji, Y., 2025, “Simulation study on the effect of temperature on hydrogen production performance of alkaline electrolytic water”, Fuel, 380, 133209. [https://doi.org/10.1016/j.fuel.2024.133209]
• Tijani, A.S., and Rahim, A.H.A., 2016, “Numerical modeling the effect of operating variables on faraday efficiency in PEM electrolyzer”, Procedia Technology, 26, 419-427. [https://doi.org/10.1016/j.protcy.2016.08.054]
• Qi, R., Becker, M., Brauns, J., Turek, T., Lin, J., and Song, Y., 2023, “Channel design optimization of alkaline electrolysis stacks considering the trade-off between current efficiency and pressure drop”, J. Power Sources, 579, 233222. [https://doi.org/10.1016/j.jpowsour.2023.233222]