1 GW급 부유식 해상풍력발전단지의 배치 최적화에 관한 연구
© 2025 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study provides a foundation for the conceptual design and performance analysis of a large-scale centralized offshore green hydrogen production and storage platform. It focuses on optimizing the layout of a 1 GW-class floating offshore wind farm to maximize power generation while minimizing costs. To achieve this objective, a site near the Donghae gas plant in the East Sea was selected as a candidate location for the floating offshore wind farm. Wind resource analysis was conducted using MERRA-2 reanalysis data provided by NASA. The Jensen wake model was applied, and an optimization objective function was developed that considered both the wind occurrence frequencies by direction and in-field cable costs of the farm. Continuous Ant Colony Optimization was performed. Consequently, the power generation estimates were calculated by statistically considering the actual wind occurrence frequencies at the farm sites, ensuring realistic power production results.
Keywords:
Layout optimization, Floating offshore wind farm, Continuous ant colony optimization, Donghae gas field키워드:
배치 최적화, 부유식 해상풍력발전단지, 연속적 개미 군집 최적화, 동해 가스전1. 서 론
최근 네덜란드(PosHYdon,[1] H2opZee[2])와 독일(H2Mare[3])에서 부유식 해상풍력발전단지와 수소 생산시설을 통합하는 파일럿 프로젝트가 진행 중이다. 국내에서도 울산 부유식 해상풍력단지를 기반으로 해양그린수소 생산 프로젝트가 계획되고 있다. 부유식 해상풍력단지의 여유 전력을 이용한 수소 생산은 재생가능 에너지를 이용하는 그린수소 기술로 분류되어 화석연료 기반의 수소보다 친환경적이다. 그리고 풍력발전 여유 전력을 활용하므로 수소 생산 단가를 낮출 수 있으며, 대규모의 해상풍력단지와 수소 생산시설의 통합 운영은 장기적으로 해상풍력의 경제적 경쟁력을 높일 수 있는 장점이 있다. 본 논문은 대용량 집중형 해양그린수소의 생산・저장 플랫폼 개념설계 및 성능해석 기술개발을 위해 수행된 부유식 해상풍력발전단지의 풍력터빈 배치 최적화를 위한 기초 연구이다.
기존 연구들은 부유식 해상풍력단지의 효율적인 배치와 설계에 대한 다양한 접근법과 분석에 관한 연구를 제안하고 있다. 예를 들어, 유전 알고리즘을 활용한 연구에서는 선박자동식별장치(AIS) 데이터를 기반으로 계절별 풍력단지의 최적 위치를 선정하여 에너지 생산을 최적화한 바 있다.[4] 또한, 전산유체역학 해석을 통해 풍력터빈 간의 후류 영향을 분석하고 연간 에너지 생산량을 극대화하는 방법론이 제시되었다.[5] 풍속, 풍력 발전량, 그리고 풍속에 영향을 미치는 환경적 요인을 측정하여 데이터 세트를 구성하여 머신러닝과 데이터 마이닝을 적용한 풍력발전 예측 시스템에 대한 연구도 수행되었다.[6] 그리고 기상 조건에 따른 바람과 파랑의 불일치로 인한 요(Yaw) 오차가 15 MW급 부유식 해상풍력터빈의 출력 성능과 구조적 안정성 향상을 위한 연구도 수행된 바 있다.[7] 이러한 연구들은 단순히 터빈을 배치하는 데 그치지 않고, 발전기의 특성을 고려하여 실질적인 설계와 운영에 대한 통찰을 제공한다.
부유식 해상풍력터빈의 동적 특성을 고려한 후류 분석도 중요한 연구 주제이다. 비정상 와류 격자 기법을 활용한 연구는 풍력단지 내 발전기의 위치를 최적화하여 후류 간섭을 최소화하는 방안을 도출하였다.[8] 나아가, 부유식 풍력발전과 파력발전을 연계한 복합 발전 시스템에서 다수의 풍력터빈 배치를 설계하고 성능을 평가하는 연구도 진행되고 있다.[9] 이러한 접근법은 단지의 설계 초기 단계에서부터 종합적인 시스템 최적화를 가능하게 한다.
이처럼 부유식 해상풍력발전단지의 배치 최적화는 기술적 혁신과 새로운 설계 방안을 도출하는 핵심 요소로 주목받고 있다. 본 연구는 부유식 해상풍력발전단지의 배치 최적화 과정에서 기존의 접근법과 차별화를 두고 있다. 기존 연구들이 주로 바람 자원 분석과 후류 설계를 중심으로 배치 최적화를 수행한 데 반해, 본 연구는 이러한 요소들에 더해 OWF 설치 비용을 더욱 세부적으로 분석하여 최적화에 반영하였다. 특히, 내부 케이블 설치 비용을 중요한 기저변수로 추가하고 이를 배치 최적화 알고리즘의 최적화 목적함수에 포함함으로써, 설치 비용 절감과 발전 효율성을 동시에 개선할 수 있는 구체적이고 실질적인 설계 방안을 모색하였다.
2. 부유식 해상풍력발전단지 모델링
2.1 해역 선정 및 바람 자원 데이터 획득
부유식 해상풍력발전단지 조성 대상 해역은 울산에서 남동쪽으로 약 58 km 떨어져 있는 동해가스전 인근 해역이다. 이 해역은 풍부한 바람 자원을 바탕으로 부유식 해상풍력 발전단지가 국내 최초로 조성될 해역이다.[10]
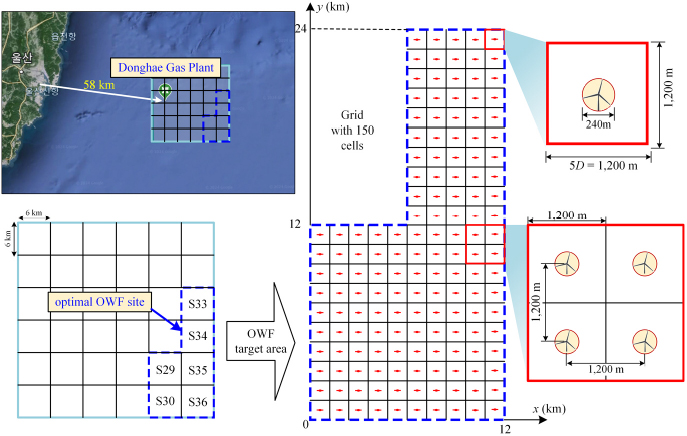
본 연구에서 활용하기 위한 OWF 대상 해역을 선정하기 위해, 유전 알고리즘을 활용하여 부유식 OWF의 최적 위치를 제안한 연구를 활용하였다.[4] 이 연구는 Fig. 1과 같이 동해 가스전 인근 해역을 6 km × 6 km의 36개의 구역으로 나누어, 선박의 밀집도와 운항 패턴을 토대로 최적의 부유식 OWF 위치 선정을 수행하였다. 최적 위치로 선정한 11개의 구역 중, 본 연구에서는 6개 구역(S29, S30, S33-S36 Fig. 1 참조)을 부유식 OWF 대상 해역으로 선정하였다.
본 연구에서 선정한 OWF 영역에 대해, 부유식 WT의 계류 반경을 고려하지 않고 임의로 2가지 WT 배열 간격을 설정하였다. 즉, 최소 WT 간격으로 설정한 5D(=1,200 m) [9,11~13] 와 주어진 OWF 영역 내에서 67기의 WT를 최대 간격으로 배치할 수 있는 간격 7D(=1,680 m)를 고려하였다. 대상 해역을 5D 간격으로 배치할 경우, 1,200 m × 1,200 m 크기의 150개의 격자로 구성할 수 있으며(Fig. 1 참조), 각 격자의 중심에 WT를 설치한다고 설정하였다.
OWF 대상 해역의 바람 자원 데이터 획득을 위해 NASA의 고다드 지구과학 데이터 및 정보 서비스 센터(GES DISC)에서 제공하는 MERRA-2 재해석 데이터를 활용한다. MERRA-2 재해석 자료는 전 지구를 약 0.5°×0.625° 격자로 설정하고 각 격자에서의 재해석 기상 자료를 제공한다.[15]
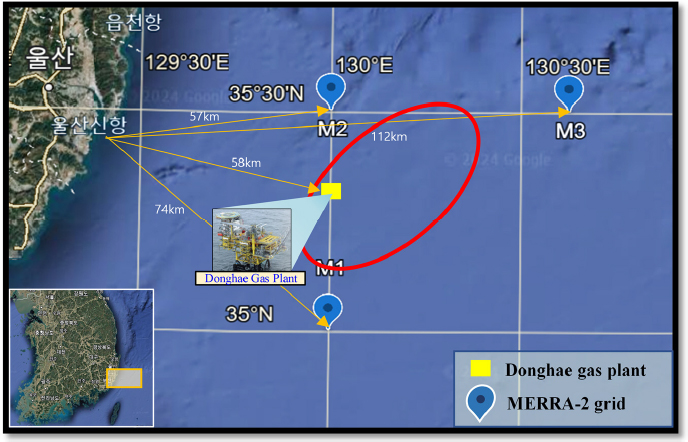
본 연구에서는 Fig. 2와 같이, 가스전 인근 위치한 3개의 MERRA-2 격자점 위치(M1~M3)에서 제공하는 재해석 바람 자료를 평균하여 바람 설계에 활용하였다. 재해석 자료는 각 격자점 위치에서 2014년 1월 1일 0시부터 2023년 12월 31일 23시까지의 10년 간의 해수면 위 10 m와 50 m 높이에서의 동서바람(Eastward Wind)과 남북바람(Northward Wind) 성분을 합성하여 1시간 평균 풍속과 풍향 성분 데이터(각각 87,216개의 재해석 데이터)를 포함한다. 풍향은 북쪽을 0°로 동쪽을 90°로 정의하고, 공기 밀도는 국제전기기술위원회(IEC)[16]에서 정한 표준에 따라 1.225 kg/m3로 설정하였다.
해상풍력터빈의 전력 생산량을 계산하기 위해서는 허브 높이에서의 풍속과 풍향 데이터가 필요하다. 본 연구에서는 대상 해역이 육지에서 60 km 이상 떨어진 공해상에 있어 장애물에 의한 바람의 교란됨이 적어 풍속과 풍향이 대상 해역 전체에서 균일하다고 가정한다. 그리고 풍향은 수직 방향으로 동일하다고 가정하여 기준고도(10 m)에서의 재해석 데이터를 기준으로 설정하였다. 풍속은 기준 고도 풍속을 해상풍력터빈의 설계 요구 사항을 정의하는 국제 표준인 IEC61400-3-1(3.76)에 소개된 멱법칙(Power Law)을 활용하였다.[16]
| (1) |
멱법칙 지수는 해상에서 0.1~0.2로 통상적으로 사용되며,[17] IEC 61400-3-1의 표준에서는 약 0.14로 추천하고,[16] Heu et al.(1994)은 바다에서 사용할 수 있는 최적의 추정값으로 0.11을 제안하였다.[18] 본 연구에서는 멱법칙 지수를 0.11로 설정하였다.
풍황 모델링을 위해 풍향을 16방위로, 풍속 구간을 0.5 m/s로 분류하였다. 이 결과를 바탕으로, 풍향별 바람의 발생 빈도를 3-매개변수 Weibull 분포를 이용하여 나타낼 수 있다.
| (2) |
Table 1은 3-매개변수 Weibull 분포의 풍향별 매개변수, 발생 빈도와 평균 풍속을 나타낸다.[19] Table 1을 통해, 이 해역은 발생 빈도를 기준으로 주풍향은 북동쪽이며, 부풍향은 북서쪽이다.
Table 1에서 풍향별 평균 풍속은 Weibull 확률분포를 이용하여 식 (3)과 같이 구한다.
| (3) |
2.2 해상풍력발전기 선정
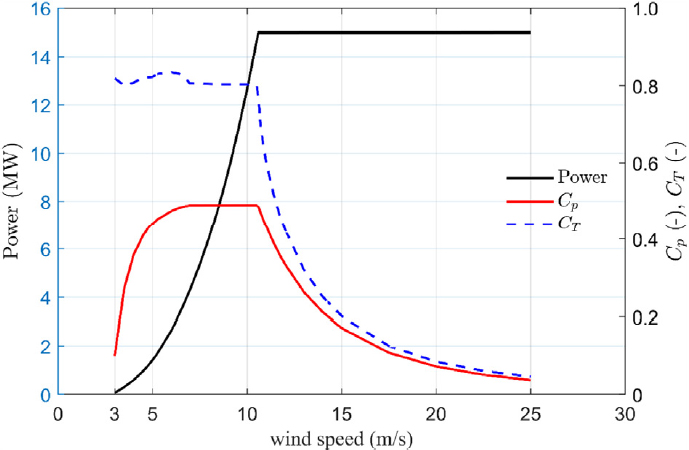
본 연구에서는 대용량 부유식 해상풍력발전기로 구성된 1 GW급 OWF의 구성을 위해 상세한 터빈의 제원이 공개된 참조모델을 선정하였다. 이에 따라 미국 재생에너지연구소(이하 NREL)에서 제공하는 15 MW급 참조 풍력터빈(RWT)을 선정하였다.[20] 본 연구에서는 터빈이 바람의 방향을 따라 회전하는 요잉(yawing) 시스템을 가정하였다. Table 2는 참조 터빈의 제원을 나타내며, Fig. 3은 RWT의 풍속에 따른 출력 곡선 P, 출력 계수 곡선 Cp와 추력 계수 곡선 CT를 나타낸다.
2.3 Jensen 후류 모델
본 연구에서는 후류 모델 중 간단하고 빠른 계산이 필요한 초기 설계 단계에 적합한 Jensen 모델에 기반한 Park 1 후류 모델을 활용하였다.[21~26] 바람의 흐름이 상류에 설치된 풍력터빈 날개의 회전으로 인해 회전자 뒤쪽에 풍속의 저하, 즉 후류로 인하여 하류에 있는 풍력터빈으로의 유입 풍속이 저하되어 발전 성능이 저하된다. 따라서 OWF의 성능을 극대화하기 위해서는 후류 설계가 중요하다.
OWF의 대상 해역 내에 총 Nwt개의 터빈이 위치하며, 각각의 위치를 직교좌표계 상에서 X=[x1,⋯, xNwt], Y=[y1,⋯, yNwt]로 나타낸다. 풍향을 기준으로 하류에 있는 WT i의 좌표를 (xi,yi), 상류의 WT j의 좌표를 (xj,yj)로 설정한다. 직교좌표계의 x-축을 반시계 방향으로 θ(=3π/2-θd) 만큼 회전하여 x-축의 양의 방향을 풍향과 평행하게 설정한다. x’-좌표계 상에서 WT의 좌표를 이용하여 후류 설계의 편의성을 증대할 수 있다.[23]
| (4) |
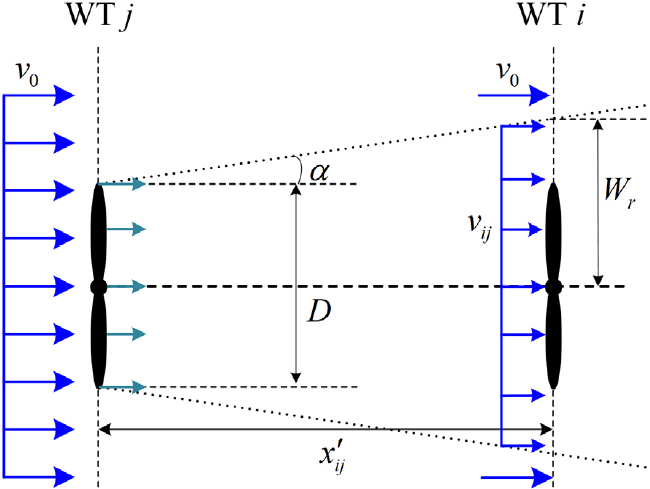
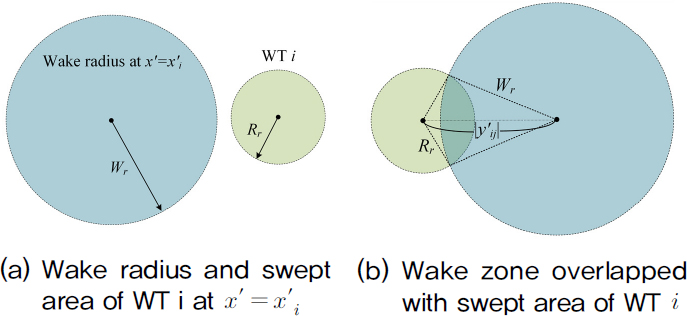
이 좌표계에서 상류와 하류의 WT의 종방향 거리는 x’ij(=x’i-x’j>0), 횡방향 거리는 |y’ij|(=|y’i-y’j|)이다. Fig. 4와 같이, 상류의 WT로 유입되는 풍속 vd와 하류의 WT i(x’=x’i)로 유입되는 저하된 풍속 vij의 비 vij/vd는 식 (5)와 같다.
| (5) |
여기서, Rr은 로터 반지름이며, 후류 감쇄 계수(혹은 후류 확장비) α를 구하기 위해, 표면 거칠기 길이 z0를 공해상에서 쓰이는 0.0002 m로 설정하였다.[27,28] 또한 상류에서 발생한 후류 반경과 하류에 있는 WT i의 회전 면적의 겹침 면적(Fig. 5 참조)은 식 (6)과 같다.
| (6) |
이제 OWF내 배치된 다수의 WT과 풍향에 따라 발생한 후류 영역을 동시에 고려한 임의의 WT i로 유입되는 풍속은 식 (7)과 같다.
| (7) |
2.4 OWF 비용 분석 및 최적화 목적함수
WT 배치에 따른 OWF의 전력 생산량을 계산하기 위해, Fig. 3의 WT의 출력 곡선과 Table 1의 풍향별 3-변수 Weibull 분포를 활용한다. 실제적인 전력 생산량을 계산하기 위해, 후류, 풍향과 풍향별 바람 발생 빈도수(%)를 고려한다. 식 (8)은 풍향별(θd, d=1,...,16) 전력 생산량, 식 (9)는 바람 발생 빈도수를 고려한 평균 전력 생산량(MWh)을 나타낸다.
| (8) |
| (9) |
한편, 2021년도 부유식 OWF의 비용(CapEx)을 구성하는 요소는 WT 자체 비용이 23.3%, 부대 설치 비용(Balance of System)을 구성하는 하부 구조 및 기초 비용이 37.5%, 전기 인프라 비용이 13.4%, 조립 및 설치 비용이 5.7%, 그 외 간접 비용 등이 20.1%를 차지한다.[29] 고정식 WT의 경우, 터빈 자체 비용이 전체 비용의 33.6%를 차지하고 하부 구조 및 기초 비용이 17.9%를 차지한다. 따라서 고정식 OWF에 비해 부유식 OWF의 비용에서 하부 구조 및 기초 비용이 중요하게 고려되어야 한다.
이에 따라 OWF의 최소 비용-최대 전력 생산을 위한 최적화 목적함수 중, 비용의 변수는 터빈 자체의 비용, 하부 구조 및 기초 비용, 전기 인프라 비용, 조립 및 설치, 그 외 간접 비용 등이 종합적으로 고려되어야 한다. 하지만 이러한 모든 변수를 동시에 고려할 경우, 배치 최적화 과정에서 알고리즘의 효율이 저하될 수 있다. 이에 따라, 최적화의 효율을 높이기 위해, 비용을 구성하는 요소들을 살펴보고 최적 배치 최적화 목적함수를 구성하는 변수를 최소화한다.
본 연구에서는 최적의 WT 배치와 상관없이 일정한 값을 가지는 변수는 최적화 목적함수에 고려하지 않았다. 예를 들어, WT 자체의 비용, 하부 구조물 및 기초 비용, 조립 및 설치의 경우, 최적 배치와 상관없이 같은 비용이므로 최적화 변수에서 제외하였다. 그리고 전기 기반 비용은 OWF 내의 전력 송배전망 연결을 위한 인프라 구축 비용, 케이블 설치 비용 등을 포함한다. 이때, 전기 인프라 구축 비용은 OWF 내 케이블과 육지 송전 케이블의 비용과 길이, 굽힘 보강기(Bend Stiffener) 및 연결장치(Connector)로 구성된다. 그리고 케이블 설치 비용은 케이블의 길이, 설치 선박의 일별 설치 길이와 그에 따른 운임 등의 함수이다.[30]
따라서 전기 기반 비용들은 공통으로 케이블 길이의 함수이고, 케이블 길이는 WT의 최적 배치 결과에 의존하므로 최소 연결 길이를 통해 비용을 최소화할 수 있다. 본 연구에서는 최적화 배치 결과를 도출하기 위해 실제 부유식 해상풍력터빈의 계류를 구성하는 동적 케이블(Dynamic Cable)의 길이와 케이블 내부의 전기적 손실률도 고려하지 않는다. 이에 따라, 본 연구에서는 OWF 내부의 WT 간 직선거리만을 고려한 최소 길이 연결 비용 대비 최대 전력 생산량을 최적화 목적함수로 설정하였다.
| (10) |
여기서, 케이블 부설선의 임차비는 90 백만원/일(1€ = 1,500 원 적용), 케이블 1 km당 설치 소요일은 1.5 일/km로 설정하였다.[30] 따라서 본 연구의 최적화 목적함수는 아래와 같이 설정하였다.
| (11) |
3. 연속적 개미 군집 최적화 알고리즘
개미 군집 최적화(ACO)는 실제 개미들이 먹이를 찾는 과정에서 보이는 집단적 행동을 모방하여 이산적 문제에서 경로를 탐색하기 위해 개발된 메타 휴리스틱 최적화 알고리즘의 일종이다.[31,32] 한편, ACO로부터 확장된 연속적 개미 군집 최적화(CACO)는 경로뿐만 아니라 다양한 변수를 동시에 고려하기 위해 가우스 확률밀도함수를 이용하여 해의 탐색 경로를 연속적인 해 공간에서 찾는 기법이다.[33]
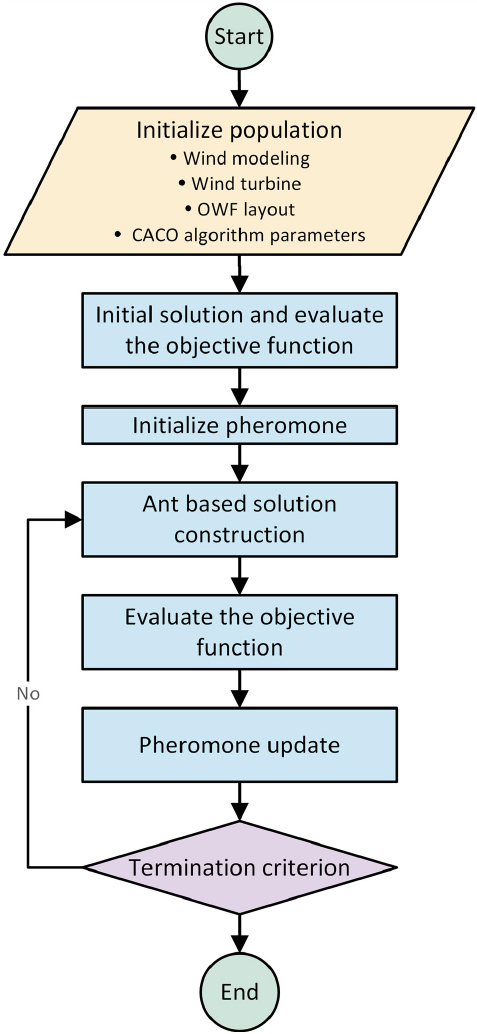
본 연구에서 WT의 위치를 최적화하여 전력 생산량을 극대화하고, 설치 비용을 최소화하는 것을 목표로 한다. OWF는 해상 환경의 특성상 변수와 제약 조건이 많고 복잡한 최적화가 필요하므로 CACO를 활용한다. 특히, CACO는 무작위성을 기반으로 탐색하는 방식으로 국지적 최적해에 빠지지 않으면서도 전역 최적해를 탐색하는 장점이 있다. Fig. 6은 CACO 알고리즘의 순서도이다.
초기화 단계에서는 모집단인 개미의 숫자, 최적화 세대수, WT과 OWF의 설계 변수, 종료 조건 등을 정의한다. 그리고 균일 난수 생성을 통해 개미의 초기 배치를 수행하고 결과를 바탕으로 최적화 목적함수를 평가한다.
각 개미는 연속적 가우스 확률분포, 식 (8)에 따라 연속적 해 공간에서 개미 기반 최적 배치 해를 생성한다.
| (12) |
여기서, 각 해 sl은 성능에 따라 순위가 매겨지며, 순위가 동일할 때는 무작위로 결정된다. 해는 순위 l에 따라 가중치 ωl가 정해진다. qσ가 작을 때, 높은 순위(낮은 l)의 해가 강하게 선호되며, 클 때는 가중치 분포가 균일해지며, 모든 해가 선택될 확률이 비슷해진다. Kp는 모집단(Population)의 수이다.[33]
최적화 과정에서 해의 적합도가 높은 배치가 선택될 확률을 높이고 국지적 해에 빠지지 않기 위해 룰렛 휠(Roulette Wheel) 선택을 활용한다.
새로운 해에 대해 최적화 함수를 평가하고 적합도를 바탕으로 페로몬을 업데이트한다. 이때, 해의 적합도가 우수하면 페로몬을 남겨 다음 반복에서 그 해가 탐색되도록 유도한다.
| (13) |
여기서, 식 (13)의 는 i 세대 해의 표준편차이며, 탐색 범위의 크기를 결정한다. s는 임의 해이고 ξ는 새로운 해를 탐색할 때, 탐색 범위를 조절하는 매개변수이다. 알고리즘의 종료 조건에 도달하면 해의 탐색을 종료하고 그 결과를 출력한다.
3.1 수치해석 개요
본 연구에서는 NREL 15 MW급 RWT 67기(총 1 GW급)로 구성된 부유식 OWF의 WT 배치 최적화를 수행한다. 그리고 최적화 알고리즘 CACO를 적용하기 위해 모집단의 수(개미 수)를 배치 WT 수의 4배수(268개)로 설정하고, 세대수를 500세대로 한다. 해의 탐색 범위를 조절하는 ξ는 1로 고정하고, qσ는 10-2, 10-4로 2가지로 설정하였다. 각각의 계산은 10회씩 반복하여 결과를 도출하여 최적의 배치를 최종 선정한다.
최적화 목적함수를 구성하는 케이블의 비용을 구하기 위해 WT를 사이클이 존재하지 않도록 한 번씩만 연결하는 동시에 최소 길이로 연결하는 최소 신장 트리(MST)의 프림 알고리즘(Prim’s algorithm)을 활용하였다.[34]
4. 해상풍력단지 최적 배치 결과
4.1 단순 배치 결과
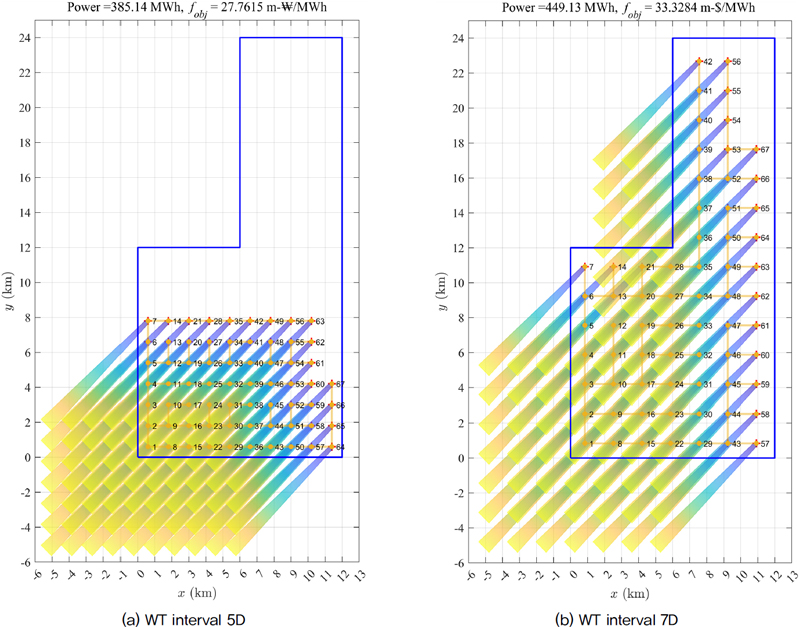
15 MW급 WT 67기로 구성된 1 GW급 OWF를 배치 최적화 결과와 비교를 위해 우선 WT 간격을 5D와 7D로 설정하여 격자 배치하여 평균 전력 생산량을 도출하였다. 전력 생산량은 Table 1의 풍향별 바람 발생 빈도와 평균 풍속, 식 (7)의 후류를 고려한 임의의 WT i로 유입되는 풍속과 전력 생산량 식 (9)를 이용하여 도출한다. 또한, WT을 최소 길이로 연결하여 그 연결 길이는 최소 신장 트리 알고리즘을 활용하여 구하였다. Fig. 7은 주풍향(NE)에 대해 후류를 나타낸 것으로, 후류의 길이는 식 (5)를 이용하여 후류의 풍속이 교란되지 않은 유입 풍속 v0이 90% 회복되는 하류 거리를 구해 얻은 35D로 설정하였다. 또한, 후류의 확장 크기는 후류 확장비 α(Fig. 4 참조)를 활용하여 이론적인 후류의 크기를 모사한 결과이다.
Fig. 7(a)는 OWF 영역 내에서 WT 간격을 5D(= 1,200 m)로 설정하여 총 WT 67기를 배치한 결과이다. 본 배치의 결과, 평균 전력 생산량은 385.14 MWh, WT간 최소 연결 길이는 79.2 km이며, 케이블 연결 비용은 10,692 백만원으로 최적화 목적함수(1 MWh당 케이블 부설 비용)는 27.7615 백만원/MWh이다.
Fig. 7(b)는 같은 OWF 영역 내에, WT 간격을 7D (=1,680 m)로 설정하여 총 67기의 WT를 배치한 결과이다. WT 간격이 커지면서 후류로 인한 발전량 저하가 감소하여 평균 전력 생산량은 5D 배치 간격의 결과보다 16.6% 증가한 449.13 MWh이다. 또한, 배치 간격의 증가로 인해, 케이블 연결 길이는 110.88 km, 케이블 연결 비용은 14,968.8 백만원으로 증가하여 1 MWh당 케이블 부설 비용은 33.3284 백만원/MWh으로 증가하였다.
4.2 배치 최적화 결과
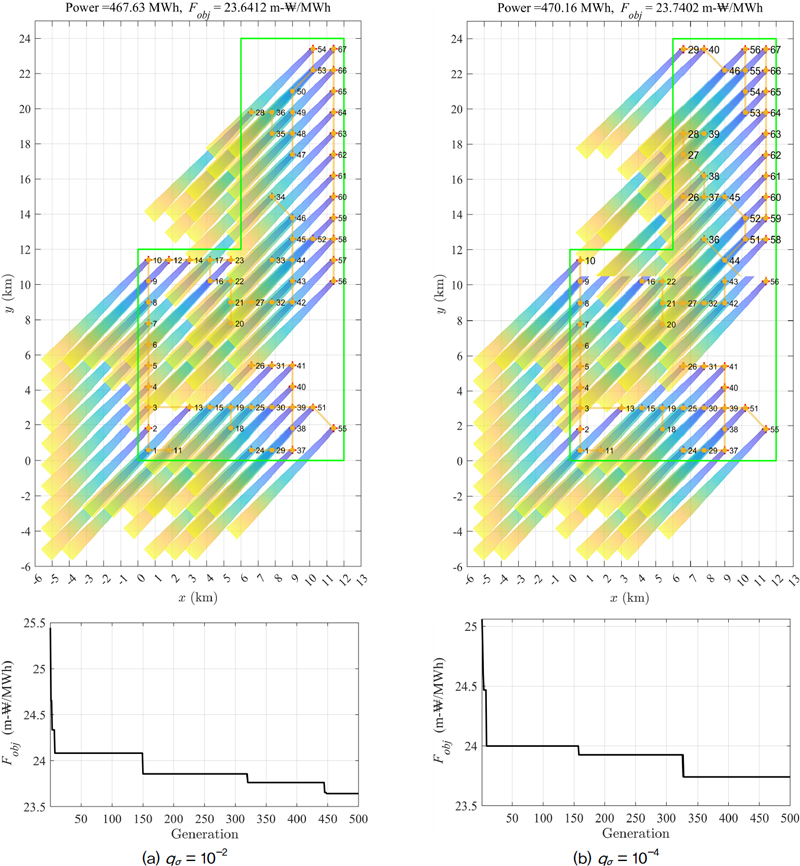
Fig. 8은 OWF 영역 내의 150개의 배치 격자 중 CACO 최적화를 통해 얻은 WT 67기의 최적 배치 결과와 세대에 따른 최적화 목적함수의 수렴도를 나타낸다. Fig. 8(a)는 비교적 큰 qσ값을 사용하여 얻은 결과이며, 평균 전력 생산량이 467.63 MWh이고, WT간 최소 연결 길이는 81.89 km, 케이블 연결 비용은 11,055.3 백만원으로 최적화 목적함수는 23.6412 백만원/MWh이었다.
비교적 작은 qσ=10-4을 사용하여 CACO를 수행한 Fig. 8(b)의 최적 배치 결과는 평균 전력 생산량이 470.16 MWh이고, WT간 최소 케이블 연결 길이는 82.68 km, 케이블 부설 비용은 11,161.7백만원으로 최적화 목적함수 23.7402 백만원/MWh이었다.
4.3 수치해석 결과 및 고찰
일반적으로 OWF의 배치는 일정한 터빈 간격에서 사각형 격자 배열이 많이 활용된다. 이러한 배열은 터빈 간 거리의 최적화를 통해 후류의 영향을 최소화할 수 있고, 직관적이고 대칭적 배열을 통해 단지 설계를 단순화할 수 있어 터빈에 접근이 쉬워 유지보수 측면에서도 유리하다. 본 연구에서도 Fig. 7의 결과와 같이 격자형 단지의 배치는 배열이 단순하고, 터빈의 간격을 증가할수록 단지의 평균 전력 생산량이 증가하는 결과를 확인할 수 있었다.
한편, 최적화 알고리즘을 활용하여 5D 간격으로 배치된 총 150개의 후보 중 최적의 67기 배치를 도출한 Fig. 8(a)의 결과를 보면, 평균 전력 생산량은 Fig. 7(a)와 비교해 21.4% 증가하였다. 이 경우 OWF 전체 영역을 활용했음에도, WT 간 최소 연결 길이는 단 3.4% 증가에 그쳤다. Fig. 8(b)의 경우, 평균 전력 생산량이 22.1% 증가했으며, 케이블 연결 길이는 4.4% 증가하는 것으로 나타났다.
Fig. 8의 세대수에 따른 최적화 목적함수 값의 수렴 특성을 살펴보면, qσ이 작은 Fig. 8(b)가 수렴이 빠르고 더 우수한 결과를 도출하였다. 이는 3장에서 언급한 바와 같이, qσ이 작을수록 해의 순위가 높은 해에 큰 가중치를 부가하여 빠른 해의 수렴을 보이는 CACO의 특징과 잘 일치하였다.[33]
한편, 부유식 해상풍력발전단지의 비용 구성 요소로는 하부 구조 및 기초, 터빈, 전기 인프라, 조립 및 설치, 운영 및 유지보수, 임차 등이 있다. 최적의 배치를 위해서는 이러한 모든 요소를 동시에 고려해야 하지만, 이 과정에서 계산량이 기하급수적으로 증가한다. 이에 따라 본 연구에서는 배치 결과에 영향을 받지 않는 고정 비용은 제외하고, 최적화 결과에 따라 달라질 수 있는 내부 케이블 최소 길이와 그에 따른 설치 비용만을 고려하였다. 본 연구에서 제시한 비용 함수는 배치 최적화를 위한 용도로만 활용되었으며, 실제 단지 설계 시에는 별도의 정밀한 비용 산출이 필요하다.
5. 결 론
본 연구는 친환경 해양그린수소 발전을 위한 전력의 안정적 공급을 목표로, 1 GW급 해상풍력발전단지의 풍력터빈 배치 최적화를 수행한 기초 연구이다. 이를 위해 동해 가스전 인근 해역을 대상 해역으로 선정하고, 바람 자원 분석에는 NASA의 MERRA-2 재해석 데이터를 활용하였다. 풍향별 바람 발생 빈도를 고려하여 Jensen의 후류 모델을 사용해 단지의 전력 생산량을 산출하고, 터빈 간 최소 연결 거리를 계산하여 케이블 설치 비용을 평가하였다. 이를 통해 최소 케이블 길이로 인한 설치 비용 대비 최대 전력 생산량을 목표로 하는 최적화 목적함수를 구성하였다. 최적화 과정에는 연속적 개미 군집 최적화 알고리즘을 적용하여 풍력터빈 배치를 최적화하였다.
그 결과, 일정한 터빈 간격을 가진 격자 배열의 단순 배치에 비해서 배치 최적화를 수행한 단지의 전력 생산량이 20% 이상 증가하는 것을 확인 할 수 있었다. 따라서 연속적 개미 군집 최적화 알고리즘을 활용한 신재생에너지 해상플랫폼의 최적 배치 설계 반영 가능성을 엿볼 수 있었다.
국내 부유식 해상풍력발전단지의 경우, 아직 비용 산출에 필요한 근거 자료가 부족한 실정이다. 따라서 후속 연구를 통해 생산 전력의 송배전과 관련된 해상 변전소 건설 비용, 계통 연계 비용, 운영 및 유지보수 비용 등을 포함한 실질적인 비용 산출 방식이 마련되어야 한다. 이 과정에서 해저 지형을 고려하여 터빈의 계류 특성을 반영한 연구가 요구되며, 효율적인 최적화 알고리즘의 적용과 요잉으로 인한 실질적인 후류 영향을 구속 조건에 반영하는 것도 필요하다. 이러한 연구를 통해 친환경 해양그린수소 발전을 위한 부유식 해상풍력발전단지의 설계 기초 자료를 제공할 수 있을 것으로 기대된다.
Nomenclature
| Aij : | wake overlapped area, m2 |
| Cclv : | cost of cable laying vessel, m-₩/day |
| Cin–cbl : | cost of in-field cables, m-₩ |
| Fobj : | optimization objective function, m-₩/MWh |
| Lin–cbl : | total length of in-field cables, km |
| POWF : | power production of OWF, MWh |
| : | average power production of OWF, MWh |
| Rr : | radius of rotor |
| Wr : | radius of wake zone, m |
| k : | shape parameter |
| rd : | daily cable laying length, day/km |
| vd : | incident wind speed, m/s |
| vH : | wind speed at hub height, m/s |
| vref : | reference velocity, m/s |
| z0 : | surface roughness length, m |
| zH : | hub height, m |
| zref : | reference height, m |
| α : | wake decay coefficient(=0.5ln(zH/z0)) |
| γ : | location parameter, m/s |
| θ : | coordinate C.C.W. rotation angle, deg |
| θd : | wind direction, deg (=3π/2–θ) |
| λ : | scale parameter, m/s |
| ρ : | air density, kg/m3 |
| σ : | power law exponent |
Subscript
| ACO : | ant colony optimization |
| CACO : | continuous ant colony optimization |
| MST : | minimum spanning tree |
| OWF : | offshore wind farm |
| RWT : | reference wind turbine |
| WT : | wind turbine |
Acknowledgments
본 논문은 해양수산부 재원으로 선박해양플랜트연구소의 주요사업인 “대용량 집중형 해양그린수소 생산 저장 해상플랫폼 기술개발”(PES5546)과 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원(RS-2022-KP002820)을 받아 수행되었습니다.
References
- Poshydon, 2024, “About PosHYdon”, Accessed 11 November 2024, https://poshydon.com/en/home-en/about-poshydon/, .
- RWE, 2024, “H2opZee”, Accessed 11 November 2024, https://www.rwe.com/en/research-and-development/hydrogen-projects/h2opzee/, .
- Federal Ministry of Education and Research, 2024, “H2Mare: offshore”, Accessed 11 November 2024, https://www.wasserstoff-leitprojekte.de/projects/h2mare, .
-
Lee, J.S., Son, W.J., Lee, B.K., and Cho, I.S., 2019, “Optimal site selection of floating offshore wind farm using genetic algorithm”, J. Korean Soc. Mar. Environ. Saf., 25(6), 658-665.
[https://doi.org/10.7837/kosomes.2019.25.6.658]

-
Kim, J.H., Jung, J.H., and Kim, B.S., 2017, “Optimal arrangement of multiple wind turbines on an offshore wind-wave floating platform for reducing wake effects and maximizing annual energy production”, Korea Soc. Mar. Eng. Tech., 41(3), 209-215.
[https://doi.org/10.5916/jkosme.2017.41.3.209]

-
Park, R.J., Kang, S., Lee, J., and Jung, S., 2022, “CNNLSTM based wind power prediction system to improve accuracy”, New. Renew. Energy, 18(2), 18-25.
[https://doi.org/10.7849/ksnre.2022.0001]

-
Lee, S., Kim, S., and Kim, B., 2024, “Effect of wind-wave misalignment and yaw error on power performance and dynamic response of 15 MW floating offshore wind turbine”, New. Renew. Energy, 20(2), 26-34.
[https://doi.org/10.7849/ksnre.2024.0013]

-
Kim, H.K., Han, W.S., and Lee, S.G., 2019, “Wind farm layout optimization considering dynamic characteristic of floating wind turbine”, New. Renew. Energy, 15(3), 1-10.
[https://doi.org/10.7849/ksnre.2019.9.15.3.001]

-
Park, S., Kim, K.H., Lee, K.S., Park, Y.S., Oh, H., Shin, H., and Hong, K., 2015, “Arrangement design and performance evaluation for multiple wind turbines of 10MW class floating wave-offshore wind hybrid power generation system”, J. Korean Soc. Mar. Env. and Energy, 18(2), 123-132.
[https://doi.org/10.7846/JKOSMEE.2015.18.2.123]

-
Han, W.B., Lee, K.H., and Lee, S.J., 2024, “Wave analysis method for offshore wind power design suitable for suitable for Ulsan area”, New. Renew. Energy, 20(2), 2-16.
[https://doi.org/10.7849/ksnre.2024.0011]

- Kim, J.C., Kim, M.J., and Paek, I.S., 2020, “Development of an in-house code for layout optimization of offshore wind farms”, Journal of Wind Energy, 11(4), 54-64.
-
Choi, N.J., Nam, S.H., Jeong, J.H., and Kim, K.C., 2011, “CFD study on aerodynamic power output of 6 MW offshore wind farm according to the wind turbine separation distance”, J. Korean Soc. Mar. Eng., 35(8), 1063-1069.
[https://doi.org/10.5916/jkosme.2011.35.8.1063]

- Royal Haskoning DHV., 2021, “East Anglia TWO offshore windfarm - windfarm layout principles statement”, Scottishpower Renewables, 1-9, https://infrastructure.planninginspectorate.gov.uk/wp-content/ipc /uploads/projects/EN010078/EN010078-004517-ExA.AS-34.D8.V1%20EA2%20Layout%20Principles%20Statement.pdf, .
- Google Earth, 2015, “Donghae gas platn 35°20'43"N, 129°50'29"E”, 3D Buildings data layer, https://earth.google.com/web, .
- NASA Earthdata, Goddard Earth Sciences Data and Information Services Center (GES DISC), 2024, “Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2)”, Accessed October 13, 2024, https://disc.gsfc.nasa.gov, .
- International Electrotechnical Commission (IEC), 2019, “IEC 61400-3-1: Wind Turbines-Part 3-1: Design requirements for offshore wind turbines”, 1st Edition, Geneva.
- Byun, D.S., Kim, H.W., Lee, J.Y., Lee, E.I., Park, K.A., and Woo, H.J., 2018, “Converting Ieodo ocean research station wind speed observations to reference height data for real-time operational use”, The Sea: J. Korean Soc. Oceanogr., 23(4), 153-178.
-
Hsu, S.A., Meindl, E.A., and Gilhousen, D.B., 1994, “Determining the power-law wind-profile exponent under near-neutral stability conditions at sea”, J. Appl. Meteorol., 33(6), 757-765.
[https://doi.org/10.1175/1520-0450(1994)033<0757:DTPLWP>2.0.CO;2]

-
Seo, B.K., Kim, Y.H., Kim, J.H., and Kim, B.J., 2017, “Comparison of wind resource characteristics in Korea according to different mapping method”, New. Renew. Energy, 13(4), 23-38.
[https://doi.org/10.7849/ksnre.2017.12.13.4.023]

- National Renewable Energy Laboratory (NREL), 2020, “2020 Annual Technology Baseline: Offshore Wind”, Golden, CO: National Renewable Energy Laboratory, Accessed 13 October, 2024, https://nrel.github.io/turbine-models/2020ATB_NREL_Reference_15MW_240.html, .
- Katic, I., Højstrup, J., and Jensen, N.O., 1987, “A simple model for cluster efficiency”, Proc. Eur. Wind Energy Assoc. Conf. Exhib., 1, 407-410.
-
Du Pont, B.L., and Cagan, J., 2012, “An extended pattern search approach to wind farm layout optimization”, J. Mech. Des., 134(8), 081002.
[https://doi.org/10.1115/1.4006997]

-
Feng, J., and Shen, W.Z., 2015, “Solving the wind farm layout optimization problem using random search algorithm”, Renewable Energy, 78, 182-192.
[https://doi.org/10.1016/j.renene.2015.01.005]

-
Ju, X., and Liu, F., 2019, “Wind farm layout optimization using self-informed genetic algorithm with information guided exploitation”, Appl. Energy, 248, 429-445.
[https://doi.org/10.1016/j.apenergy.2019.04.084]

- Kim, M.J., Song, Y., and Paek, I., 2020, “Development of an in-house code to predict annual energy production and economic analysis of wind farms using CFD results”, Journal of Wind Energy, 11(3), 23-30.
- Rathmann, O.S., Hansen, B.O., Hansen, K.S., Mortensen, N.G., and Murcia Leon, J.P., 2018, “The Park2 wake model-documentation and validation”, DTU Wind Energy E, 160, 1-25, https://backend.orbit.dtu.dk/ws/portalfiles/portal/151671395/Park2_Documentation_and_Validation.pdf, .
-
Manwell, J.F., Mcgowan, J. G., and Rogers, A. L., 2009, “Wind characteristics and resources, in : Wind Energy Explained Theory”, Design and Application, (2nd eds.), John Wiley & Sons Ltd., West Sussex, 45-46.
[https://doi.org/10.1002/9781119994367]

-
Kirchner-Bossi, N., and Porté-Agel, F., 2024, “Wind farm power density optimization according to the area size using a novel self-adaptive genetic algorithm”, Renewable Energy, 220, 119524.
[https://doi.org/10.1016/j.renene.2023.119524]

-
Stehly, T., and Duffy, P., 2022, “2021 cost of wind energy review”, National Renewable Energy Laboratory, 1-65, https://www.nrel.gov/docs/fy23osti/84774.pdf, .
[https://doi.org/10.2172/1907623]

-
Lerch, M., De-Prada-Gil, M., and Molins, C., 2021, “A metaheuristic optimization model for the inter-array layout planning of floating offshore wind farms”, Int. J. Electr. Power Energy Sys., 131, 107128.
[https://doi.org/10.1016/j.ijepes.2021.107128]

- Dorigo, M., 1992, “Optimization, learning and natural algorithms(in Italian)”, Ph.D. thesis, Dipartimento di Elettronica, Politecnico di Milano, Italy.
-
Dorigo, M., Birattari, M., and Stutzle, T., 2006, “Ant colony optimization”, in IEEE Comput. Intell. Mag., 1(4), 28-39.
[https://doi.org/10.1109/CI-M.2006.248054]

-
Socha, K., and Dorigo, M., 2008, “Ant colony optimization for continuous domains”, Eur. J. Oper. Res., 185(3), 1155-1173.
[https://doi.org/10.1016/j.ejor.2006.06.046]

- MathWorks, 2024, “MATLAB Release R2024a”, Natick, Massachusetts: The MathWorks, Inc.