The Korean Society For New And Renewable Energy

[ Article ]

New & Renewable Energy - Vol. 21, No. 1, pp.2-11

ISSN: 1738-3935 (Print) 2713-9999 (Online)

Print publication date 25 Mar 2025

Received 04 Feb 2025 Revised 24 Feb 2025 Accepted 27 Feb 2025

DOI: https://doi.org/10.7849/ksnre.2025.0003

전산유체역학을 활용한 시멘트 제조 공정의 염소 바이패스 시스템 최적화 연구

전지민¹⁾

; 임정환²⁾

; 오세천³⁾^{, *}

; 김재형⁴⁾

; 김우태⁵⁾

; 최규성⁶⁾

Optimization of the Chlorine Bypass System in the Cement Manufacturing Process Through Computational Fluid Dynamics

Jimin Jeon¹⁾

; Junghwan Im²⁾

; Seacheon Oh³⁾^{, *}

; Jaehyung Kim⁴⁾

; Wootae Kim⁵⁾

; Kyusung Choi⁶⁾

1)Master’s Student, Department of Environmental Engineering, Kongju National University
2)Undergraduate Student, Department of Environmental Engineering, Kongju National University
3)Professor, Department of Environmental Engineering, Kongju National University
4)Master’s Student, Department of Mechanical and Automotive Engineering, Kongju National University
5)Professor, Department of Mechanical and Automotive Engineering, Kongju National University
6)Deputy General Manager, SsangYong C&T Corporation

Correspondence to: ^*

© 2025 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The cement industry is an energy-intensive and carbon-emitting sector, highlighting the increasing importance of greenhouse gas reduction strategies and the development of related technologies to achieve carbon neutrality. Greenhouse gas emissions from the cement manufacturing process can be classified into process emissions, direct emissions, and indirect emissions. Among these, direct emissions resulting from fuel combustion can be mitigated by substituting conventional bituminous coal with alternative fuels such as waste synthetic resin. However, waste synthetic resins contain chlorine, which can adversely affect the manufacturing process and cement quality. To minimize these negative impacts, the chlorine bypass (CBP) system is essential. The bypass ratio is proportional to the fuel substitution rate, and when the substitution rate exceeds 65%, a bypass ratio of 12% is required to maintain an appropriate chlorine concentration in the kiln under the carbon neutrality roadmap. This study employed computational fluid dynamics to determine the optimal probe design conditions for a CBP system capable of efficiently processing 12% of the extracted gas. The proposed design is expected to facilitate the expansion of waste synthetic resin fuel utilization and contribute to the reduction of greenhouse gas emissions.

Keywords:

Cement manufacturing process, Alternative fuel, Waste synthetic resin, Chlorine by-pass system, Computational fluid dynamics

키워드:

시멘트 제조 공정, 대체 연료, 폐합성수지, 염소 바이패스 시스템, 전산유체역학

1. 서 론

기후 위기에 대응하기 위해 국제사회는 파리협정을 채택하였으며, IPCC(International Panel on Climate Change)는 2050년까지 탄소중립 달성을 목표로 제시하였다. 이에 따라 대한민국은 ‘2050 탄소중립 시나리오’를 수립하고, 국제 동향과 국내 감축 여건을 고려하여 2030 국가 온실가스 감축목표(NDC, Nationally Determined Contribution)를 상향 조정하였다. NDC는 탄소중립 실현을 위한 중간 단계로, 2018년 국내 온실가스 배출량 727.6백만 톤을 기준으로 2030년까지 436.6백만 톤으로 감축하여 40% 이상의 감축률을 달성하는 것을 목표로 한다.^[1~3]

국내 시멘트 산업은 철강 및 석유화학 산업에 이어 에너지 소비와 탄소 배출량이 많은 주요 산업으로 분류되며, NDC에 따라 2018년 대비 2030년까지 온실가스 배출량을 12% 감축해야 한다. 이에 따라 시멘트 산업의 온실가스 감축 전략 및 목표 설정에 대한 중요성이 부각되고 있다. 시멘트 제조 공정에서 발생하는 온실가스는 원료의 탈탄산 반응에 기인한 공정 배출, 연료 연소 반응에서 기인한 직접 배출, 전력 사용 및 운송 과정에서의 간접 배출로 구분된다. 이 중 직접 배출은 시멘트 산업 전체 배출량의 33%를 차지하고 있으며, 유연탄 등의 화석연료를 폐합성수지 등의 순환자원으로 전환함으로써 배출량을 감축할 수 있다.^[1,4] 하지만 2021년 기준 국내 평균 연료 대체율은 35%로 EU 평균치인 53%에 비해 낮은 수준이며, 폐합성수지에는 염소 성분이 다량 함유되어 있어 연료 대체에 한계가 있다.^[5] 폐합성수지의 염소 성분을 비롯한 황산염, 알칼리 등 휘발성 화합물은 낮은 융점으로 인해 소성로에서 유입되는 약 1,200°C의 가스에 의해 휘발되며 가스 흐름에 따라 온도가 낮은 예열기로 이동하면서 응축된다. 응축된 화합물은 다시 휘발되는 순환 과정을 반복하며 설비 내벽에 코팅을 형성한다. 이러한 거동은 원료 및 가스 흐름을 방해하고 설비를 부식시키는 등 공정 불안정 및 시멘트 품질 저하를 초래한다. 따라서 휘발성 화합물의 축적을 방지하고 공정을 안정화하기 위한 기술 개발이 필요하다.^[6~9]

염소 바이패스(CBP, Chlorine By-Pass) 시스템은 휘발성 화합물을 효과적으로 제어하여 예열기 내 코팅 형성을 최소화하는 데 널리 활용되는 기술이다. CBP 시스템은 일반적으로 프로브(Probe), 사이클론(Cyclone), 냉각기(Cooler), 백 필터(Back Filter) 등으로 구성되며, 프로브를 휘발성 화합물이 고농도로 존재하며 더스트 비산량이 적은 지점에 설치하여 소성로 배기가스를 추출한다. 추출된 가스는 냉각 공기와의 혼합을 통해 융점 이하의 온도로 신속히 냉각되어 입자 형태로 처리된다. 이후 사이클론에서 염소 농도가 상대적으로 낮은 조립자는 분리되어 소성로로 반환되고, 미립자는 백 필터에서 처리된다.^[10~12] CBP 시스템의 바이패스율은 연료 대체율에 비례하며, 2050 탄소중립 시나리오에 따라 폐합성수지 연료 대체율이 60% 이상으로 증대될 경우^[13] 소성로 내 제한된 염소 농도를 유지하기 위해 약 10%의 바이패스율이 요구된다. 이는 선행 연구에서 Weber 모델을 기반으로 도출된 값으로,^[14] 본 연구에서는 여유율을 고려하여 12%의 바이패스율을 목표로 설정하였으며, 이를 경제적으로 처리하기 위한 최적의 프로브 개발이 필요하다. 프로브는 추기 가스의 고온 영역을 신속히 냉각하여 사이클론 및 백 필터에서의 처리가 용이하도록 설계되어야 하며, 고온 및 부식 환경에서도 안정적인 운영이 가능하도록 설비의 내구성을 확보해야 한다.^[6]

본 연구는 프로브의 성능 최적화를 목표로 내부 가스 유동 및 열전달 특성에 대한 전산유체역학(CFD, Computational Fluid Dynamics) 해석을 수행하였다. CFD는 실험으로 구현하기 어려운 시스템을 분석할 수 있는 도구로써 다양한 연구 조건에서 결과를 도출하는 데 유리하다.^[15] 이에 따라 본 연구에서는 CFD를 활용하여 프로브의 냉각 효율 및 압력 손실을 개선하기 위한 설계 요소를 세부적으로 분석하였다. 이를 바탕으로 바이패스율 12%를 충족하는 최적의 프로브 설계 조건을 제안하였으며, 지속 가능한 시멘트 제조 공정을 위한 기술적 해결책을 제시하였다.

2. 수치 해석 방법

2.1 해석 형상

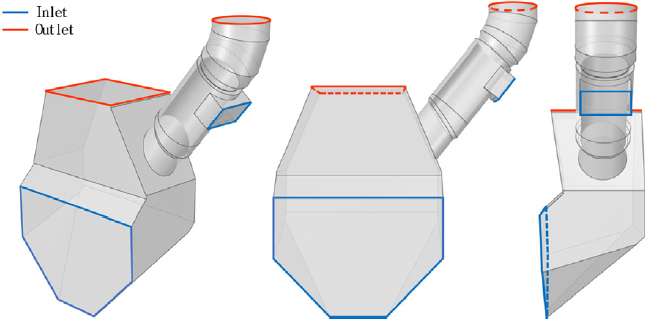
CFD 해석에 사용된 형상은 Fig. 1에 제시된 바와 같이 소성로의 Rising Duct 측면에 프로브가 경사 형태로 장착된 구조를 기반으로 한다. 프로브는 내관 및 외관으로 구성된 이중관 구조이며, 외관을 통해 유입된 냉각 공기는 먼저 내관의 표면 온도를 감소시킨 후 하단으로 토출되어 추기 가스와 혼합됨으로써 냉각이 이루어지도록 설계되었다. 이러한 이중 냉각 방식은 냉각 효율을 향상시키는 데 기여하며, 이중관 구조는 프로브 냉각 효율의 주요 설계 인자로 작용한다. 본 연구에서는 이중관 지름이 내부 유동장에 미치는 영향을 분석하기 위해 내관의 내경 및 외경, 외관의 내경 크기를 조합하여 총 아홉 가지의 설계 Case를 도출하였다. 내관의 내경은 각각 1143.33 mm, 1114.86 mm, 1087.65 mm로 설계하고 내관의 외경은 설비 두께인 14 mm를 고려하여 산정되었다. 또한, 내관과 외관 사이의 단면적을 다르게 설정하여 외관의 내경을 조정하였으며, 이를 통해 냉각 공기 토출구 간격의 영향을 분석하고자 하였다. 따라서 내관과 외관 사이의 단면적은 Case 1, 2, 3에서 0.51 m², Case 4, 5, 6에서는 0.46 m², 그리고 Case 7, 8, 9에서는 0.41 m²로 설계되었다. Case 1에서 6까지는 동일한 가스 체류 시간 조건에서 내관과 외관 사이의 단면적이 미치는 영향을 조사하고자 하였으며, Case 7에서 9까지는 최소 단면적 크기로 인한 유속 변화를 고려하여 가스 체류 시간을 단축하였을 때의 영향을 검토하고자 하였다. 이에 따라 가스 체류 시간은 Case 1, 2, 3, 4, 5, 6에서 0.03 s, Case 7, 8, 9에서는 0.02 s로 적용되었으며, 추기되는 가스 체적 유량은 동일하므로 이중관의 길이를 조정하였다. 각 설계 조건은 Table 1에 정리하였다.

Fig. 1.

Geometry

Table 1.

Double-Tube conditions

2.2 격자

본 연구에서는 Fluent Meshing을 활용하여 격자를 생성하였으며, 계산 비용을 고려하여 격자 조밀도 및 셀(Cell) 개수를 조정한 동일한 조건을 적용하였다. 격자의 품질은 격자의 왜곡 정도를 나타내는 Skewness와 셀의 직교성을 나타내는 Orthogonal을 주요 지표로 평가하였다. 해석의 정확성 및 수렴성을 향상시키기 위해 Skewness는 최대 0.75 이하, Orthogonal은 최소 0.1 이상의 값이 요구되며, Table 2로부터 본 연구에서 생성된 격자의 Skewness 및 Orthogonal 값은 각각 양호한 범위에 포함되어 있음을 확인할 수 있다.^[15~18]

Table 2.

Grid information of Case 1~9

2.3 해석 모델

내부 가스 흐름 및 열전달 등 관련 현상을 모델링하기 위해 상용 CFD 프로그램인 Ansys Fluent 2022 R2를 활용하였다. Ansys Fluent는 모든 유동에 대해 질량 및 운동량 보존 방정식을 계산하며, 열전달 또는 유동이 난류인 경우 에너지 보존 방정식 및 추가 수송 방정식을 계산한다. 다음의 식은 본 연구에서 사용한 질량 보존 방정식 (1), 운동량 보존 방정식 (2), 에너지 보존 방정식 (3)을 나타내며, 난류로 인하여 유동 내 복잡한 상호작용이 일어나는 eddy를 해석하기 위해 레이놀즈 평균 Navier-Stokes(RANS) 방정식 (4), (5)를 사용하여 난류 유동 계산을 수행하였다.^[17]

∂ ρ ∂ t + ∇ ⋅ ρ v → = S m

(1)

∂ ∂ t ρ v → + ∇ ⋅ ρ v → v → = - ∇ p + ∇ ⋅ τ - ¯ + ρ g → + F → = ∇ ⋅ k e f f ∇ T - ∑ j h j J j → + τ - ¯ e f f v → + S h

(2)

∂ ∂ t ρ e + v 2 2 + ∇ ⋅ ρ v → h + v 2 2

(3)

∂ ρ ∂ t + ∂ ∂ x i ρ u i = 0

(4)

∂ ∂ t ρ u i + ∂ ∂ x j ρ u i u j = - ∂ p ∂ x i + ∂ ∂ x j μ ∂ u i ∂ x j + ∂ u j ∂ x i - 23 δ i j ∂ u l ∂ x l + ∂ ∂ x j - ρ u i' u j' ¯

(5)

RANS 방정식에 의한 난류 계산이 가능하도록 하기 위해서는 레이놀즈 응력 $- ρ u i' u j' ¯$ 과 추가적인 스칼라 수송항을 예측하는 난류 모델이 필요하다. 본 연구에서 채택한 난류 모델은 Ansys Fluent의 standard k-ε 모델이며, 이 모델은 난류 운동 에너지(k) 및 에너지 소산율(ε)에 대한 모델 수송 방정식 (6), (7)을 기반으로 기술된다.^[17,19]

∂ ∂ t ρ k + ∂ ∂ x i ρ k u i = ∂ ∂ x j μ + μ t σ k ∂ k ∂ x j + G k + G b - ρ ϵ - Y M + S k

(6)

∂ ∂ t ρ ϵ + ∂ ∂ x i ρ ϵ u i = ∂ ∂ x j μ + μ t σ ϵ ∂ ϵ ∂ x j + C 1 ϵ ϵ k G k + C 3 ϵ G b - C 2 ϵ ρ ϵ 2 k + S ϵ

(7)

2.4 해석 조건

입구와 출구는 각각 velocity-inlet과 pressure-outlet 조건으로 설정하였으며, 이에 대한 압력-속도 결합 알고리즘은 SIMPLEC를 사용하였다. 해석에 적용된 경계 조건은 현장 측정값을 참고하였으며, 설정값은 Table 3에 정리하였다. Rising Duct로 유입되는 가스의 속도는 표준 체적 유량을 온도 및 압력을 고려한 실제 체적 유량으로 환산하여 산출되었다. 냉각 공기의 속도는 20°C의 냉각 공기와 1,200°C의 추기 가스가 혼합되어 500°C로 냉각되는 경우의 열평형 방정식을 이용하여 계산되었다. 프로브 출구에서 요구되는 게이지 압력은 이중관의 크기에 따라 상이하게 나타날 수 있으며, 바이패스율 12%를 충족하는 동일 조건에서 해석 결과를 비교하기 위해 Rising Duct 출구의 압력을 고정된 값으로 설정하고 프로브 출구의 압력을 반복 계산하여 각 Case에 적합하도록 조정하였다. 본 연구에서는 Rising Duct 출구의 체적 유량이 입구 체적 유량의 88%에 도달할 경우 바이패스율 12%가 충족된 것으로 간주하였으며, 이는 Ansys Fluent에서 프로브 출구의 평균 온도를 면적 가중 평균 방식으로 계산하는 과정에서 체적 유량 산출 시 발생할 수 있는 오차를 고려한 것이다.^[20] 따라서 온도가 일정한 Rising Duct 출구를 기준으로 바이패스율을 계산함으로써 결과의 신뢰성을 확보하였다.

Table 3.

Boundary conditions

3. 수치 해석 결과

Rising Duct 입구로 유입되는 가스 체적 유량은 약 60.8698 Nm³/s이며, 이 중 12%가 바이패스되는 경우 이론적으로 Rising Duct 출구에서의 가스 체적 유량은 약 53.5655 Nm³/s로 계산된다. 실제 공정 운영에서는 12% 바이패스율을 충족하기 위해 ID(Induced Draft) Fan을 이용하여 가스를 추출하며, 본 연구에서는 Fluent 계산 과정에서 Rising Duct 출구의 체적 유량 변화를 모니터링하여 이중관 구조에 따라 12% 바이패스 조건을 충족할 수 있도록 프로브 출구의 게이지 압력을 설정하였다. Table 4에 각 Case에 대한 프로브 출구 압력 조건 및 이에 따라 측정된 Rising Duct 출구 체적 유량 값을 정리하였다. 모든 Case에서 Rising Duct 출구 체적 유량의 오차율은 약 0.004% 이하로 나타났으며, 해석 결과가 동일한 조건에서 비교되었다고 판단된다.

Table 4.

Probe outlet pressure conditions and rising duct outlet flow rate

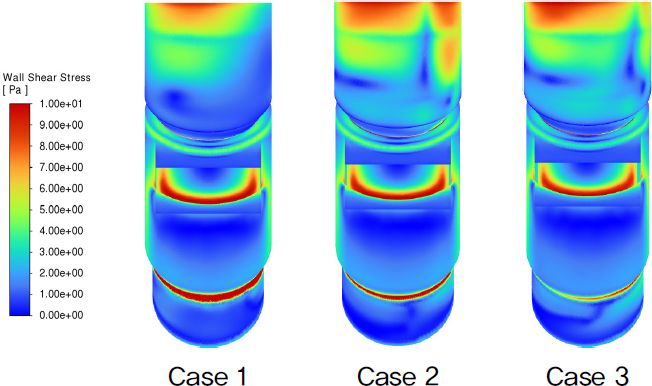
내관과 외관 사이의 단면적이 가장 크게 설계된 Case 1, 2, 3의 프로브 출구 압력 조건을 비교한 결과, Case 1에서의 압력 손실이 가장 적게 나타났다. 이는 동일한 체적 유량 조건에서 내관 단면적의 증가로 인해 유속이 감소하여 압력 손실이 감소한 결과로 해석된다. 그러나 Case 2보다 Case 3에서 압력 손실이 더 적게 나타났으며, 이와 같은 양상은 내관과 외관 사이의 단면적 크기와 관계없이 다른 Case에서도 동일하게 관찰되었다. 프로브 내관의 내경이 1114.86 mm로 설계된 Case에서의 압력 손실은 프로브 엘보 부근에서 발생하는 국부적인 난류 변화로 인해 증가한 것으로 판단되며, 이를 나타내기 위해 Case 1, 2, 3의 엘보 부근 벽면에서의 전단 응력 분포를 비교한 결과를 Fig. 2에 제시하였다. 이러한 결과는 관의 단면적이 증가할수록 유속 감소로 인해 관 내 마찰에 의한 압력 손실은 감소할 수 있으나, 단면적 크기, 설비 구조 및 복합적인 유동 현상에 따라 압력 손실에 미치는 영향이 다르게 나타날 수 있음을 시사한다.^[21] Case 4, 5, 6의 프로브 출구 압력 조건은 Case 1, 2, 3과 유사한 경향을 보였으며, 내관과 외관 사이의 단면적 축소로 인해 냉각 공기 토출 속도가 증가하면서 압력 손실이 다소 증가한 것으로 나타났다. 그러나 내관과 외관 사이의 단면적이 가장 작게 설계된 Case 7, 8, 9에서 가장 낮은 압력 손실을 나타냈다. Case 7, 8, 9는 가스 체류 시간이 이전 Case 대비 0,01 s 단축되었으며, 12% 바이패스 조건을 충족하기 위해 이중관 길이가 짧게 설계되었다. 압력 손실은 이중관의 길이에 비례하여 감소하였으며, 이는 관 내 유속 감소보다 이중관 길이 축소가 압력 손실 감소에 더 효과적임을 시사한다.^[22] 따라서 압력 손실을 최소화하기 위해서는 내관의 단면적을 크게 설계하고 냉각 공기 토출구 간격을 적절히 조정하여 가스 체류 시간을 단축한 구조가 효율적임을 보여준다.

Fig. 2.

Wall shear stress of Case 1, 2, 3

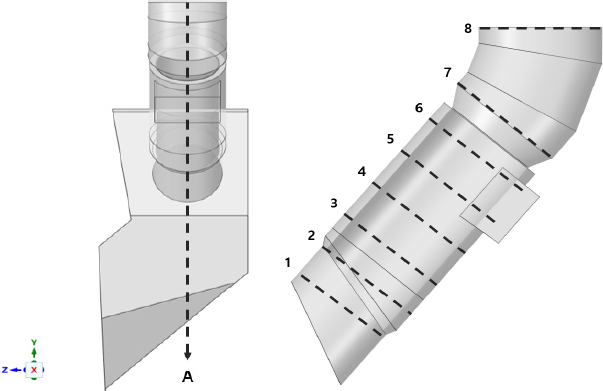
Fig. 3은 해석 결과 후처리를 위한 단면을 나타낸 도식이다. XY 평면에서의 A 단면은 프로브의 중앙부를 기준으로 정의되었으며, 추기 가스 고온 영역 중앙의 냉각 정도를 평가하기 위해 설정되었다. 또한, 1~7 단면은 프로브 내부에서 추기 가스와 냉각 공기가 혼합되는 영역의 유동 특성을 정밀하게 분석하기 위해 정의되었으며, 8 단면은 프로브 출구에서 추기 가스가 냉각되어 배출되는 최종 온도를 평가하기 위해 설정되었다.

Fig. 3.

Post-processing plane

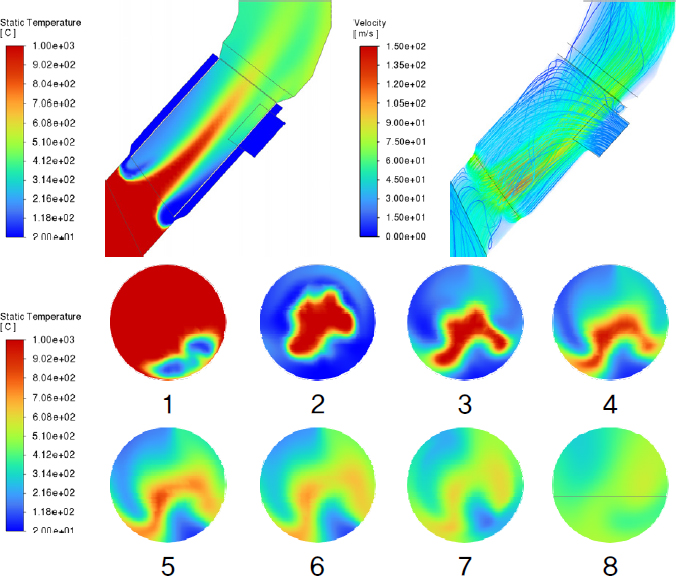
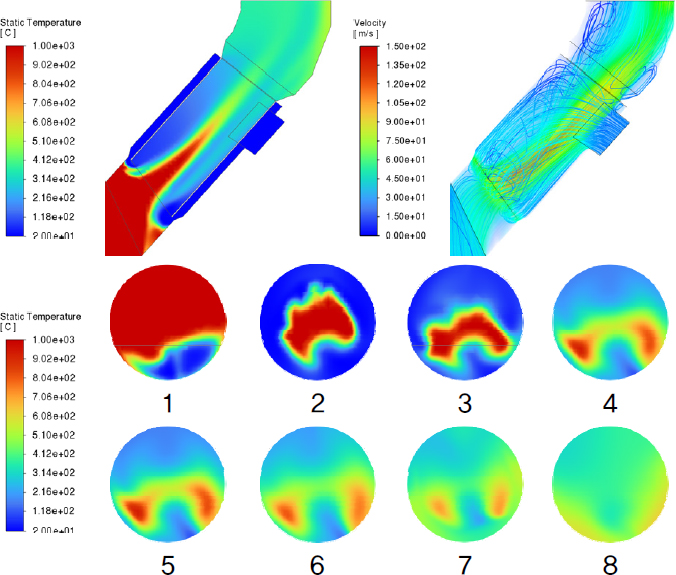
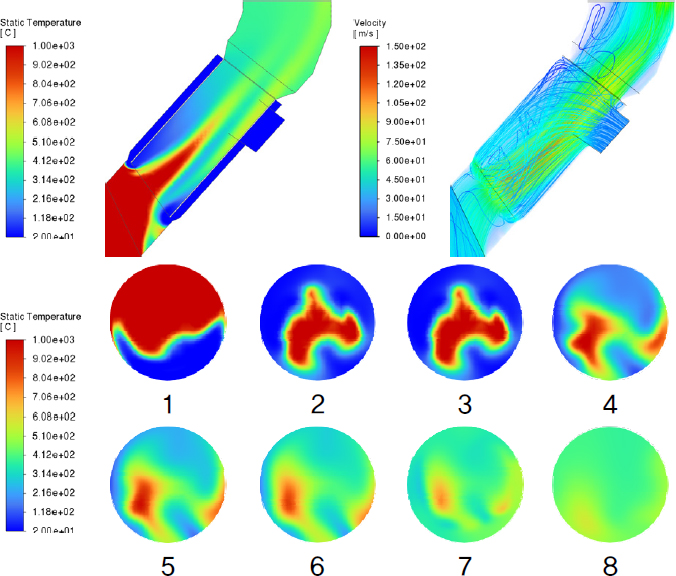
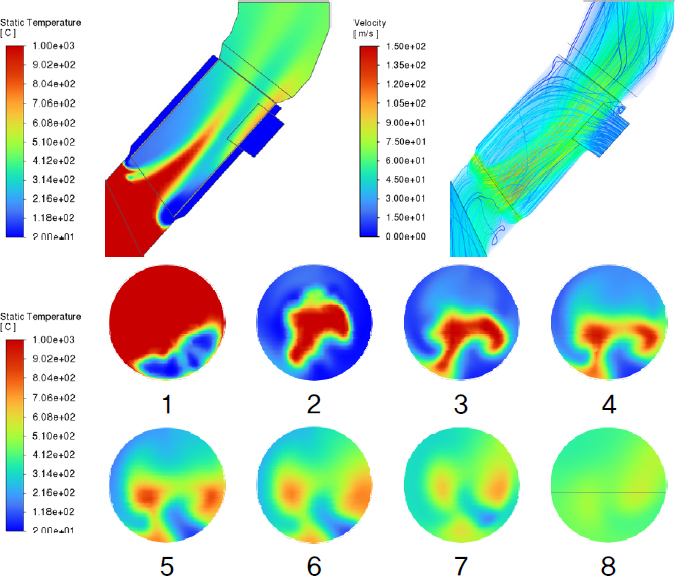
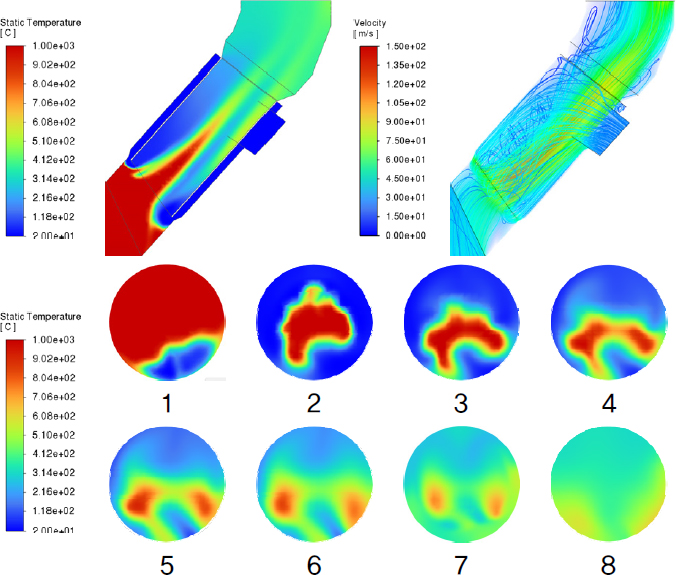
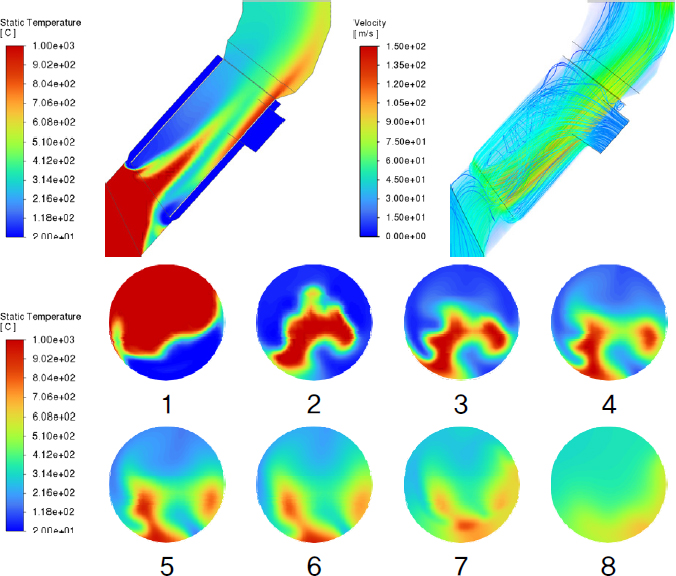
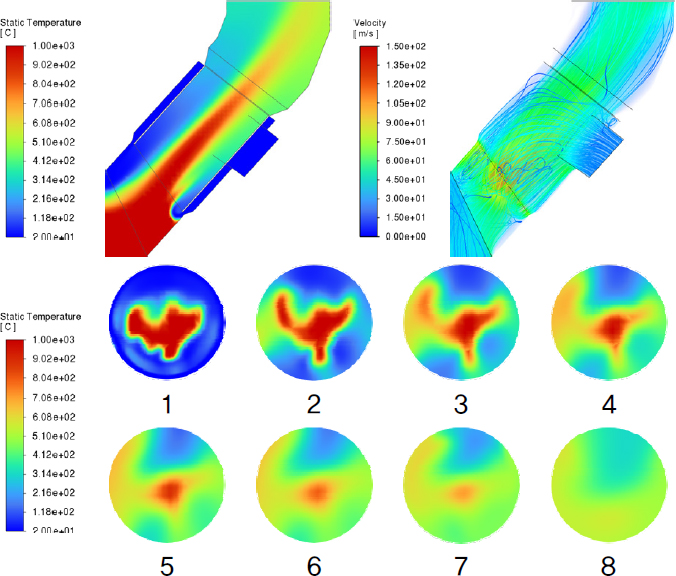
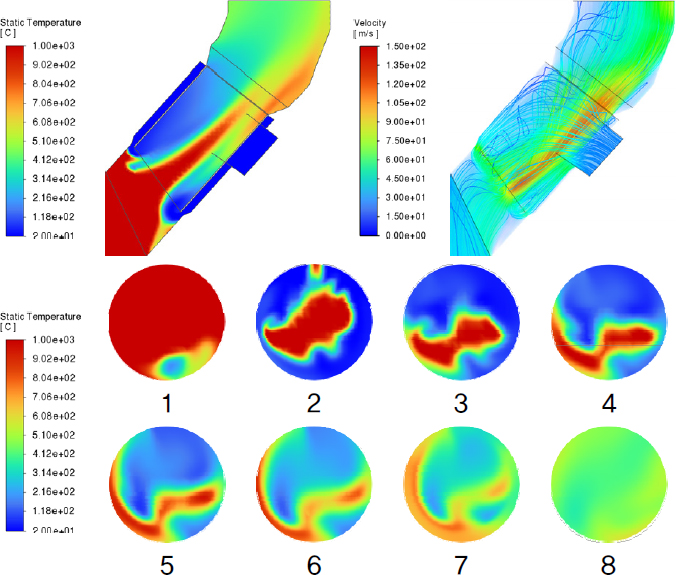
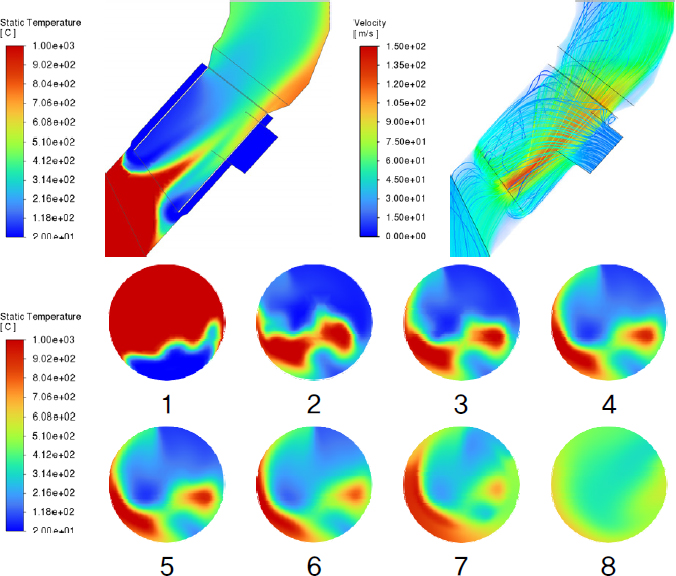
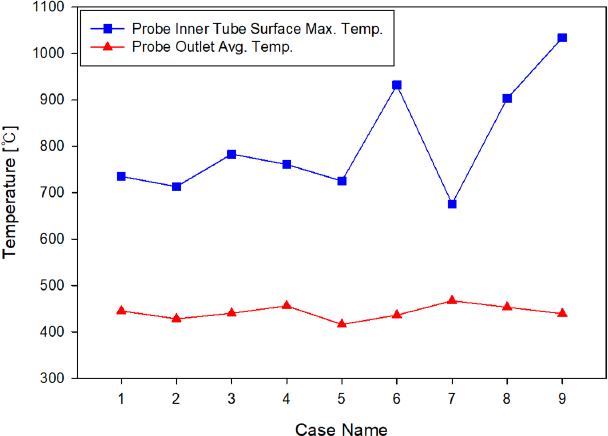
프로브 구조는 냉각 효율 및 시스템 안정성을 향상시키기 위해 추기 가스와 냉각 공기의 혼합을 개선하는 동시에, 설비가 고온 가스에 장시간 노출되지 않도록 설계되어야 한다. 또한, 냉각 공기의 Rising Duct 역류로 인해 코팅 형성이 촉진되는 현상을 방지하기 위한 설계적 고려도 필수적이다. 이에 따라 본 연구에서는 각 Case의 추기 가스와 냉각 공기의 혼합 정도, 설비 표면의 최대 온도, 냉각 공기 역류 여부 등을 종합적으로 분석하여 프로브의 냉각 성능을 최적화하는 것을 목표로 한다. Fig. 4~12는 각 Case에 대한 A 단면 및 1~8 단면의 온도 분포와 프로브 내부의 속도 분포를 나타낸 결과이다. 온도 분포는 contour 기법을 활용하여 나타냈으며, 속도 분포는 volume rendering 및 streamline 기법을 적용하여 시각화하였다. Fig. 13은 프로브 내관 표면에서의 최대 온도 및 출구에서의 평균 온도를 정리한 그래프이다.

Fig. 4.

Temperature and velocity graphic of Case 1

Fig. 5.

Temperature and velocity graphic of Case 2

Fig. 6.

Temperature and velocity graphic of Case 3

Fig. 7.

Temperature and velocity graphic of Case 4

Fig. 8.

Temperature and velocity graphic of Case 5

Fig. 9.

Temperature and velocity graphic of Case 6

Fig. 10.

Temperature and velocity graphic of Case 7

Fig. 11.

Temperature and velocity graphic of Case 8

Fig. 12.

Temperature and velocity graphic of Case 9

Fig. 13.

Graph of probe temperature variation by case

Case 1, 2, 3의 A 단면 온도 분포를 분석한 결과, Case 1에서는 추기 가스의 고온 영역이 프로브 엘보 부근까지 유지된 상태로 배출되는 반면, Case 2와 Case 3에서는 고온 영역이 상대적으로 빠르게 해소되는 것으로 나타났다. 이는 Case 1에서 관 내 유속이 낮아 추기 가스와 냉각 공기의 혼합이 제한적으로 이루어진 데 기인한 것으로 해석되며, Case 2와 Case 3에서는 내관 단면적 축소로 인해 유속이 증가하면서 혼합이 더욱 활발하게 이루어진 것으로 판단된다. 그러나 Case 3에서는 유속 증가로 인한 항력 및 중력의 영향으로 추기 가스의 고온 영역이 프로브 하단 벽면으로 편향되는 현상이 나타났으며,^[23] 이에 따라 내관 표면에서의 최대 온도가 약 783°C로 측정되었다. 이는 Case 1과 Case 2에 비해 다소 높은 수치로, Case 3의 4, 5 단면 온도 분포를 통해 고온 영역이 내관과 접촉하는 면적이 넓어졌음을 확인할 수 있다. 따라서 냉각 공기 토출구 간격이 동일할 경우 내관 단면적이 작을수록 혼합 정도가 개선될 수 있으나, 고온의 가스가 설비 표면과 접촉할 가능성이 높아져 설비의 내구성에 부정적인 영향을 미칠 것으로 예측된다.

Case 4, 5, 6의 해석 결과, 내관과 외관 사이의 단면적 감소로 인해 냉각 공기 토출 속도가 증가하면서 관 내부 고속 영역이 확장되는 양상이 나타났다. 이에 따른 온도 분포의 변동이 확인되었으며, 내관 표면에서의 최대 온도가 Case 1, 2, 3과 비교하여 다소 높게 측정되었다. 특히, Case 6에서는 냉각 공기 토출 속도의 증가 및 내관 단면적 축소로 인해 추기 가스의 고온 영역이 프로브 하단 벽면 쪽으로 편향되는 현상이 두드러지게 나타났으며, 내관 표면에서의 최대 온도는 약 932°C로 측정되었다. 이는 Case 3에 비해 약 150°C 높은 값으로, 냉각 공기 토출구의 간격이 내부 유동장에 미치는 영향이 내관 단면적의 크기보다 더 크게 작용함을 시사한다.

Case 7, 8, 9는 이전 Case들과 비교하여 유동 특성 및 온도 분포에서 뚜렷한 차이를 보였다. Case 7의 경우 내관 표면에서의 최대 온도가 가장 낮게 측정되었으나, A 단면에서 확인된 바와 같이 Rising Duct로 냉각 공기가 역류하는 현상이 발생하였다. 이는 단면적 축소로 인한 압력 불균형, 추기 가스와 냉각 공기 간의 상대적 유속 차이 등 복합적인 요인으로 인해 발생한 것으로 판단된다. Case 8과 Case 9에서는 내관 표면에서의 최대 온도가 각각 903°C와 1,034°C로 나타났으며, 고온의 추기 가스가 냉각되지 않은 상태로 내관 표면에 직접 접촉하는 현상이 관찰되었다. 이에 따라 가스 체류 시간 단축 및 관 내 유속 증가를 유도하는 구조가 과도하게 설계될 경우, 냉각 효율 저하뿐만 아니라 프로브 설비의 내구성 약화도 초래할 것으로 사료된다.

4. 결 론

본 연구는 시멘트 제조 공정에서 연료 대체율 65% 이상 증대 시 바이패스율 12%를 충족하는 프로브의 이중관 구조를 최적화하기 위한 CFD 분석을 수행하였다. 내관 내경, 냉각 공기 토출구 간격, 가스 체류 시간을 설계 변수로 지정하여 내부 가스 흐름 및 열전달 등에 미치는 영향을 파악하기 위해 아홉 가지의 설계 Case를 비교 분석하였으며, 결론은 다음과 같다.

내관 단면적이 증가할수록 관 내 유속이 감소하여 압력 손실이 감소하는 경향을 보였으나, 국부적인 난류 변화 및 설비 구조적 요인에 따라 압력 손실이 증가하는 양상이 나타났다. Case 1, 2, 3과 비교하여 Case 4, 5, 6에서는 냉각 공기 토출구 간격이 감소하여 압력 손실이 다소 증가하였으나, 냉각 공기 토출구 간격이 가장 좁게 설계된 Case 7, 8, 9에서는 가스 체류 시간 단축으로 인해 이중관 길이가 짧게 설계되어 압력 손실이 가장 적게 나타났다. 이에 따라 관 내 유동 특성을 분석하여 적절한 단면적 크기와 설계 조건을 적용하는 것이 중요하며, 압력 손실 측면에서는 내관 단면적을 크게 설계하고 냉각 공기 토출구 간격을 적절히 조정하여 가스 체류 시간이 단축된 설계가 효율적임을 확인하였다.

추기 가스와 냉각 공기의 혼합은 관 내 유속이 증가함에 따라 난류가 활성화되어 개선될 수 있으나, 추기 가스의 고온 영역이 설비 벽면으로 편향되어 설비의 내구성 저하를 초래할 것으로 확인되었다. 또한, 냉각 공기 토출구 간격 및 이중관 길이가 과도하게 최소화될 경우 압력 손실 감소에는 유리하지만, 냉각 공기의 역류 현상이 발생할 가능성이 있어 충분한 가스 체류 시간을 확보하는 것이 중요하다고 판단된다. 이러한 결과는 내관 단면적과 냉각 공기 토출구 간격의 균형 있는 설계가 냉각 효율 및 설비 내구성을 최적화하는 핵심 설계 변수로 작용함을 시사한다.

따라서 본 연구 결과를 종합적으로 고려할 때, 프로브의 운전 비용을 최소화하여 추기 가스를 경제적으로 처리하기 위한 이중관의 구조는 Case 1이 가장 적합한 설계라고 판단된다.

Nomenclature


ρ :	density, kg/m³
t :	time, s
v :	velocity, m/s
∇ :	partial derivative of a quantity
p :	static pressure, N/m³
$τ - ¯$ :	stress tensor, N/m³
$ρ g →$ :	gravitational body force, N/m³
$F →$ :	external body force, N/m³
h :	enthalpy, J/kg
k_eff :	effective conductivity, W/m·K
T :	temperature, K
$J j →$ :	diffusion flux of species j, mol/m²·s
S_h :	volumetric heat source, W/m³
$u i' u j'$ :	fluctuating velocity components, m/s
x_i, x_j :	spatial coordinate, m
μ :	dynamic viscosity coefficient, kg/m·s
G_k :	turbulent kinetic energy due to the mean velocity gradient
G_b :	turbulent kinetic energy due to buoyancy
Y_M :	contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate
C_1ϵ, C_2ϵ, C_3ϵ :	constants
σ_k, σ_ϵ :	turbulent Prandtl numbers
S_m, S_k, S_ϵ :	user-defined source terms
RANS :	raynolds-averaged navier-stokes
SIMPLEC :	semi-implicit method for pressure-linked equation consistent

Acknowledgments

본 연구는 2023년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원(‘RS-2023-00261230’)과 환경부의 폐자원에너지화 전문인력 양성사업 지원으로 수행되었습니다.

References

Presidential Commission on Carbon Neutrality and Green Growth, 2022, “Academic compendium on carbon neutrality (Integrated edition)”, https://www.2050cnc.go.kr/storage/toast/20220906/content/index.html, .
Joint Effort by Relevant Ministries, 2023, “National strategy for carbon neutrality and green growth and the first basic national plan (Medium- and long-term greenhouse gas reduction targets included)”, Presidential Commission on Carbon Neutrality and Green Growth, https://www.2050cnc.go.kr/download/BOARD_ATTACH?storageNo=2403, .
EG-TIPS, 2021, “Enhanced plan for the 2030 nationally determined contribution(NDC)”, https://tips.energy.or.kr/uplolad/carbon/%EC%B2%A8%EB%B6%802_2030%20%EA%B5%AD%EA%B0%80%20%EC%98%A8%EC%8B %A4%EA%B0%80%EC%8A%A4%20%EA%B0%90%EC%B6%95%EB%AA%A9%ED%91%9C(NDC)%20 %EC%83%81%ED%96%A5%EC%95%88-%EC%B5%9C%EC%A2%85.pdf, .
Benhelal, E., Shamsaei, E., and Rashid, M.I., 2021, “Challenges against CO₂ abatement strategies in cement industry: A review”, J. Environ. Sci., 104, 84-101. [https://doi.org/10.1016/j.jes.2020.11.020]
Jo, J.H., Yun, S.I., Lee, S.J., Choi, J.H., and Kim, E.C., 2024, “Study on the utilization of waste plastic in the Korea cement industry and the revision of KS standards for increasing fuel substitution rates”, J Rec Const Resources, 12(3), 306-313.
Jons, E., Hundebol, S., and Clausen, K., 2008, “New reasons for installing a chloride by-pass. Interaction between chloride and sulphur”, 2008 IEEE Cement Industry Technical Conference Record, 195-209. [https://doi.org/10.1109/CITCON.2008.23]
Pieper, C., Wirtz, S., Schaefer, S., and Scherer, V., 2021, “Numerical investigation of the impact of coating layers on RDF combustion and clinker properties in rotary cement kilns”, Fuel, 283, 118951. [https://doi.org/10.1016/j.fuel.2020.118951]
Wojtacha-Rychter, K., Król, M., Gołaszewska, M., Całus-Moszko, J., Małgdziarczyk, M., and Smoliński, A., 2021, “Dust from chlorine bypass installation as cementitious materials replacement in concrete making”, J. Build. Eng., 51, 104309. [https://doi.org/10.1016/j.jobe.2022.104309]
ERA tech, “Recirculation of metals in cement kilns”, http://www.eratech.com/papers/pdf/volatility.pdf, .
Sutou, K., Harada, H., and Ueno, N., 1999, “Chlorine bypass system for stable kiln operation and the recycling of waste”, 1999 IEEE/-IAS/PCA Cement Industry Technical Conference. Conference Record (Cat. No. 99CH36335), 179-193. [https://doi.org/10.1109/CITCON.1999.767038]
Wang, J., Zeng, P., Liu, Z., and Li, Y., 2023, “Manufacture of potassium chloride from cement kiln bypass dust: An industrial implementation case for transforming waste into valuable resources”, Heliyon, 9(11). [https://doi.org/10.1016/j.heliyon.2023.e21806]
Lee, S.H., 2001, “Waste treatment by cement plant-chlorine bypass facility”, Cement, 155, 37-43.
Presidential Commission on Carbon Neutrality and Green Growth, 2021, “2050 Carbon neutrality scenario”, https://www.2050cnc.go.kr/download/BOARD_ATTACH?storageNo=360, .
Jeon, J.M., Hwang, H.J., Kim, C.S., Kwon, W.T., and Oh, S.C., 2024, “Study on the behavior of chlorine in cement kilns for increasing alternative fuel usage and the effect of applying chlorine bypass facilities”, Recources Recycling, 33(6), 15-24. [https://doi.org/10.7844/kirr.2024.33.6.15]
Chen, X., Liu, J., Pang, Y., Chen, J., Chi, L., and Gong, C., 2020, “Developing a new mesh quality evaluation method based on convolutional neural network”, Eng. Appl. Comput. Fluid Mech., 14(1), 391-400. [https://doi.org/10.1080/19942060.2020.1720820]
Kovacevic, A., 2005, “Boundary adaptation in grid generation for CFD analysis of screw compressors”, International Journal for Numerical Methods in Engineering, 64(3), 401-426. [https://doi.org/10.1002/nme.1376]
Ansys, “Fluent theory guide”, Accessed 9 January 2025, https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v241/ko/flu_th/flu_th.html, .
Heo, S.J., Yoh, K.Y., Moon, S.I., and Kim, J.K., 2023, “Analysis of fluid flow characteristics of circular water tank with double panel wall using CFD”, J of Korean Soc Steel Construction, 35(4), 219-227. [https://doi.org/10.7781/kjoss.2023.35.4.219]
Versteeg, H.K., 2007, “An introduction to computational fluid dynamics the finite volume method”, 2nd ed., Pearson Education, India.
Tao, H.-G., Chen, H.-X., Xie, J.-L., and Hu, Y.-P., 2012, “An alternative approach to quantifying fluid flow uniformity based on area-weighted average velocity and mass-weighted average velocity”, Energy and buildings, 45, 116-123. [https://doi.org/10.1016/j.enbuild.2011.10.056]
Hamad, F.A., Faraji, F., Santim, C.G.S., Basha, N., and Ali, Z., 2017, “Investigation of pressure drop in horizontal pipes with different diameters”, Int. J. Multiph. Flow, 91, 120-129. [https://doi.org/10.1016/j.ijmultiphaseflow.2017.01.007]
Adeosun, T.A., Olatunde, O.A., Aderohunmu, J.O., and Ogunjare, T.O., 2009, “Development of unsteady-state Weymouth equations for gas volumetric flow rate in horizontal and inclined pipes”, J. Nat. Gas Eng., 1(4-5), 113-117. [https://doi.org/10.1016/j.jngse.2009.09.001]
Wang, K., Li, X., Wang, Y., and He, R., 2017, “Numerical investigation of the erosion behavior in elbows of petroleum pipelines”, Powder Technol., 314, 490-499. [https://doi.org/10.1016/j.powtec.2016.12.083]

Case	Inner Tube		Outer Tube	Double-Tube Length
Case	Inner Diameter	Outer Diameter	Inner Diameter	Double-Tube Length
1	1143.33 mm	1171.33 mm	1420.21 mm	1910 mm
2	1114.86 mm	1142.86 mm	1396.83 mm	2010 mm
3	1087.65 mm	1115.65 mm	1374.65 mm	2120 mm
4	1143.33 mm	1171.33 mm	1397.27 mm	1910 mm
5	1114.86 mm	1142.86 mm	1373.50 mm	2010 mm
6	1087.65 mm	1115.65 mm	1350.93 mm	2120 mm
7	1143.33 mm	1171.33 mm	1378.28 mm	1280 mm
8	1114.86 mm	1142.86 mm	1354.17 mm	1340 mm
9	1087.65 mm	1115.65 mm	1331.28 mm	1410 mm

Case	Cells	Skewness	Orthogonal
1	3,284,492	0.59	0.30
2	3,343,572	0.51
3	3,396,277	0.55
4	3,228,919	0.56
5	2,032,717	0.54
6	3,375,202	0.53
7	2,601,355	0.55
8	2,581,881	0.58
9	2,666,719	0.55

Zone		Conditions
Rising Duct	Inlet	Velocity	27.68 m/s
		Temperature	1,200°C
		Species Mass Fractions	O₂	0.017
			H₂0	0.065
			CO₂	0.174
			N₂	0.744
	Outlet	Gauge Pressure	-513.97 Pa
Probe	Inlet	Velocity	18.39 m/s
		Temperature	20°C
		Species Mass Fractions	Air	1
	Outlet	Gauge Pressure	-
Operating Pressure			98751.2 Pa

Case	Probe Outlet Pressure	Rising Duct Outlet Volume Flow Rate
1	-2,699 Pa	53.5637 Nm³/s
2	-2,854 Pa	53.5651 Nm³/s
3	-2,800 Pa	53.5651 Nm³/s
4	-2,783 Pa	53.5646 Nm³/s
5	-2,906 Pa	53.5656 Nm³/s
6	-2,820 Pa	53.5633 Nm³/s
7	-2,560 Pa	53.5649 Nm³/s
8	-2,844 Pa	53.5642 Nm³/s
9	-2,740 Pa	53.5651 Nm³/s