와류기인진동을 이용한 신재생에너지 발전에서 유체력 추정연구


Copyright © 2023 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Vortex-induced vibrations are a type of flow-induced vibrations caused by alternating lift forces. With increasing demand for renewable energy, the application of vortex-induced vibrations to renewable energy has been widely studied. Vortex-induced vibrations for aquatic clean energy (VIVACE) converter is a renewable energy device that generates electricity from rivers or oceans using vortex-induced vibrations. To increase the design life and power harnessing capacity of the VIVACE converter, the estimation of fluid forces due to vortex-induced vibrations is essential. Herein, vortex-induced vibrations were experimentally tested, and their amplitude and frequency response were measured. The amplitude results showed four different branches: initial branch, upper branch, lower branch, and desynchronization range. According to the fluid force coefficient results, the maximum lift coefficient occurred at the upper branch. Additionally, a mathematical model is proposed to estimate fluid forces due to vortex-induced vibrations without using measurement devices. This mathematical model enables the estimation of fluid force coefficients and phase lag using amplitude and frequency response of vortex-induced vibrations.
Keywords:
Flow-induced vibrations, Vortex-induced vibrations, Current energy, Fluid force키워드:
유동기인진동, 와류기인진동, 조력에너지, 유체력1. 서 론
와류기인진동 혹은 와류유발진동(Vortex-induced vibrations)은 유동기인진동(Flow-induced vibrations)의 한 종류이며 주로 원형 구조물에서 발생한다.[1] 와류기인진동은 원형 구조물이 유동에 노출될 때, 원형 구조물에서 발생한 와류(vortex)가 원형 구조물의 뒤편에서 떨어져 나가면서 원형 구조물에 양력(Lift force)을 발생시키며, 결과적으로 구조물의 진동을 발생시키는 현상을 의미한다. 최근에 신재생에너지에 대한 수요가 늘어남에 따라서, 태양열, 풍력, 파력 외에 다른 에너지원으로 유동기인진동을 이용한 신재생에너지 발전 연구가 각광을 받고 있으며 전세계적으로 활발히 연구가 되고있다.[2~5] 특히, 미국 미시건 대학교(University of Michigan)의 해양신재생에너지 연구실(Marine Renewable Energy Laboratory)에서는 와류기인진동을 이용해서 강이나 바다에서 전기적 에너지를 만들 수 있는 VIVACE(Vortex Induced Vibrations for Aquatic Clean Energy) 장치를 개발하였다.[6] Fig. 1은 VIVACE 장치의 개념도를 보여준다. VIVACE 장치는 여러 개의 원통형 실린더로 구성되어 있으며, 조류가 원통형 실린더를 흘러 지나감에 따라서, 원통형 실린더 뒤편에서 발생한 와류가 실린더에서 떨어져 나가면서 원통형 실린더를 아래 위로 움직이게 하는 진동을 발생시킨다.
실해역에서 VIVACE 장치의 안전한 운영과 정확한 에너지 발전량 계산을 위해, 와류기인진동이 구조물에 가하는 유체력(Fluid force)을 산정해야 한다. 그러나, 와류기인진동은 구조물의 강성, 감쇠비, 질량 등 시스템의 특성에 많은 영향을 받는다. 또한, 와류기인진동의 비선형적 특성으로 인해서 정확한 유체력을 추정하기가 어렵다.[7] 최근에 전산유체역학(Computational Fluid Dynamics: CFD)이나 유체구조 상호작용(Fluid-Structure Interaction: FSI) 해석 소프트웨어가 발달함에 따라서, 수치해석적으로 유체력 추정이 가능하나, 정확한 수치해석을 위해서는 여전히 실험 데이터가 필요하다. 특히, 정확한 유체력을 측정하기 위해서는 로드셀(load cell)이나 센서처럼 측정장치가 필요하다. 이러한 장치들을 구비하기가 쉽지 않기 때문에, 이 논문에서는 실험을 통해서 계측한 와류기인진동의 진폭과 진동수를 이용해서 와류기인진동에 의해 발생한 유체력을 추정하는 방법을 연구했다. 이를 위해서 구조물의 운동방정식으로부터 수학적 모델이 유도되었다.
섹션2에서는 유동기인진동 실험방법 및 실험시설을 소개하였다. 섹션3에서는 실험을 통해서 측정한 와류기인진동의 진폭과 진동수 반응이 제시되었다. 또한, 와류기인진동 특징을 정확히 분석하기 위해서, 시계열에 따른 진폭 반응도 함께 보여주었다. 특히, 와류기인진동의 유체력을 측정장비 없이 추정하기 위해서, 와류기인진동이 발생하는 구조물의 운동방정식으로부터 수학적 모델을 유도하였다.
2. 실험 방법
이 섹션에서는 와류기인진동을 실험하기 위한 실험 장치와 진동장치를 설명한다.
2.1 회류수조
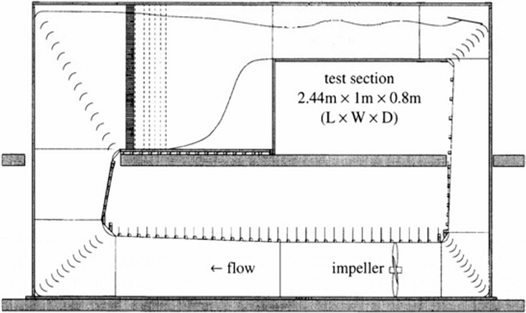
실험은 미국 미시건 대학교(University of Michigan)의 회류 수조에서 행해졌다. Fig. 2는 회류 수조의 개략도를 보여준다. Fig. 2에 나타난 것처럼, 회류 수조는 2층으로 이루어져 있으며 1층에는 20 HP(Horse Power) 을 가진 모터가 설치되어 있다. 모터에는 임펠러(impeller)가 달려있으며, 모터를 구동시켜 물을 수조안에서 회류 시키도록 설계 되어있다. 2층에 위치한 테스트 섹션(test section)의 치수는 2.44 m × 1 m × 0.8 m(L × W × D)이며, 테스트 섹션에서 물은 일정한 유속으로 흐르도록 설계되었다. 회류 수조의 최대 유속은 1.6 m/s이며, 자유표면(free surface)에서의 난류강도(turbulence intensity)는 0.1% 보다 낮도록 설계되었다.[8]
2.2 진동장치
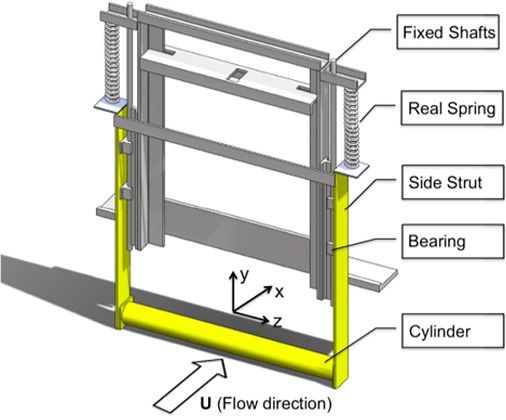
진동 장치에서 와류기인진동을 발생시키기 위해서 표면이 매끄러운 원통형 실린더가 구조물로 선택되었다. 원통형 실린더의 직경(D)과 길이(L)는 각각 0.0889 m 와 0.914 m이다. Fig. 3에 나타난 것처럼, 원통형 실린더는 양 끝에 달린 스프링에 의해서 지지되어 있다. 유체가 원통형 실린더를 지나가면, 와류기인진동에 의해서 발생한 양력이 원통형 실린더를 유체의 흐름에 수직방향으로 움직이도록 설계하었다. 실험에 사용된 스프링은 선형 스프링으로 스프링 계수(k)는 763 N/m이며 감쇠계수(c)는 3.44 Ns/m이다. 장치의 스프링 계수와 감쇠 계수는 자유 감쇠실험(free decay test)을 통해서 측정되었다. 선형 스프링도 스프링의 변위가 커지면 비선형적 특성을 가진다. 본 실험에서 사용된 유동기인진동의 경우, 최대 진폭이 제한되는 특징을 가지고 있기 때문에 스프링은 선형 범위안에서 작동하였다. 또한, 실험의 오차를 줄이기 위해서 실험과정 동안 과도한 진폭이 발생하는지에 대해서 관측을 하였다. 본 실험에서 감쇠기의 모델로 점성감쇠가 사용되었다. 점성감쇠 모델은 물리적 현상을 잘 묘사하며, 특히 운동방정식의 수학적 용이성으로 인해 많은 진동시스템에서 사용되고 있다. 따라서, 이번 연구에서도 점성감쇠가 사용되었다. 실험에 사용된 진동 장치의 시스템 특성은 Table 1에 요약 되어있다.
원통형 실린더의 움직임은 선형 위치 변환기(linear position transducer)를 통해서 실시간으로 계측되었다. 실험에서 원통형 실린더의 움직임은 고정된 유속에서 60초 동안 기록되었으며, 데이터의 샘플링 주파수(sampling frequency)는 100 Hz였다. 유속을 0.45 m/s부터 1.25 m/s까지 일정한 간격으로 증가시키면서, 실린더의 움직임을 기록하였다. 유속을 증가시킬 경우, 유속이 일정할 때까지 기다린 후, 실린더의 움직임을 측정하였으며, 실린더 진폭은 실린더의 움직임을 60초 동안 기록한 양의 진폭과 음의 진폭 중에서, 가장 큰 진폭 60개를 RMS(Root Mean Square) 방법을 이용해서 산출했다. 실린더의 움직임 진동수의 경우, 60초 동안 측정된 시계열 데이터를 PSD(Power Spectrum Density) 변환을 해서 계산하였다. 특히, lower branch 처럼 여러 개의 peak 값이 나타나는 경우, 최대 값을 실린더의 움직임 진동수로 사용하였다.
3. 실험 결과
이 섹션에서는 와류기인진동 실험 결과와 와류기인진동의 유체력을 계산하기 위한 수학적 모델이 유도되었다. 유도된 수학모델을 이용해서 계산된 와류기인진동의 유체상수 및 위상차 결과가 제시되었다.
3.1 진폭 및 진동수 반응
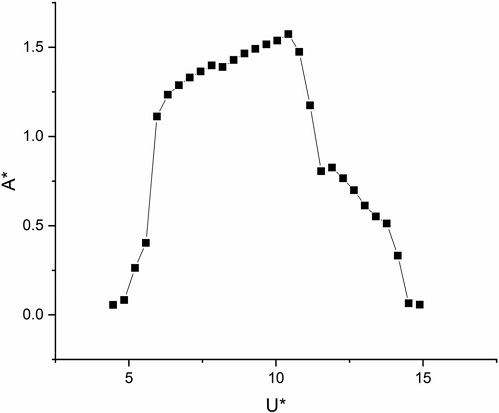
Fig. 4는 유속에 따른 실린더의 진폭을 보여준다. 유속과 실린더의 진폭은 각각 무차원수인 U*와 A*로 변환되어서 표현되었다. U*는 reduced velocity라고 하며 유속을 시스템의 고유진동수와 실린더의 직경을 나눈 값으로 정의된다. 이번 연구에서는 시스템의 고유진동수 와 실린더의 직경이 고정되어 있기 때문에 U*는 유속의 증가에 따라서 선형적으로 증가한다.
와류기인진동은 실린더에서 와류가 떨어지는 진동수(vortex shedding frequency)와 시스템의 고유진동수(natural frequency)가 같아질 때 발생하는 공진 현상이나, 선형 진동기(linear oscillator)의 공진에 비해서 넓은 유속에 대해서 큰 진폭이 발생하며, 또한 비선형적인 특성도 가지고 있다. Fig. 4에 나타난 것처럼, 실린더의 진폭은 U* 따라서 크게 다음과 같이 4개의 영역으로 나눌 수 있다. 4<U*<5.5 구간은 initial branch라고 하며, 이 영역은 실린더에서 와류가 떨어지는 진동수와 시스템의 고유진동수가 같아지기 전을 의미한다. 즉, 와류기인진동이 발생하고 큰 진폭이 발생하기전의 영역을 의미한다. 5.5<U*<10.8 구간은 upper branch라고 하며 와류기인진동에서 진폭이 가장 큰 영역을 의미하며, 큰 진폭은 넓은 유속에 걸쳐서 나타난다. Upper branch에서는 실린더의 움직임 진동수와 시스템의 고유진동수가 거의 같으며, 특이하게 이 때 유속을 증가시키더라도 실린더에서 와류가 떨어지는 진동수는 시스템의 고유진동수와 거의 일정한 상태를 유지한다. 이를 락인(locked in) 혹은 동기화(synchronization) 되었다고 말을 한다. 10.8<U*<12.2 구간은 lower branch라고 하며, 실린더에서 와류가 떨어지는 진동수가 고유진동수랑 서서히 벗어나기 시작한다. 따라서, 실린더의 진폭도 upper branch 비해서 많이 낮아진다. 12.2<U* 인 경우, 비동기화(desynchronization) 영역이라고 하며, 실린더에서 와류가 떨어지는 진동수가 고유진동수와 완전히 벗어남에 따라 실린더의 진폭 역시 거의 없어진다.
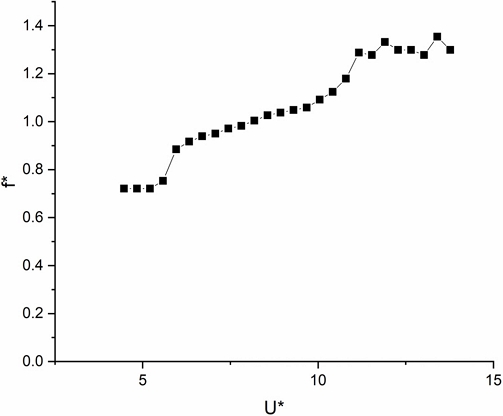
Fig. 5는 유속에 따른 실린더의 움직임 진동수를 나타낸다. 유속과 실린더의 움직임 진동수는 U*와 f*로 변환되어서 표현되었다. f*는 실린더의 움직임 진동수(oscillation frequency)를 시스템의 고유진동수로 나눈 값으로 정의된다. Initial branch에서 f*는 0.6보다 낮은 값을 유지하다가 upper branch에서 실린더의 움직임이 커지면서 1에 가까운 값을 가지게 된다. Reduced velocity가 증가함에 따라서 f*는 서서히 증가하다가 lower branch에서는 f*는 약 1.3 값을 유지한다. 비동기화 영역에서는 실린더의 움직임이 거의 없기 때문에 명확한 실린더의 움직임 주기는 관측되지 않았다.
3.2 시계열 반응
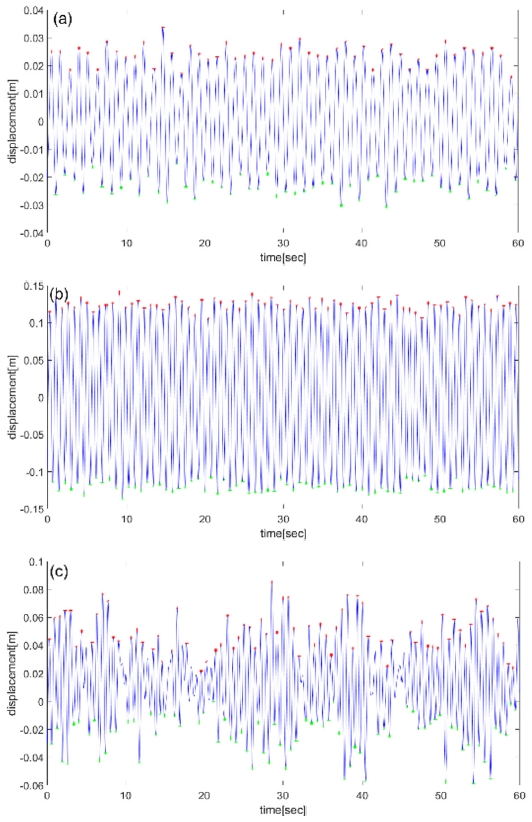
Fig. 6은 각각의 영역에서 시간에 따른 실린더의 진폭반응을 보여준다. Initial branch에서는 상당한 실린더 진폭이 발생하지만 실린더의 반응은 약간 불규칙적인 형태를 띄고 있다. 유속을 증가시켜서 upper branch에 도달하면, 실린더의 반응은 sine 함수처럼 규칙적인 정현응답(sinusoidal response)을 가진다. 유속을 더욱더 증가시켜서 lower branch에 도달하면, initial branch 보다 더 불규칙적인 실린더 응답이 다시 발생한다. 비동기화 영역에서는 실린더에서 와류가 떨어지는 진동수가 시스템의 고유진동수와 완전히 벗어남에 따라서 실린더의 응답은 거의 사라진다. 시계열에 따른 진폭반응으로부터, 각각의 영역에서 와류기인진동의 응답이 어떻게 발생하는지 확인이 가능하다.
3.3 유체력 계산
선형 스프링에 매달린 원통형 실린더의 움직임은 식 (1) 과 같이 질량-감쇠-스프링(mass-dashpot-spring) 운동방정식으로 표현될 수 있다. 식 (1)에서 F는 시간에 따라서 변화는 유체력을 의미하며, 와류기인진동에서 F는 비선형적인 특성을 가지고 있다.
| (1) |
식 (1)에서 실린더의 변위와 유체력에 를 각각 대입한 후, sin 항과 cos 항으로 정리를 하면, 식 (2)를 얻게 된다.
| (2) |
식 (2)를 만족시키기 위해서는 sin 항과 cos 항 앞의 항이 0이어야 하며, 그 결과 식 (3), (4)를 얻게 된다.
| (3) |
| (4) |
무차원 변수를 이용해서 식을 변형시키면, 식 (3), (4)는 식 (5), (6)으로 바뀌게 된다.
| (5) |
| (6) |
식 (5)와 (6)을 사용해서 유체력 계수와 위상차에 대한 식 (7), (8)을 얻게 된다.
| (7) |
| (8) |
식 (7), (8)을 이용하면, 실험에서 측정한 진폭과 진동수를 이용해서 와류기인진동의 유체력계수 및 위상차를 계산할 수 있다. 식 (1)은 Bernitsas et al.(2008)[9] 연구에서 사용된 와류기인진동의 운동방정식과 같은 식이지만, 식의 전개에서 Bernitsas et al.[9]의 연구와 다음과 같은 차이점이 있다. 이전 연구에서는 유체력을 viscos 항목과 inviscid 항목으로 나누어서 식을 전개했지만, 본 연구에서 전체 유체력에 초점을 맞추었기 때문에 viscos 와 inviscid 항목으로 나누지 않았다. 또한, Bernitsas et al.(2008)[9]의 연구에서 inviscid 항목에서 사용한 added mass 값은 ideal fluid에 대한 값인 이 사용되었다. 유속에서 물체의 움직임에 따라서 added mass가 변하기 때문에 어떤 added mass를 쓰는 것이 맞는지는 아직 학계에서 논의가 되고 있다. 따라서, 본 연구에서는 added mass 항목을 유체력에 포함하는 방향으로 식을 전개하였다. Bernitsas et al.(2008)[9]가 유도한 운동방정식에서 유체력을 계산하기 위해서는 inverse 방법이 필요하다. Inverse 방법은 필연적으로 변위를 미분을 해야 되기 때문에, 실험에서 발생한 계측 노이즈가 증폭되는 현상이 발생한다. 이 연구의 목적 중 하나는 inverse 방법을 사용하지 않고, 진폭과 진동수만으로 유체력을 빠르게 추정하기 위한 수학적 식의 유도이기 때문에, Bernitsas et al.(2008)[9] 방법 보다 더 빠르게 유체력을 추정할 수 있다.
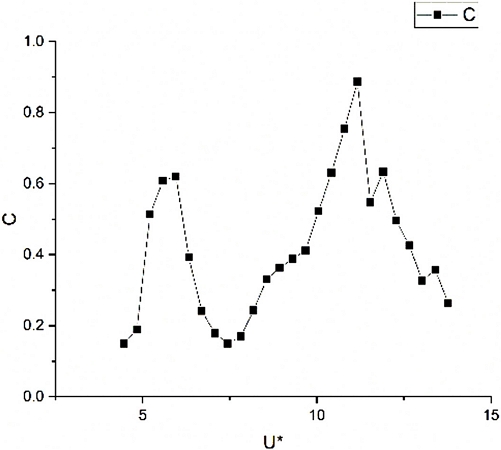
Fig. 7, 8은 섹션 3.1에서 얻어진 데이터를 바탕으로 계산한 유체력계수 및 위상차 결과이다. 유체력계수는 initial branch가 끝나는 지점에서 점프를 한다. Upper branch가 시작되면서 유체력계수는 급격하게 감소하게 된다. 그 후, upper branch영역에서 유체력은 다시 증가하다가 진폭이 가장 크게 발생하는 영역에서 최댓값을 가지게 된다. Lower branch에서는 유체력계수가 점진적으로 감소한다. 위상차의 경우, Initial branch 영역에서 4°-5°의 값을 가진다. Upper branch 영역에서는 위상차가 급격하게 증가를 하며 upper branch 영역의 끝에서는 약 175°가 된다. Lower branch 영역에서는 위상차 변화가 거의 없으며 약 175°의 값을 유지한다. 식 (7), (8)을 이용하면 계측 장비 없이 손쉽게 와류기인진동에 의한 유체력과 위상차를 계산할 수 있다. 그러나, 수학적 모델의 유도과정에서 규칙적인 정현파 응답으로 가정했기 때문에, Upper branch 영역에서 가장 정확도가 높으며, Lower branch 영역에서는 정확도가 떨어질 것으로 예상된다.
4. 결 론
원통형 실린더에 가해지는 와류기인진동의 유체력을 계산하기 위해서, 실험적으로 와류기인진동을 발생시켰다. 실험에서 와류기인진동의 진폭과 진동수를 계측하였으며, 계측된 데이터와 수학적 모델을 이용해서 와류기인진동의 유체력을 추정하였다. 그 결과, 아래와 같은 결론을 이끌어냈다.
- 1) 와류기인진동의 진폭은 reduced velocity에 영향을 받으며, 진폭의 구간은 initial branch, upper branch, lower branch, desynchronization 영역으로 나누어진다.
- 2) 와류기인진동의 진동수는 upper branch 영역에서 거의 1에 가까운 값을 유지하다가 lower branch부터 진동수가 증가해서 1을 벗어나게 된다.
- 3) 와류기인진동의 시계열 반응에서, 와류기인진동은 upper branch, initial branch, lower branch 순으로 규칙적인 정현파 응답을 보인다.
- 4) 와류기인진동의 유체력을 추정하기 위해서 수학적 모델링이 사용되었다. 수학적 모델링은 규칙적인 정현파 응답을 가정했기 때문에, upper branch 영역에서 가장 오차가 적으며, lower branch 영역에서 가장 오차가 크다.
- 5) 유체력계수 계산 결과, 유체력계수는 와류기인진동 영역에 많은 영향을 받았으며, 최댓값은 Upper branch 영역에서 발생했다.
이번 연구의 결과는 다양하게 활용될 수 있으며, 이 연구의 후속으로 아래와 같은 연구를 계획 중이다. 1) 에너지 생산을 위한 harness damping이 추가된 경우에 대한 유체력 추정 연구, 2) 시계열을 이용한 유체력 추정 연구, 3) 유체력을 직접 측정해서 추정치를 비교 검증하는 연구
Nomenclature
| A : | circular cylinder amplitude [m] |
| A*(=A/D) : | dimensionless amplitude [-] |
| c : | system damping coefficient [Ns/m] |
| C : | fluid force coefficient [-] |
| D : | circular cylinder diameter [m] |
| fosc : | oscillating frequency of circular cylinder [Hz] |
| fn,w : | natural frequency of circular cylinder in still water [Hz] |
| f* : | dimensionless frequency [-] |
| F : | fluid force on circular cylinder [N] |
| k : | system stiffness [N/m] |
| L : | circular cylinder length [m] |
| m : | oscillating mass [kg] |
| ma : | added mass [kg] |
| mcylinder : | cylinder mass [kg] |
| m* : | mass ratio [-] |
| U : | flow speed [m/s] |
| U*(=U/(fn,wD) : | reduced velocity [-] |
| S : | reference cylinder area [m2] |
| y : | cylinder displacement [m] |
| : | cylinder velocity [m/s] |
| : | cylinder acceleration [m/s2] |
| ρ : | water density [kg/m3] |
| ζ : | damping ratio [-] |
Acknowledgments
이 연구는 2022년도 계명대학교 비사연구기금으로 이루어졌음(20220231).
References
- Blevins, R.D., 1990, “Flow-induced Vibration”, 2nd ed., Van Nostrand Reinhold, New York.
-
Ma, X., and Zhou, S., 2022, “A review of flow-induced vibration energy harvesters”, Energy Convers. Manag., 254, 115223.
[https://doi.org/10.1016/j.enconman.2022.115223]

-
Wang, J., Geng, L., Ding, L., Zhu, H., and Yurchenko, D., 2020, “The state-of-the-art review on energy harvesting from flow-induced vibrations”, Applied Energy, 267, 114902.
[https://doi.org/10.1016/j.apenergy.2020.114902]

-
Lv, Y., Sun, L., Bernitsas, M. M., and Sun, H., 2021, “A comprehensive review of nonlinear oscillators in hydrokinetic energy harnessing using flow-induced vibrations”, Renewable and Sustainable Energy Rev., 150, 111388.
[https://doi.org/10.1016/j.rser.2021.111388]

-
Kim, E.S., Park, H., Kim, D.H., Baek, H.M., and M.M. Bernitsas, 2020, “Effect of damping ratios of power generators on power efficiency of an ocean renewable energy converter utilizing flow induced vibrations of two circular cylinders”, New. Renew. Energy, 16(1), 31-40.
[https://doi.org/10.7849/ksnre.2020.2043]

-
Kim, E.S., Sun, H., Park, H.R., Shin, S.C., Chae, E.J., Oudekirk, R., and Bernitsas, M.M., 2021, “Development of an alternating lift converter utilizing flow-induced oscillations to harness horizontal hydrokinetic energy”, Renewable and Sustainable Energy Rev., 145, 111094.
[https://doi.org/10.1016/j.rser.2021.111094]

-
Williamson, C. H. K., and Govardhan, R., 2004, “Vortex induced vibrations”, Annual Review Fluid Mechanics, 36, 413-455.
[https://doi.org/10.1146/annurev.fluid.36.050802.122128]

-
Walker, D.T., Lyzenga, D.R., Ericson, E. A., and Lund, D. E., 1996, “Radar backscatter and surface roughness measurements for stationary breaking waves”, Proceedings of the Royal Society Lond. A, 452(1952), 1953-1984.
[https://doi.org/10.1098/rspa.1996.0104]

-
Bernitsas, M.M., Raghavan, K., Ben-Simon, Y., and Garcia, E. M. H., 2008, “VIVACE (Vortex Induced Vibration Aquatic Clean Energy): A new concept in generation of clean and renewable energy from fluid flow”, J. Offshore Mech. Arct. Eng., 130(4), 041101.
[https://doi.org/10.1115/1.2957913]