The Korean Society For New And Renewable Energy

[ Article ]

New & Renewable Energy - Vol. 19, No. 2, pp.1-12

ISSN: 1738-3935 (Print) 2713-9999 (Online)

Article No. [2023-6-HE-001]

Print publication date 25 Jun 2023

Received 17 Jan 2023 Revised 17 Apr 2023 Accepted 20 Apr 2023

DOI: https://doi.org/10.7849/ksnre.2023.0001

촉매유효도 상관식에 기반한 마이크로 채널형 수증기/메탄 개질기의 간략화된 1차원 해석모델의 개발

오윤석¹⁾

; 이대훈²⁾

; 남진현³⁾^{, *}

Development of Simplified One-dimensional Model for Microchannel Steam/Methane Reformers based on Catalyst Effectiveness Factor Correlations

Yun Seok Oh¹⁾

; Dae-Hoon Lee²⁾

; Jin Hyun Nam³⁾^{, *}

1)Ph.D. Candidate, Graduate School of Mechanical Engineering, Seoul National University
2)M.S. Student, Graduate School of Mechanical Engineering, Seoul National University
3)Professor, School of Mechanical Engineering, Daegu University

Correspondence to: * jhnam@daegu.ac.kr Tel: +82-53-850-6675 Fax: +82-53-850-6689

Copyright © 2023 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

In this study, an efficient one-dimensional model was developed for predicting microchannel steam/methane reformers with thin washcoat catalyst layers with a focus on low-pressure reforming conditions suitable for distributed hydrogen production systems for fuel cell applications. The governing equations for steam/methane mixture gas flowing through the microchannel reformer were derived considering the species conservation with reforming reactions and energy conservation with external convective heat supply. The reaction rates for the developed model were simply determined through the catalyst effectiveness factor correlations instead of performing complicated calculations for the steam/methane reforming process occurring inside the washcoat catalyst layers. The accuracy of the developed was verified by comparing the results obtained herein with those obtained by the detailed computational fluid dynamics calculation for the same microchannel reformer.

Keywords:

Hydrogen production, Steam/Methane reforming, Microchannel reformer, One-Dimensional model, Washcoat catalyst layer, Effectiveness factor correlation

키워드:

수소생산, 수증기/메탄 개질, 마이크로채널 개질기, 1차원 모델, 와시코트 촉매층, 촉매유효도 상관식

1. 서 론

화석연료가 환경오염 및 기후변화에 미치는 부정적인 영향으로 인하여 친환경 대체에너지원에 대한 관심과 연구가 증가하고 있다.^[1,2] 수소는 수소엔진이나 연료전지를 이용한 동력생산 시 유해물질의 배출이 거의 없어 친환경적이다. 이론적으로는 물의 분해를 통해 생산할 수 있으므로 공급량에 제한이 없으며 재생 가능한 생산방식을 활용하는 경우 완전한 신재생 에너지원으로 취급될 수 있다. 그러나 현재 상업적으로 이용 가능한 대부분의 수소는 경제성의 이유로 대규모 개질플랜트에서 천연가스의 수증기 개질을 통해 생산된다. 이 공정은 수증기/메탄 개질(SMR, Steam Methane Reforming)이라 지칭하기도 하며 수소를 생산하는 가장 일반적이고 기술적 성숙도가 높은 공정이다.^[3~5]

최근에는 이미 확립되어 있는 도시가스 공급망을 활용하여 현장(On-Site)에서 바로 수소를 생산하여 공급할 수 있는 소규모 수증기/메탄 개질시스템이 많은 관심을 받고 있다. 이러한 분산형 수소생산시스템은 수소의 대량 운송 및 저장과 관련된 위험을 상당 부분 줄일 수 있는 장점이 있다. 특히 고효율 수소연료전지와 결합되어 주거용 및 상업용 분산발전시스템이나 연료전지 차량을 위한 수소충전소 구축 등에 다양한 활용성을 갖추고 있어 관련 연구가 활발하게 진행되고 있다.^[6~8]

일반적으로 수증기/메탄 개질반응은 강한 흡열반응으로 고온의 운전조건에서 메탄이 분해되어 수소가 생성되는 정반응이 우세해진다. 그러나 작동온도는 개질시스템의 수명과 직접적으로 연관되며 온도가 올라감에 따라 핫스팟(Hot Spot) 등 과열위험이 높아지며 그 결과 내열 재료비용도 증가한다. 따라서 경제성과 안전을 고려하면서도 수소 생산량을 증가시키기 위한 수증기/메탄 개질기의 설계 및 운전조건 최적화가 더욱 중요해진다.^[9] 특히 본 연구에서 고려하는 소규모 분산형 수증기/메탄 개질기의 경우, 기존에 잘 정립된 대규모 개질플랜트에서와는 달리, 장치의 소형화에 따른 열효율 감소 등 새로운 공학적 설계 고려사항이 대두되며 따라서 정확한 개질공정의 해석이 더욱 중요해진다.

수증기/메탄 개질공정의 해석은 다공성 촉매층 내부에서 일어나는 열전달, 물질전달, 개질반응에 대한 정확한 계산을 필요로 한다. 이를 위하여 일반적으로 많은 수의 격자가 다공성 촉매층 표면근처 영역에 배치되어야 하며 그 결과 계산시간이 증가하게 된다. 촉매유효도(Catalyst Effectiveness Factor)는 촉매층 표면에서의 온도, 농도조건을 통해 계산된 명목반응속도 대비 실제반응속도의 비로 정의된다. 따라서 수증기/메탄 개질반응의 촉매유효도를 적절히 예측할 수 있는 경우, 촉매층 내부에서 일어나는 열전달, 물질전달, 개질반응에 대한 복잡한 계산없이 명목반응속도와 촉매유효도의 곱으로 실제 반응속도를 효율적으로 예측할 수 있다.

이러한 논의에 따라 본 연구그룹에서는 저압의 수증기/메탄 개질공정에 대하여(1~3 bar, 600~800°C, S/C비 2~4) 니켈촉매의 촉매유효도 상관식을 구형펠릿(Spherical Pellet) 및 워시코트층(Washcoat Layer)에 대하여 제안한 바 있다.^[10~12] 본 연구에서는 Jeong 등^[12]이 제안한 워시코트 촉매층에 대한 촉매유효도 상관식을 적용하여 마이크로 채널형 수증기/메탄 개질기에 대한 간략화된 1차원 해석모델을 개발하였다. 개발된 1차원 해석모델의 타당성은 동일한 개질기에 대한 CFD 해석결과와의 비교를 통해 검증하였다. 이후 다양한 운전조건의 변화 등에 대한 파라미터 해석결과도 비교하여 제시하였다.

본 연구에서 고려한 1~3 bar의 압력은 수소충전소(HRS, Hydrogen Refueling System)에서 일반적으로 활용되는 개질압력 범위에 비해 상당히 낮다. 따라서 저압의 도시가스를 활용한 주거용 및 상업용 수소연료전지 발전시스템에 더욱 적합한 조건이다.^[13] 또한 본 연구에서 고려한 마이크로 채널형 개질기는 미세한 크기의 유로 벽면에 얇은 촉매 워시코트층을 형성하며, 그 구조에 따라서 평판형 개질기(Plate Reformer), 모노리스형 개질기(Monolithic Reformer), 마이크로튜브형 개질기(Microtubular Reformer) 등을 포함한다. 마이크로 채널형 개질기는 기존의 고정층 개질기(Fixed Bed Reformer)와 비교하여 열전달, 물질전달을 크게 향상시킬 수 있는 장점이 있어 개질공정 강화 및 시스템 소형화가 용이하며 이에 따라 많은 연구가 이루어지고 있다.^[14,15]

2. 해석모델

2.1 해석영역

본 연구에서 고려한 2차원 마이크로 채널형 수증기/메탄 개질기의 형상모델을 Fig. 1(a)에 나타내었다. 높이가 1.5 mm인 마이크로 채널이 두께 0.2 mm인 지지판(Substrate) 2개 사이에 형성되어 있으며, 지지판의 내표면에 50 μm 두께의 니켈 워시코트 촉매층이 적용되어 있다. 개질기체는 좌측의 입구를 통해 유입되어 0.1 m 길이의 마이크로 채널을 유동하면서 메탄(CH₄: 1), 수증기(H₂O: 2) 분자가 워시코트 촉매층으로 확산되어 들어간다. 이후 개질반응에 의해 생성된 수소(H₂: 3), 일산화탄소(CO: 4), 이산화탄소(CO₂: 5) 분자가 다시 마이크로 채널로 확산되어 빠져나와 개질기체 유동을 따라 우측의 출구를 통해 유출된다. 지지판의 외표면에는 대류열전달에 의한 열공급을 가정하였다.

Fig. 1.

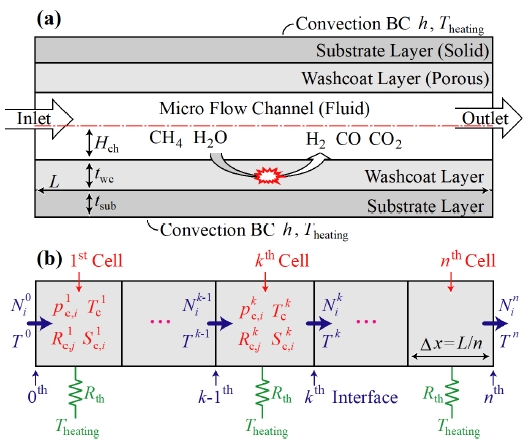
Schematics of an exemplary microchannel steam/methane reformer considered in this study: (a) physical domain and (b) its discretized calculation grid

Fig. 1(a)의 물리적 영역에 대한 1차원 해석모델의 계산 격자계 구성을 Fig. 1(b)에 나타내었다. 해석 격자계는 마이크로 채널형 개질기의 유동방향으로 배치된 n개의 체적셀(1, 2, ⋯, n) 및 n+1개의 경계(0, 1, ⋯, n)로 구성되어 있다. Fig. 1(b)에서 경계에서 계산되는 주요 변수로 개질기체의 온도 T(°C) 및 화학종 i의 몰유량 N_i(mol/s)가 표시되어 있다. 마찬가지로 체적셀에서 계산되는 주요 변수로 온도 T_c(°C), 분압 p_c,i(bar), 개질반응 j의 반응속도 R_c,j(mol/s), 화학종 i의 생성량 S_c,i(mol/s)가 표시되어 있다. 1차원 해석에서는 대칭을 고려하여 채널의 중심선 아래 반 영역(Half Region)만을 고려하였다.

2.2 개질반응

본 연구에서는 다음과 같이 수증기개질(SR), 수성가스화(WGS), 역메탄화(RM)의 전체반응단계(Global Reaction Step)^[16]를 통해 수증기/메탄 개질공정을 고려하였다.

I. 수증기개질(Steam Reforming, SR):

C H 4 + H 2 O ↔ C O + 3 H 2, Δ h = + 206 k J m o l - 1

(1)

II. 수성가스화(Water-Gas Shift, WGS):

C O + H 2 O ↔ C O 2 + H 2, Δ h = - 41 k J m o l - 1

(2)

III. 역메탄화(Reverse Methanation, RM):

C H 4 + 2 H 2 O ↔ C O 2 + 4 H 2, Δ h = + 165 k J m o l - 1

(3)

Xu and Froment(1989)^[16]는 니켈 촉매에 대하여 위와 같은 반응속도를 연구하였으며 반응단계 j에 대한 내재적 반응속도식 r_j(kmol/kg_cat-h)를 다음과 같이 제안하였다.

r I = k I p H 2 2.5 p C H 4 p H 2 O - p H 2 3 p C O K e q, I / D E N 2

(4)

r I I = k I I p H 2 p C O p H 2 O - p H 2 p C O 2 K e q, I I / D E N 2

(5)

r I I I = k I I I p H 2 3.5 p C H 4 p H 2 O 2 - p H 2 4 p C O 2 K e q, I I I / D E N 2

(6)

위 식에서 DEN은 다음과 같다.

D E N = 1 + K C O p C O + K H 2 p H 2 + K C H 4 p C H 4 + K H 2 O p H 2 O p H 2

(7)

위 식에서 k_j 및 K_eq,j는 각각 반응단계 j에 대한 반응속도상수 및 반응평형상수로 다음과 같다.

k I = 4.225 × 1015 exp ⁡ - 240,100 R g T k m o l ⋅ b a r 0.5 k g c a t ⋅ h

(8)

k I I = 1.955 × 106 exp ⁡ - 67,130 R g T k m o l b a r ⋅ k g cat ⋅ h

(9)

k I I I = 1.020 × 1015 exp ⁡ - 234,900 R g T k m o l ⋅ b a r 0.5 k g cat ⋅ h

(10)

K eq, I = e x p ⁡ - 26,830 T + 30.114 b a r 2

(11)

K e q, I I = e x p ⁡ 4,400 T - 4.036

(12)

K e q, I I I = K e q, I K e q, I I = e x p ⁡ - 22,430 T + 26.078 b a r 2

(13)

여기서 K_i는 기체종 i에 대한 흡착계수이다.

K C H 4 = 6.65 × 10 - 4 e x p ⁡ 38,280 R g T ba r - 1

(14)

K H 2 O = 1.77 × 105 e x p ⁡ - 88,680 R g T

(15)

K H 2 = 6.12 × 10 - 9 e x p ⁡ 82,900 R g T ba r - 1

(16)

K C O = 8.23 × 10 - 5 e x p ⁡ 70,650 R g T ba r - 1

(17)

2.3 지배방정식

Fig. 1(b)의 격자계에서 정의된 주요한 경계 변수의 계산을 위한 지배방정식은 화학종보존 및 에너지보존을 고려하여 유도되었다. 즉, 화학종 i의 몰유량 N_i에 대한 지배방정식은 체적셀에서의 생성량 S_c,i을 고려하여 체적셀 k에 대하여 다음과 같이 정리된다.

N i k - 1 + S c, i k = N i k for k = 1, 2, ⋯ n

(18)

단, $N i 0$ 는 채널 입구에서의 화학종 i의 몰유량으로 입구온도 T⁰, 입구압력 $p t 0$ 및 입구몰분율 $x i 0$ 을 통해 결정된다.

주요한 경계 변수인 개질기체의 온도 T에 대한 지배방정식은 외부대류를 통한 가열을 포함하여 체적셀 k에 대하여 다음과 같이 정리된다.

∑ i = 1 5 N i k - 1 h ~ i T k - 1 + T heating - T c k R th = ∑ i = 1 5 N i k h ~ i T k

(19)

여기서 $h ~ i T$ 는 총엔탈피(Total Enthalpy)로 J/mol 단위이며 기준온도 T_ref에서의 화학종 i의 생성엔탈피(Formation Enthalpy) $Δ h ~ f, i$ 와 몰비열 $c ~ i$ 을 통해 다음과 같이 정의된다.

h ~ i T = Δ h ~ f, i + c ~ i T - T r e f

(20)

본 연구에서는 엔탈피 계산의 기준온도 T_ref를 입구온도 T⁰와 동일하게 설정하였다. 또한 식 (19)에서 T_heating은 외부대류의 가열온도, T_c는 체적셀 온도를 의미하며, R_t_h는 외부 대류열저항, 지지판 전도저항, 워시코트 전도저항(전도 길이는 워시코트 두께와 동일하다고 가정)을 합한 총합열저항(°C/W)이다. 참고로 식 (19)에서는 총엔탈피를 고려함으로써 개질반응열이 자동으로 처리된다.

체적셀의 주요 변수인 온도 T_c, 분압 p_c,i은 경계 변수 T 및 N_i를 이용하여 다음과 같이 간단하게 계산되었다.

T c k = T k - 1 + T k 2, p c, i k = 12 p t N i k - 1 N t k - 1 + N i k N t k

(21)

여기서 p_t(bar)는 개질기체의 총 압력으로 마이크로 채널 내부에서 거의 일정하게 유지된다. 또한 N_i/N_t는 경계에서 화학종 i의 몰유량을 총 유량으로 나눈 값으로 몰분율에 대응된다. 따라서 식 (21)은 체적셀에서의 온도와 분압을 체적셀 양쪽 경계값의 평균으로 설정하는 것이다.

체적셀에서의 화학종 i의 생성량 S_c,i는 체적셀에서의 개질반응 j의 반응속도 R_c,j와 반응양론을 고려하여 다음과 같이 계산된다.

S c, C H 4 k = - R c, I k - R c, I I I k

(22)

S c, H 2 O k = - R c, I k - R c, I I k - 2 R c, I I I k

(23)

S c, H 2 k = 3 R c, I k + R c, I I k + 4 R c, I I I k

(24)

S c, C O k = R c, I k - R c, I I k

(25)

S c, C O 2 k = R c, I I k + R c, I I I k

(26)

2.4 촉매유효도

화학종 생성량 S_c,i를 계산하는데 필요한 체적셀 개질반응속도 R_c,j는 다공성 워시코트 촉매층 내부에서 일어나는 개질반응의 결과이다. 이 개질반응속도의 정확한 결정을 위해서는 일반적으로 다공성 매질에서의 복잡한 확산/반응 문제(Diffusion/Reaction Problem)를 풀어야 한다. 그러나 본 연구에서는 워시코트 촉매층에서의 개질반응속도 R_c,j를 촉매유효도 η_j와 촉매층 표면에서의 온도, 농도로부터 계산되는 명목 개질반응속도 R_nom,j(mol/s)를 곱하여 결정하는 방식을 취하였다. 예를 들어 체적셀 k에 대하여 개질반응속도 R_c,j는 다음과 같이 간단하게 결정된다.

R c, j k = η j k × R n o m, j k

(27)

R n o m, j k = 1 3.6 ρ c a t t w c Δ x × r j p c, i k, T c k

(28)

위 식에서 ρ_cat(kg_cat/m³)은 촉매층의 겉보기 밀도(Apparent Density)를, t_wc×Δx×1은 체적셀 내의 워시코트 촉매층 부피(m³)를 나타낸다. 따라서 3.6이란 수는 kmol/h 단위의 반응속도를 mol/s 단위로 변환하는 환산인자이다. 참고로 $r j p c, i k, T c k$ 는 식 (4), (5), (6)으로 계산되는 개질반응 j의 반응속도로 체적셀 k에서의 화학종 분압 $p c, i k$ 및 온도 $T c k$ 의 함수로 계산되었다. 따라서 신뢰성있는 촉매유효도 η_j가 확보되는 경우 워시코트 촉매층 내부에서 발생하는 개질반응속도를 복잡한 계산없이 정확하고 효율적으로 결정할 수 있다.

Jeong et al.(2018)^[12]은 50 μm 내외의 얇은 니켈촉매 워시코트 촉매층에 대하여 다음과 같은 촉매유효도 상관식을 제안하였다.

η I = 1.5 1 + 0.41 ϕ I * 1.88 단, η I ≤ 1

(29)

η I I I = 1.5 1 + 4.14 ϕ I I I * 1.03 단, η I I I ≤ 1

(30)

위 식은 SR(η_I) 반응 및 RM(η_I_I_I) 반응에 대하여 촉매유효도 상관식을 제시한다. Jeong et al.(2018)^[12]은 WGS 반응이 전체 개질반응에서 차지하는 중요성이 낮고 그 반응속도도 일산화탄소(CO)를 생성하는 SR 반응속도에 의존하는 등 거의 평형제한 반응(Equilibrium-limited Reaction)과 같이 거동한다는 점을 고려하여 간단히 η_I_I≈1.0을 사용할 것을 추천하였다. 식 (29), (30)의 $ϕ I *$ 및 $ϕ I I I *$ 는 유효 Thiele 모듈러스 ϕ_I 및 ϕ_I_I_I를 수정하여 얻은 수정 Thiele 모듈러스를 의미하며 다음과 같이 정의된다.^[12]

ϕ I * = ϕ I p t, ∞ 1 ba r 0.18 T ∞ 700 ∘ C - 1.3 S C 3 0.07

(31)

ϕ I I I * = ϕ I I I p t, ∞ 1 ba r - 0.2 T ∞ 700 ∘ C 0.9 S C 3 - 0.6

(32)

수정 Thiele 모듈러스는 온도(600~800°C), 압력(1~3 bar) 및 탄소 대 수증기 비율인 S/C비(2~4) 등 다양한 수증기/메탄 개질조건의 영향을 고려하기 위해 도입되었다.^[12]

유효 Thiele 모듈러스는 명목 반응속도 R_nom,I, R_nom,III 및 명목 메탄확산속도 M_wc,CH₄을 통해 다음과 같이 정의된다.

ϕ I = R n o m, I M n o m, C H 4, ϕ I I I = R n o m, I I I M n o m, C H 4

(33)

위에서 R_nom,I과 R_nom,III는 식 (28)에서 정의된 명목 개질반응속도를 의미하여 명목 메탄확산속도 M_wc,CH₄(mol/s)은 다음과 같이 정의된다.^[12]

M w c, C H 4 k = D C H 4, eff k R g T c k p c, C H 4 k - p c, C H 4, e q k t w c × Δ x

(34)

여기서 p_c,CH₄,eq는 개질압력 p_t, 온도 T_c, S/C비 등 체적셀에서의 국소 개질조건에 따라 결정되는 수증기/메탄 개질반응의 평형 메탄 몰분율을 의미한다. 계산과 관련된 자세한 내용은 Jeong et al.(2018)를 참고하라.

워시코트 촉매층 내부에서 메탄의 유효확산계수 D_CH4,eff는 다음과 같이 정의된다.

D C H 4, e f f = ε / τ 1 D m, C H 4 + 1 D K, C H 4

(35)

위에서 ε은 공극률(Porosity), τ는 굴곡도(Tortuosity)로, ε/τ 인자는 다공성 매질의 공극구조로 인한 확산 단면적의 감소와 확산 길이의 증가를 고려하는 인자이다.

식 (35)에서 D_m,CH4는 다성분확산을 고려한 일반 매질(Plain Medium)에서의 메탄의 유효확산계수를 의미한다. 화학종 i에 대한 유효확산계수 D_m,i는 다음과 같이 계산된다.

D m, i = 1 - x i ∑ j = 1 j ≠ i 5 x j D i j

(36)

위 식에서 x_i는 종 i의 몰분율이고, D_ij(m²/s)는 기체종 i-j 쌍에 대한 이성분 확산계수이다. 본 연구에서는 Fuller et al.(1966)^[17]의 상관식을 이용하여 다음과 같이 D_ij를 결정하였다.

D i j = 10 - 4 0.00143 T 1.75 p t M i j 1 / 2 v i 1 / 3 + v j 1 / 3 2

(37)

여기서 온도 T는 K 단위, 총 압력 p_t는 bar 단위이다. 또 v_i 및 v_j는 확산부피(CH₄: 25.14, H₂O: 13.1, H₂: 6.12, CO: 18.0, CO₂: 26.7)를 나타내며 혼합 분자량 M_ij는 M_ij=2[(1/M_i)+(1/M_j)]^-1로 계산된다. 참고로 CH₄, H₂O, H₂, CO, CO₂의 분자량은 각각 16.043, 18.015, 2.016, 28.010, 44.010 kg/kmol이다.

식 (35)에서 D_K,CH₄는 다공성 매질에서 평균자유행정(Mean Free Path)보다 작은 공극크기 때문에 발생하는 메탄의 누센(Knudsen) 확산계수를 나타낸다. 화학종 i에 대한 누센확산계수 D_K,i는 평균 공극크기 d_pore의 함수로 다음과 같이 계산된다.

D K, i = 972 d pore T M i

(38)

2.5 해석조건

본 연구에서 고려한 마이크로 채널형 개질기의 물리적 특성을 Table 1에서 정리하였다. Table 1에서 제시된 워시코트 촉매층의 겉보기 촉매밀도 ρ_cat=2,355 kg_cat/m³은 Xu and Froment(1989)^[16]의 측정값과 동일하다. 공극률과 굴곡도도 여러 연구자들^[16,18]이 사용한 값을 참고하여 ε=0.5, τ=4.0으로 설정하였다. 또한 Table 2에서는 마이크로 채널형 개질기의 작동조건을 제시하였다. S/C비는 개질기체에 포함된 탄소 대비 수증기의 비율로, 개질기 입구에서의 메탄 몰유량 대비 수증기 몰유량로 정의된다. 본 연구에서는 S/C=3으로 가정하여 $x C H 4 0 = 0.25, x H 2 O 0 = 0.7$ 로 설정되었다(H₂, CO, CO₂의 입구 몰농도는 0).

Table 1.

Physical properties for the reformer

Table 2.

Operating conditions for the reformer

개질기를 통해 수증기/메탄 혼합기체가 흐르면 개질공정이 진행됨에 따라 메탄의 농도가 축방향으로 점차 감소하게 된다. β_CH₄는 메탄전환율(Methane Conversion)로 유동채널의 입구 및 출구에서의 메탄 몰유량 N_CH₄,in 및 N_CH₄,out을 통해 다음과 같이 정의된다.

β C H 4 = N C H 4, i n - N C H 4, out N C H 4, i n = 1 - N C H 4, out N C H 4, i n

(39)

메탄전환율 β_CH₄는 수증기/메탄 개질기의 수소생산 효율성에 대한 성능지표(Performance Index)로 중요하다.

마이크로 채널형 개질기에 대한 간략화된 1차원 모델을 이용한 해석은 축방향으로 100개의 체적셀(n=100)을 배치하여 수행되었다. 위에서 설명한 지배방정식과 열전달, 물질전달 물성값, 수증기/메탄 개질반응식은 비선형방정식 솔버 EES(Engineering Equation Solver, F-Chart Software) 프로그램^[19]을 활용하여 해석하였다. 참고로 본 연구에서 고려한 것과 같은 plug flow 반응기 모델은 단순화에 따른 한계가 있으나 질량 및 에너지보존을 정확히 고려하면서 주요 공정변수의 영향을 적은 계산비용으로 빠르게 평가할 수 있는 장점을 가진다.^[20] 검증을 위한 비교데이터는 동일한 마이크로 채널형 개질기 형상에 대하여 전산유체역학(CFD, Compuational Fluid Dynamics) 해석툴인 ANSYS Fluent^[21]를 이용한 상세해석을 통하여 얻어졌다. CFD 해석모델은 정확한 결과를 얻기 위하여 유동이 흐르는 축방향으로 200개의 체적셀을 배치하고 수증기/메탄 개질반응이 발생하는 얇은 워시코트 촉매층에 두께방향으로 50개의 조밀한 체적셀을 배치하여(유로 반채널 높이에는 20개의 체적셀 배치) 해석하였다. CFD 해석모델의 구성에 대한 보다 자세한 정보는 Oh et al.(2022)^[22]을 참고하라.

3. 결과 및 고찰

해석모델의 검증을 위하여 간략화된 1차원 모델 및 CFD 모델 모두 Fig. 1 및 Table 1, 2에서 제시한 바와 같이 동일한 마이크로 채널형 개질기 형상 및 운전조건에 대하여 해석을 수행하였다. 계산에 사용된 격자계를 간단히 비교하면, 1차원 간략모델의 경우 100개의 체적셀이 해석영역에 배치되었으며 CFD 상세모델의 경우 15,000개의 체적셀이 사용되었다. CFD 해석결과의 정확성은 격자비의존성검사(Grid Independence Test)를 수행하여 해가 충분히 수렴하였음으로 확인하였다.

먼저 수증기/메탄 개질기의 수소생산 효율성의 지표인 메탄전환율 β_CH₄의 경우 기본조건에서 정확한 CFD 모델은 84.2%로 예측하는 데 비해 간략화된 1차원 모델은 85.5%로 대략 1.3% 포인트 더 높게 예측하고 있다. 그러나 앞에서 설명한 격자계의 차이 및 그에 따른 계산시간의 차이를 고려하면 전체적인 수소생산 효율성을 빠르고 비교적 정확하게 예측할 수 있어 간략화된 1차원 해석모델의 실용성을 충분히 확인할 수 있다. 참고로 정리하면 간략화된 1차원 해석모델의 경우 계산에 5초 이내의 시간이 소요되었으며 반면에 CFD 해석모델의 경우 대략 23분 정도의 계산시간이 소요되었다.

이어서 Fig. 2에서 마이크로 채널형 개질기의 유동 방향 x축을 따른 온도분포의 해석결과를 비교하였다. CFD 해석결과로 마이크로 채널의 중심선(Channel Centerline)에서 온도분포와 워시코트층의 온도분포를 기호로 나타내었고 1차원 해석모델의 경우 식 (19)로 계산되는 대표온도 T를 실선으로 나타내었다. 여기서 1차원 해석모델의 간략화로 인해 대표온도 T는 특정 위치에서의 온도로 보기 어렵다. 식 (19)에서 대표온도 T는 개질반응에 따른 에너지보존의 측면에서는 혼합기체의 온도로 취급되고 반면에 외부대류에 의한 반응열 공급의 측면에서는 워시코트 촉매층의 온도로 취급되고 있다.

Fig. 2.

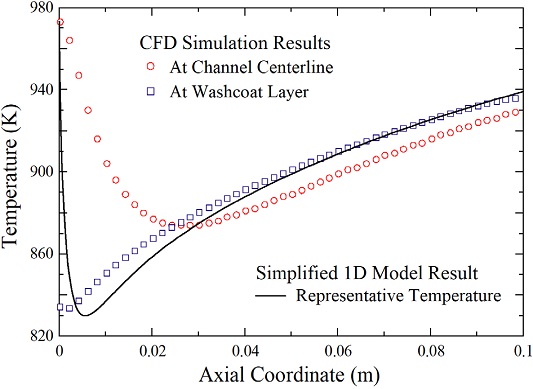
Comparison of simplified 1D model results with detailed CFD simulation results: distribution of temperature T along the axial coordinate

Fig. 2에서 전체적인 온도분포를 살펴보면 개질기 입구 근처에서 온도가 급격히 감소하였다가 출구로 가면서 점차 증가하는 경향이 확인된다. 수증기/메탄 개질반응은 강한 흡열반응으로 개질기 입구 근처의 큰 반응율에 의해 온도가 급감하였다가 외부 표면을 통한 가열에 의해 온도가 점차 회복되는 것으로 판단된다. Fig. 2에서 1차원 해석모델의 대표온도는 개질기 입구 바로 근처를 제외하고는 워시코트층의 온도와 매우 유사한 거동을 보이고 있음을 관찰할 수 있다. 이를 통하여 1차원 해석모델의 대표온도를 통해 마이크로 채널형 개질기 내부 워시코트층의 대략적인 온도분포를 적절하게 예측할 수 있음을 확인하였다.

Fig. 3에서는 마이크로 채널형 개질기를 흐르는 혼합기체 몰분율의 축방향 분포를 비교하였다. CFD 해석결과는 마이크로 채널의 중심선에 대하여 얻어진 기체종의 몰분율을 기호로 표시하였으며 실선으로 표시된 1차원 해석결과와 비교하여 나타내었다. 1차원 해석모델이 예측하는 몰분율 분포는 전체적으로 CFD 해석결과와 비교적 잘 일치하고 있으며 특히 앞서 Fig. 2에서 관찰한 바와 같이 개질기 입구 근처에서 오차가 크지만 출구로 가면서 그 오차가 점차 줄어드는 경향을 관찰할 수 있다. 전체적으로 간략화된 1차원 해석모델이 마이크로 채널형 개질기의 개질기체 농도분포는 매우 잘 예측할 수 있음을 확인할 수 있다.

Fig. 3.

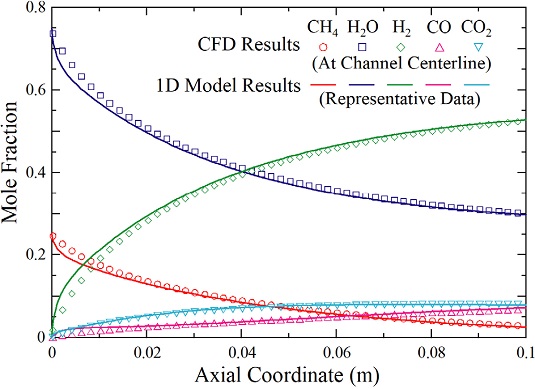
Comparison of simplified 1D model results with detailed CFD simulation results: distribution of species mole fraction xi along the axial coordinate

다음으로 Fig. 4에서는 마이크로 채널형 개질기 유동방향을 따라서 개질공정의 주요한 반응인 수증기개질(SR), 수성가스화(WGS) 및 역메탄화(RM)의 반응속도 분포를 나타내었다. Fig. 4에서 나타낸 반응속도는 mol/m²-s단위로 워시코트 촉매층의 겉보기 표면적(Nominal Surface Area) 기준으로 정리된 반응속도 r_A,j을 의미한다. 일반적으로 개질반응은 반응물인 메탄(CH₄)과 수증기(H₂O)가 풍부한 개질기의 입구근처에서 가장 빠르게 일어나며 이러한 경향은 Fig. 4에서 잘 확인된다. CFD 해석결과와 1차원 해석결과의 차이는 입구 근처에서 가장 크게 나타나고 출구로 가면서 점차 줄어들게 된다. Fig. 2나 Fig. 3에서 개질기 입구 근처에서 관찰되는 온도나 몰분율을 큰 차이는 입구 근처에서의 반응속도의 큰 차이에 그 원인이 있음을 확인할 수 있다.

Fig. 4.

Comparison of simplified 1D model results with detailed CFD simulation results: distribution of area-specific reaction rate rA,j along the axial coordinate

Fig. 4에서 WGS 반응의 반응속도의 경우 입구 근처에서의 거동이 CFD 해석결과와 1차원 모델의 결과가 완전히 다름에 주의하라. 앞서 식 (29), (30)에서 SR 및 RM 반응의 촉매유효도 상관식을 제시하면서 설명하였듯이, 본 연구에서는 WGS 반응에 대한 촉매유효도를 Jeong et al.(2018)^[12]의 추천에 따라 간단히 η_II≈1.0로 설정하여 해석하였다. 이러한 단순화의 이유로 상세한 CFD 해석의 결과와는 입구 근처에서는 상당한 차이가 있으나, 수증기/메탄 개질공정의 전체적인 해석 측면에서는 그 영향이 그리 크지 않음이 관찰되며 그 타당성을 확인할 수 있다.

전체적으로 Fig. 2, 3, 4의 기본조건에 대한 해석결과에서 마이크로 채널형 개질기의 출구로 갈수록 CFD 해석결과와 1차원 해석결과가 더 비슷해지는 것을 관찰할 수 있다. 이러한 경향의 이유 중 하나는 수증기/메탄 개질반응이 평형상태가 존재하는 평형반응으로 개질기가 커서 충분한 반응시간이 지나고 나면 결국 평형상태에 도달하기 때문이다. 1 bar, 700°C, S/C=3의 기본조건의 경우, 평형 메탄전환율은 97.2%로 수증기/메탄 개질공정이 진행됨에 따라서 결국 이 메탄전환율로 수렴해 가게 되는 것이다.

기본 개질조건에서의 모델의 검증에 이어서 운전조건의 변화에 따른 마이크로 채널형 수증기/메탄 개질기의 성능변화 고찰 및 CFD 상세모델과 1차원 간략모델의 해석결과 비교를 수행하였다. Fig. 5에서는 개질기 입구에서의 혼합기체의 유동속도 u⁰를 1, 2, 4, 8 m/s로 변화시키면서 해석을 수행하여 마이크로 채널을 따른 메탄전환율 β_CH₄의 변화를 그래프로 나타내었다. 식 (39)에서 정의한 대로 메탄전환율은 입구에서 공급된 메탄의 몰유량 대비 분해된 메탄의 몰유량의 비로 정의된다. CFD 해석의 메탄전환율은 마이크로 채널에 1 cm 간격으로 생성된 단면을 흐르는 메탄의 몰유량을 구한 후 후처리 과정을 통해 구하였다.

Fig. 5.

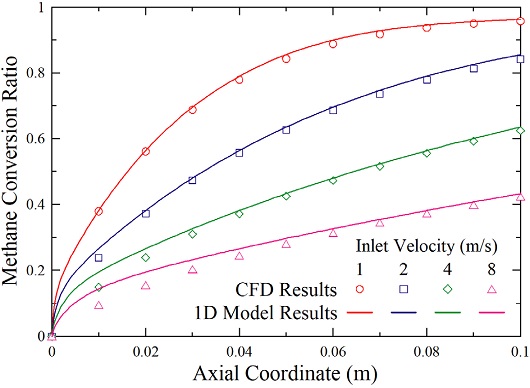
Comparison of simplified 1D model results with detailed CFD simulation results: Effects of inlet fluid velocity u0 on evolution of methane conversion

Fig. 5에서 유동속도가 증가함에 따라서 메탄전환율이 감소하는 경향이 관찰된다. 이것은 유동속도가 수증기/메탄 혼합기체가 개질기 내부를 흐르는 체류시간(Residence Time)을 결정하기 때문이다. 1 bar, 700°C, S/C=3의 기본조건의 평형 메탄전환율이 97.2%라는 점을 고려하면, u⁰=1 m/s의 입구속도 조건에서 메탄전환율은 대략 96% 정도로 예측되어 수증기/메탄 혼합기체가 평형상태에 거의 도달할 만큼 충분한 체류시간이 확보되었음을 알 수 있다. 그러나 수소생산의 측면에서 생각해보면 낮은 유동속도와 그에 따른 높은 메탄전환율이 반드시 바람직한 것은 아니다. 예를 들어 Fig. 5에서 u⁰=2 m/s의 입구속도 조건에서 메탄전환율은 대략 85% 정도로 예측되므로 u⁰=1 m/s인 경우와 비교하면 대략 77% 더 많은 메탄의 분해가 일어나게 된다. 따라서 적절한 입구속도 조건의 선정을 통해 수증기/메탄 개질공정의 최적화가 필요함을 확인할 수 있다.

Fig. 5에서 1차원 해석모델로 얻어진 메탄전환율 분포는 CFD 해석결과와 비교하여 비교적 잘 일치하고 있음을 관찰할 수 있다. 앞서 살펴본 결과 그래프들과 마찬가지로 가장 큰 오차는 개질기 입구 근처에서 나타나는 것이 관찰된다. 정확한 수치 비교를 위하여 마이크로 채널형 수증기/메탄 개질기의 총 메탄전환율의 해석결과를 Table 3에서 비교하였다. 1~8 m/s의 입구속도 조건에 대하여 CFD 해석모델과 1차원 해석모델은 최대오차가 1.3% 포인트 이내로 잘 일치함을 확인하였다.

Table 3.

Summary of methane conversion ratio from parametric studies of varying inlet velocity u0 and convective heat transfer coefficient h

다음으로 외부가열 조건의 변화에 따른 메탄전환율의 거동을 Fig. 6에서 살펴보았다. 본 연구에서는 마이크로 채널형 수증기/메탄 개질기의 지지판 외표면에서 대류열전달을 통해 개질에 필요한 반응열이 공급되는 상황을 고려하였다. 따라서 가열온도 T_heating을 700°C로 고정하고 대신에 대류열전달계수 h를 50, 100, 200, 400 W/m²-K으로 변화시키면서 해석을 수행하여 마이크로 채널 축방향으로의 메탄전환율의 변화를 Fig. 6에 나타내었다. Fig. 6에서 1차원 간략모델과 CFD 상세모델 모두 동일하게 대류열전달계수가 증가함에 따라서 메탄전환율이 증가함을 예측하고 있다. 참고로 Table 3에서 간략화된 1차원 해석모델의 총 메탄전환율 예측값은 CFD 상세모델의 해석과 비교하여 최대오차가 1.4% 포인트 이내로 나타났다.

Fig. 6.

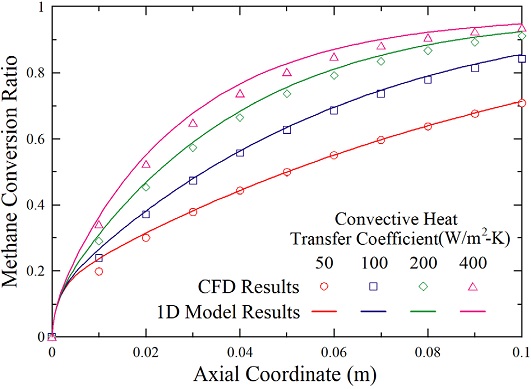
Comparison of simplified 1D model results with detailed CFD simulation results: Effects of convective heat transfer coefficient h on evolution of methane conversion

수증기/메탄 개질반응은 강한 흡열반응이므로 반응열의 공급이 원활할수록 개질공정이 더욱 빠르게 진행되어 그 결과로 메탄전환율이 증가하는 경향이 나타나는 것이다. 그러나 대류열전달계수가 200 W/m²-K 이상이 되면 수증기/메탄 개질반응은 거의 평형상태에 도달하여 대류열전달계수를 증가시켜도 미미한 메탄전환율의 증가만이 나타나게 된다. 수증기/메탄 개질공정은 열전달, 물질전달, 유체유동, 반응속도 및 평형상태 모두에 영향을 받는 매우 복합적인 과정이다. 따라서 단순히 열전달 속도, 물질전달 속도 또는 촉매반응 속도(예를 들어 더 많은 촉매를 사용하여) 중 한가지 조건만을 향상시켜서 개질공정의 진행속도(수소의 생산속도)를 크게 증가시키기 어렵다. 따라서 다양한 공정변수의 영향에 대한 적절한 해석을 통해 최적화된 설계 및 운전조건을 수립하는 것이 중요하다.

4. 결 론

본 연구에서는 촉매유효도 상관식을 이용하여 마이크로 채널형 수증기/메탄 개질기를 효율적으로 해석할 수 있는 간략화된 1차원 모델을 개발하였다. 와시코트 촉매층 표면에서의 온도 및 농도조건으로 계산되는 명목반응속도에 촉매유효도를 곱하여 실제 반응속도를 결정하는 방식을 통해 촉매층 내부에서의 일어나는 복잡한 전달현상 및 개질반응에 대한 계산비용을 줄일 수 있다. 본 연구에서 제안한 간략화된 1차원 해석모델의 정확도는 상세한 CFD 해석모델을 이용하여 동일한 마이크로 채널형 수증기/메탄 개질기의 작동을 계산하고 그 결과를 비교함으로써 검증하였다. 간략화된 1차원 해석모델은 매우 작은 계산비용으로 마이크로 채널형 개질기 내부에서 일어나는 수증기/메탄 개질공정의 전반적인 거동을 잘 예측함을 확인하였다.

기본조건 외에 추가로 개질기 입구에서의 유동속도 및 외부가열의 대류열전달계수를 변화시키는 경우에 대한 파라미터 연구를 진행하였다. 이 경우에도 간략화된 1차원 해석모델은 CFD 해석모델과 비교하여 총 메탄전환율 기준으로 최대오차 1.5% 이내로 전반적인 수증기/메탄 개질공정을 잘 예측하였다. 이러한 연구결과를 통해 본 연구에서 제안하는 간략화된 1차원 해석모델이 마이크로 채널형 수증기/메탄 개질기의 형상설계 및 운전조건 최적화에 활용될 수 있을 것으로 기대한다.

Nomenclature


D_i,eff :	effectiveness diffusivity in the catalyst layer, m²/s
D_ij :	binary diffusivity of i-j species pair, m²/s
D_K,i :	Knudsen diffusivity of species i, m²/s
D_m,i :	effective diffusivity in the flow channel, m²/s
d_pore :	mean pore diameter, m
H_ch :	channel half-height, m
h :	convective heat transfer coefficient, W/m²-K
$h ~ i$ :	total enthalpy of species i, J/mol
$h ~ f, i$ :	formation enthalpy of species i, J/mol
K_eq,j :	equilibrium constant for reaction j
K_i :	adsorption coefficient of species i
K_v :	viscous flow permeability, m²
k_eff :	effective thermal conductivity, W/m-K
k_j :	reaction rate constant for reaction j
M_i :	molecular mass of species i, kg/kmol
M_wc,CH₄ :	nominal methane diffusion rate, mol/s
N_i :	molar flow rate of species i, mol/s
p_i :	partial pressure of species i, bar
p_t :	total pressure, bar
R_j :	reaction rate of reaction j, mol/s
R_g :	universal gas constant, 8.314 kJ/kmol-K
R_nom,j :	nominal reaction rate of reaction j, mol/s
r_j :	reaction rate of reaction j, kmol/kg_cat-h
SC :	steam-to-carbon (S/C) ratio
S_i :	source for species i, mol/s
T :	temperature, °C
t_wc :	washcoat layer thickness, m
t_sub :	substrate layer thickness, m
x_i :	mole fraction of species i

Greek letters


ρ_cat :	apparent catalyst density, kg_cat/m³
β_CH₄ :	methane conversion
ε :	porosity
ϕ_j :	effective Thiele modulus for reaction j
*$ϕ j $ :**	modified Thiele modulus for reaction j
η_j :	effectiveness factor for reaction j
τ :	tortuosity

Superscirpt/Subscript


0 :	inlet value
∞ :	washcoat surface value
c :	cell value

Acknowledgments

본 논문은 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(Grant No. NRF–2019R1F1A1041995)의 연구 결과이며 이에 감사드립니다.

References

Ha, S.J., Choi, J.H., and Oh, S.J., 2022, “Technology competitiveness analysis of new & renewable energy in major countries”, New. Renew. Energy, 18(3), 72-84. [https://doi.org/10.7849/ksnre.2022.0022]
Kim, H.N., and Kim, J.K., 2021, “Development of methane decomposition reactor for hydrogen production using solar thermal energy”, New. Renew. Energy, 17(2), 40-49. [https://doi.org/10.7849/ksnre.2021.0006]
Ryi, S.K., Han, J.Y., Kim, C.H., Lim, H.K., and Jung, H.Y., 2017, “Technical trends of hydrogen production”, Clean Technol., 23(2), 121-132.
Lee, H., Kim, W., Lee, K., and Yoon, W. L., 2018, “Kinetic model of steam-methane reforming reactions over Ni-based catalyst”, Kor. Chem. Eng. Res., 56(6), 914-920.
Zhang, H., Sun, Z., and Hu, Y. H., 2021, “Steam reforming of methane: current states of catalyst design and process upgrading”, Renew. Sustain. Energy Rev., 149, 111330. [https://doi.org/10.1016/j.rser.2021.111330]
O’Hayre, R. P., Cha, S. W., Colella, W., and Prinz, F. B., 2016, “Fuel Cell Fundamentals”, John Wiley & Sons, New York. [https://doi.org/10.1002/9781119191766]
Han, J. R., Park, S. J., Kim, H.T., Lee, S.J., and Lee, J. M., 2022, “Centralized and distributed hydrogen production using steam reforming: challenges and perspectives”, Sustain. Energy Fuels, 6(8), 1923-1939. [https://doi.org/10.1039/D1SE01870A]
Yun, S.G., Cho, H.T., Kim, M.J., Lee, J.W., and Kim, J.H., 2022, “Exergy analysis and heat exchanger network synthesis for improvement of a hydrogen production process: practical application to on-site hydrogen refueling stations”, Trans. Kor. Hydrog. New Energy Soc., 33(5), 515-524. [https://doi.org/10.7316/KHNES.2022.33.5.515]
Tran, A., Aguirre, A., Crose, M., Durand, H., and Christofides, P.D., 2017, “Temperature balancing in steam methane reforming furnace via an integrated CFD/data-based optimization approach”, Comput. Chem. Eng., 104(2), 185-200. [https://doi.org/10.1016/j.compchemeng.2017.04.013]
Baek, S. M., Kang, J. H., Lee, K. J., and Nam, J. H., 2014, “A numerical study of the effectiveness factors of nickel catalyst pellets used in steam methane reforming for residential fuel cell applications”, Int. J. Hydrog. Energy, 39(17), 9180-9192. [https://doi.org/10.1016/j.ijhydene.2014.04.067]
Nam, J. H., 2015, “Effectiveness factor correlations for spherical nickel catalyst pellets used in small-scale steam methane reformers”, Int. J. Hydrog. Energy, 40(16), 5644-5652. [https://doi.org/10.1016/j.ijhydene.2015.02.119]
Jeong, A.R., Shin, D.W., Baek, S.M., and Nam, J.H., 2018, “Effectiveness factor correlations from simulations of washcoat nickel catalyst layers for small-scale steam methane reforming applications”, Int. J. Hydrog. Energy, 43(32), 15398-15411. [https://doi.org/10.1016/j.ijhydene.2018.06.059]
Ko, S.K., and Lee, S.Y., 2023, “A study on the optimization of hydrogen production and purification system for PEMFC”, Trans. Kor. Hydrog. New Energy Soc., 34(1), 1-7. [https://doi.org/10.7316/KHNES.2023.34.1.1]
Tonkovich, A. Y., Perry, S., Wang, Y., Qiu, D., LaPlante, T., and Rogers, W. A., 2004, “Microchannel process technology for compact methane steam reforming”, Chem. Eng. Sci., 59(22-23), 4819-4824. [https://doi.org/10.1016/j.ces.2004.07.098]
Murphy, D. M., Manerbino, A., Parker, M., Blasi, J., Kee, R. J., and Sullivan, N. P., 2013, “Methane steam reforming in a novel ceramic microchannel reactor”, Int. J. Hydrog. Energy, 38(21), 8741-8750. [https://doi.org/10.1016/j.ijhydene.2013.05.014]
Xu, J., and Froment, G. F., 1989, “Methane steam reforming, methanation and water gas shift: I. intrinsic kinetics”, AIChE J., 35(1), 88-96. [https://doi.org/10.1002/aic.690350109]
Fuller, E. N., Schettler, P. D., and Giddings, J. C., 1966, “New method for prediction of binary gas-phase diffusion coefficients”, Ind. Eng. Chem., 58(5), 18-27. [https://doi.org/10.1021/ie50677a007]
Zanfir, M., and Gavriilidis, A., 2003, “Catalytic combustion assisted methane steam reforming in a catalytic plate reactor”, Chem. Eng. Sci., 58(17), 3947-3960. [https://doi.org/10.1016/S0009-2509(03)00279-3]
Klein, S. A., 2018, “Engineering Equation Solver (EES) Manual”, F-Chart Software LLC, Madison.
Choi, S.K., Choi, Y.S., Jeong, Y.W., Han S.Y., and Nguyen Q. V., 2022, “Analysis on the pyrolysis characteristics of waste plastics using plug flow reactor model”, New. Renew. Energy, 18(4), 12-21. [https://doi.org/10.7849/ksnre.2022.0037]
ANSYS Inc, 2022, “ANSYS Fluent User’s Guide”, Release 2022R1, ANSYS Inc, Canonsburg.
Oh, Y. S., Jeong A.R., and Nam, J. H., 2022, “Efficient computational fluid dynamics model for microchannel-type steam/ methane reformers with nickel washcoat catalyst layers based on effectiveness factor correlations”, Trans. Kor. Hydrog. New Energy Soc., 33(6), 749-760. [https://doi.org/10.7316/KHNES.2022.33.6.749]

Parameters	Values
Reformer dimensions
Reformer length, L	0.1 m
Channel half height, H_ch	0.75 mm
Washcoat layer thickness, t_wc	50 μm
Substrate layer thickness, t_sub	0.2 mm
Washcoat layer properties
Catalyst density, ρ_cat	2,355 kg_cat/m³
Porosity, ε	0.5
Tortuosity, τ	4
Mean pore diameter, d_pore	25 nm
Viscous permeability, K_v	1×10^-18 m²
Effective thermal conductivity, k_eff	1 W/m-K
Substrate layer properties
Thermal conductivity, k_sub	20 W/m-K

Parameters	Values
Reforming conditions
Inlet temperature, T⁰	700°C
Inlet velocity, u⁰	2 m/s
Operating pressure, p_t	1 bar
Steam-to-carbon ratio, SC	3.0
Inlet concentration, $x i 0$	CH₄:0.25, H₂O:0.75
Heating conditions
Convection coefficient, h	100 W/m²-K
Heating temperature, T_heating	700°C

Parameter Variations	Methane Conversion
Parameter Variations	CFD Results	1D Results
Inlet velocity u⁰ variation
1 m/s	95.8%	96.3%
2 m/s	84.2%	85.5%
4 m/s	62.4%	63.5%
8 m/s	42.4%	43.2%
Convective coefficient h variation
50 W/m²-K	70.8%	71.4%
100 W/m²-K	84.2%	85.5%
200 W/m²-K	91.1%	92.5%
400 W/m²-K	93.7%	94.7%