MW급 풍력터빈의 피치 구동기의 대역폭에 관한 연구
© 2017 by the The Korean Society for New and Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Power production is one of the main objectives of wind turbines. Pitch control is utilized to adjust the power produced to the rated value when the wind speed is over the rated value. In real wind turbines, pitch actuators, such as an electric motor or hydraulic actuator, are used to control the pitch angle of the blades. As the length of the blades in the MW wind turbines becomes longer, the mass moment of inertia of the blade increases. This means that there is a limitation to the bandwidth of the pitch actuator. In this study, we investigated the reduction of the mean power, power dip, standard deviation of the power, standard deviation of the rotor speed, and rotor overspeed quantitatively according to the bandwidth of the pitch actuator for a 2 MW wind turbine. The simulation results showed that a bandwidth of more than 15 rad/s is appropriate.
Keywords:
Wind turbine, Pitch controller, Pitch actuator, Bandwidth, Power, Rotor speed키워드:
풍력터빈, 피치 제어기, 피치 구동기, 대역폭, 출력파워, 로터 회전속도1. 서 론
풍력터빈은 바람이 가진 에너지가 로터 블레이드를 회전시켜 기계적인 에너지로 전환한 후 발전기를 통해 전기를 생산하는 기계이다. 최근 풍력터빈은 MW급으로 지속적으로 대형화되고 있으며, 로터의 회전속도와 블레이드의 피치각을 모두 조절하는 가변속도-가변피치 형태를 취한다[1,2]. 풍력터빈이 대형화됨에 따라 정격풍속 이상에서 작동하는 피치 제어기가 출력제어와 하중제어 모두의 관점에서 더욱 중요하게 되었다. 풍력터빈의 피치 제어기는 정격풍속 이상이나 정격풍속 근처에서 풍속의 변화에 따라 블레이드의 피치각을 제어하는 방식으로, 출력제어 목적에서는 풍속의 변화에 대하여 풍력터빈의 출력파워를 정격출력으로 유지하기 위한 것이다.
피치 제어기는 출력제어 만을 고려할 때는 단일입출력(SISO) 시스템으로 볼 수 있고, 출력제어 뿐만 아니라 하중제어를 모두 고려할 때는 다중입출력(MIMO) 시스템으로 볼 수 있다. 출력제어 관점에서 정격출력을 유지하기 위하여 피치 제어기는 여러 형태로 설계될 수 있는데, 게인 스케쥴링을 이용한 PI(비례-적분) 제어기가 가장 실용적이다[3-7].
피치 제어기와 관련된 연구결과들은 출력파워의 성능을 향상하기 위한 관점에서 피치 제어기의 구조와 설계에 관한 내용들이 대부분이지만, 피치 구동기의 동특성이 출력파워에 미치는 영향에 대한 구체적인 연구 결과는 아직 제시되지 않았다[3-12]. 실제 피치 구동기는 전기 모터나 유압식 구동기가 이용되는데, 풍력터빈이 MW급으로 대형화됨으로 블레이드의 길이가 매우 길어지고 질량 관성모멘트가 매우 커져서 피치 구동기의 동특성에 직접적인 영향을 미치게 되었다. 그러므로 피치 제어기의 동특성뿐만 아니라 피치 구동기의 동특성을 함께 파악하는 것이 필요하다. 실제 피치 제어기의 대역폭과 피치 구동기의 대역폭을 어떻게 설정하는가에 따라 풍력터빈의 출력파워의 성능에 미치는 영향이 달라진다.
본 논문은 피치 구동기에 대한 대역폭의 설정에 관한 것으로, 피치 구동기의 대역폭이 풍력터빈의 출력파워와 로터속도의 응답에 미치는 영향을 수치실험을 통하여 정량적으로 확인하고자 한다. 2MW급 풍력터빈을 대상으로 IEC 규정의 난류풍속을 이용하여 수치실험을 수행하여 피치 구동기의 대역폭에 따른 풍력터빈의 응답을 정량적으로 살펴본다. 수치실험은 Matlab/Simulink를 이용하고, 풍력터빈의 모델은 출력제어를 위해 필요한 1-질량 모델을 고려한다. 피치 제어기는 블레이드의 피치각에 대하여 게인-스케쥴링이 되는 PI 제어기를 적용한다. 피치 제어기의 대역폭은 MW급 풍력터빈과 풍속의 특성이 반영된 실제적인 면을 고려하여 1rad/s로 둔다. 피치 구동기의 동특성은 실제와 가까운 2차 시스템을 고려한다. 피치 구동기에 대한 대역폭의 설정에 따른 풍력터빈의 출력파워와 로터속도의 응답특성을 분석하고, 출력제어 관점에서 실제 피치 구동기의 대역폭이 어느 정도가 바람직한지를 보이고자 한다.
2. 풍력터빈 모델
2.1 2MW 풍력터빈 모델 파라미터
풍력터빈은 블레이드, 로터, 회전축, 기어박스, 타워 등 여러 가지 구성요소들로 이루어진 복합시스템이다. 본 논문에서는 2MW 풍력터빈을 대상으로 연구를 수행하였다. 2MW 풍력터빈 모델은 1-질량 모델을 고려하여 Matlab/Simulink에서 구현하여 수치실험을 수행하였다. 2MW 풍력터빈의 기본 파라미터 값들은 Table 1과 같다[13]. Table 1에서 Cp,max는 최대출력계수, λopt는 최적 주속비, R은 로터의 회전반경, Jr은 로터의 질량 관성모멘트, Jg는 발전기의 질량 관성모멘트, Br은 로터의 감쇠, Ngb는 증속기의 기어비이다.
2.2 1-질량 모델
풍력터빈을 운동 방정식으로 표현하게 되면 고차의 운동 방정식으로 표현할 수 있다. 하지만 본 논문에서는 출력제어만을 다루기 때문에 1-질량 모델로 운동 방정식을 표현한다. 1-질량 모델은 기어박스가 있는 풍력터빈에 대해서 기어박스의 기어비만 고려하고 회전축의 강성과 감쇠는 고려하지 않는 운동방정식을 식 (1)과 같이 발전기 측에서 등가의 물리적인 값으로 표현된다.
| (1) |
여기서 등가 회전관성 모멘트(Jeq)는 식 (2)와 같고, 등가감쇠(Beq)는 식 (3)과 같고, 등가의 공력 토크(Teq)는 식 (4)와 같다. Tg는 발전기 토크이고 Ωg는 발전기 회전속도로 로터 속도(Ωr)가 증속기의 기어비(Ngb)만큼 증속된 속도이다.
| (2) |
| (3) |
| (4) |
여기서 Tr은 공력 토크이고 식 (5)과 같이 표현된다.
| (5) |
여기서 λ는 주속비, β는 블레이드의 피치각, V는 허브에서의 풍속, ρ는 공기밀도이다. 주속비(λ)는 풍속(V)에 대한 블레이드 끝단에서의 선속도(R×Ωr)의 비이다.
식 (5)의 공력 토크는 바람에 의해 로터에 작용하는 회전 토크를 의미한다. 공력 토크에 의해 풍력터빈은 회전을 하게 되는데, 식 (1)의 운동방정식은 공력 토크가 로터의 회전 속도로 변환되는 동적 모델이다.
2.3 난류풍속
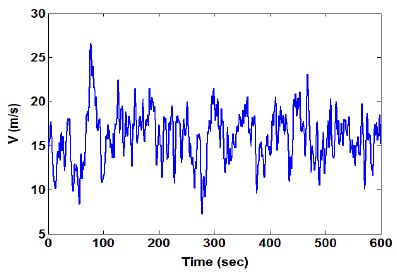
실제와 유사한 풍속을 사용하여 풍력터빈 제어시스템의 성능을 평가하는 것은 매우 중요하다. 풍속의 특성은 통계적인 방법을 이용하여 예측할 수 있는데, Van der Hoven에 의한 풍속 특성 스펙트럼과 Von Kalman 모델을 이용하면 난류강도를 조절할 수 있는 풍속 생성이 가능하다[4,5]. 본 논문의 수치실험에서 사용한 풍속은 ICE 규정[14]에 Class A에 해당하는 것으로 Fig. 1과 같이 10분 동안의 평균풍속은 16m/s이고 난류강도는 17.6%인 난류풍속을 사용하였다. 난류풍속의 평균풍속이 정격풍속 이상이지만 평균 출력파워에서 출력강하가 발생하는 주된 이유는 풍속이 일정시간 동안 정격이하로 크게 줄어들기 때문이다. 그러므로 고려된 Fig. 1의 난류풍속은 이를 확인하기에 적당함을 알 수 있다.
3. 풍력터빈의 출력 제어기
3.1 토크 제어기
토크 제어기는 풍속의 크기에 따라 최적 주속비(λopt)를 얻기 위하여 토크-속도의 정상상태 관계특성을 나타내는 식 (6)를 이용하여 발전기의 토크(Tg)를 발전기의 회전속도(Ωg)의 제곱에 비례하도록 제어하는 것으로 비선형 제어 방법이다.
| (6) |
여기서 Kopt는 최적모드게인으로 발전기의 토크와 발전기의 회전속도 사이의 이차특성을 나타내는 계수값으로 식 (7)과 같다.
| (7) |
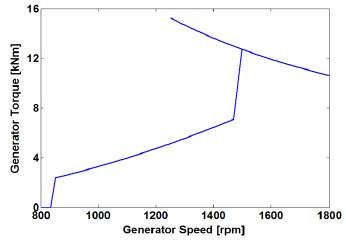
토크 제어기의 구현방법은 Fig. 2와 같이 정격풍속 이하인 경우는 미리 계산된 순람표(Lookup Table)로 사용하여 발전기 토크를 생산한다. 그리고 정격풍속 이상인 경우는 일정한 정격출력이 생산되도록 발전기 토크 크기를 변화시키는 제어 방법을 적용한다. 식 (6)의 최적모드게인을 적용하는 토크 제어기는 비선형 제어 방법이어서 폐루프 토크 제어계의 주파수 응답을 해석적 접근으로 알 수 없지만, 시간 응답 결과를 이용하여 간접적으로 확인할 수는 있다. 고려된 2MW 풍력터빈의 경우 시간 응답을 통하여 시상수가 약 9초인 것으로 확인되었다[15,16]. 그러므로 폐루프 토크 제어계에 대한 주파수 응답의 절점주파수는 약 0.11rad/s이다.
3.2 피치 제어기
풍력터빈의 피치 제어기는 Fig. 3과 같은 속도제어루프 형태의 PI 제어기와 피치 게인-스케쥴링(GS)을 사용하였으며, 피치 제어기는 발전기의 회전속도(Ωg)를 피드백하여 기준입력인 발전기 정격회전속도(Ωref)와의 오차를 PI 제어기를 통해 정격 풍속이상에서 피치각을 조절하는 방법이다. 피치 PI 제어기 설계 시에는 식 (1)의 1-질량 모델로 표현된 운동 방정식에서 공력토크(Tr)를 풍속에 따라 선형화한 결과를 이용한다.
1-질량 모델의 선형화된 운동 방정식은 식 (8)과 같다. 식 (8)을 이용하여 피치각에 대한 발전기 회전속도(Ωg)의 전달함수 G(s)을 식 (9)과 같이 표현할 수 있다. 식 (10)는 PI 제어기의 전달함수 C(s)을 나타내고 있다.
| (8) |
| (9) |
| (10) |
여기서 Kp는 PI 제어기의 비례게인, Ki는 PI 제어기의 적분게인, Nβg는 피치각의 비선형 파라미터이다.
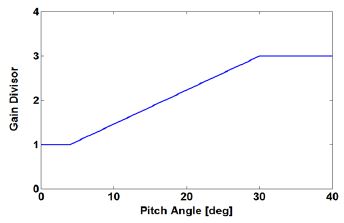
피치 게인-스케쥴러의 개념은 풍속이 증가할수록 Nβg의 절대값이 커져서 고유진동수가 증가하기 때문에 고정된 PI 게인값을 사용하는 것이 아니라 풍속이 증가할수록 작은 PI 게인값을 사용하기 위해 게인제수(Gain Divisor)를 이용하여 PI 게인값을 줄여주는 방법이다. 게인제수는 Fig. 4와 같이 피치각에 따라 결정되도록 설계했다.
3.3 피치 제어기의 대역폭
피치각의 변화에 따른 풍력터빈의 응답을 결정하는 것은 피치 제어기의 대역폭을 어떻게 설정하는가에 따라 달라진다. 바람 특성을 고려하여 풍속의 변화에 대하여 피치 제어기를 빠르게 작동하는 것이 필요하다. 출력제어인 경우 대역폭이 크면 출력파워가 좋아진다. 그러나 피치 제어기의 대역폭을 증가시키면 타워를 가진할 수 있기 때문에 무한정으로 대역폭을 높일 수는 없다. MW급 풍력터빈의 피치 제어기의 대역폭을 약 1rad/s정도 설정하면 타워를 가진하지 않고 풍속의 변화에 따라 빠르게 작동할 수 있는 것으로 알려져 있다[6,17].
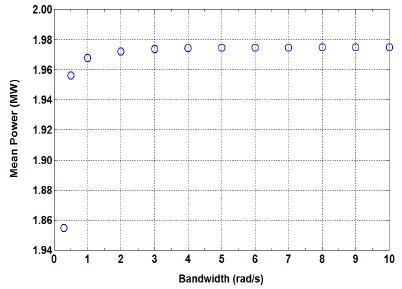
2MW 풍력터빈을 대상으로 피치 제어기의 대역폭에 따른 출력파워의 응답을 확인해 보았다. 수치실험에서 사용된 풍속은 Fig. 1의 난류풍속이다. Fig. 5는 피치 제어기의 대역폭에 따른 평균출력을 보여 준다. 대역폭이 무한대인 경우 평균출력은 1.975MW이고 비교 시의 기준으로 두었다. 대역폭이 10rad/s인 경우 평균출력은 1.975MW이고, 대역폭이 3rad/s 이상이면 평균출력의 변화가 거의 없음을 확인할 수 있다. 그러나 2~3rad/s 사이에 타워의 1차 모드가 존재함으로 피치 제어기의 대역폭을 2rad/s이상으로 사용할 수 없다. 그러므로 실제 피치 제어기의 대역폭을 2rad/s 이하로 설정하는 것이 필요하다. 대역폭이 0.3rad/s인 경우 평균출력은 1.855MW로 출력강하가 6.1%로 매우 크다. 대역폭이 0.5rad/s인 경우 평균출력은 1.956MW로 0.96%의 출력강하가 있고, 대역폭이 1rad/s인 경우 평균출력은 1.968MW로 0.35%의 출력강하가 있다. 그러므로 대역폭을 0.5rad/s 이하로 두면 평균출력이 매우 좋지 않으나, 대역폭을 1rad/s로 두면 평균출력의 강하는 0.4% 정도 이내임을 확인할 수 있다.
4. 피치구동기의 대역폭
4.1 피치 구동기의 동특성
피치 시스템은 피치 제어기와 피치 구동기를 포함한 피치 제어에 관련한 모든 요소들을 포괄하는 의미이다. 여기서 피치 시스템의 동특성이란 피치 시스템의 구동에 관련한 모든 요소들을 포함하면서 특히 가장 크게 영향을 미치는 피치 구동기를 염두에 둔 것이다. 최근 풍력터빈이 대형화되면서 블레이드의 질량 관성모멘트가 증가하고 있다. 블레이드의 질량 관성모멘트는 피치 구동기에 직접적인 영향을 미치므로 풍력터빈이 대형화될수록 피치 구동기의 동특성을 파악하는 것은 반드시 필요하다.
본 논문에서는 피치 구동기의 대역폭에 따른 출력 응답(출력파워의 평균, 출력파워의 표준편차, 로터속도의 평균, 로터속도의 표준편차, 로터속도의 과속 등) 특성을 정량적으로 확인해 보았다. 수치실험에서 피치 제어기의 대역폭은 앞의 3.3절에서 살펴 본 것과 같이 실제적인 면을 고려하여 1rad/s로 설정하였다. 그러므로 피치 제어기에 대한 폐루프계의 주파수 응답의 절점주파수는 1rad/s인 경우를 고려한 것이다. 피치 구동기의 동특성은 2차 시스템을 고려하였고 이를 전달함수 형태로 표현하면 식 (11)과 같다.
| (11) |
여기서 ωn,p와 ζp는 각각 피치 구동기의 고유진동수와 감쇠비이다. 감쇠비 ζp는 0.7로 고정하고 피치 구동기의 대역폭의 변화에 따라 풍력터빈의 출력 응답을 살펴보았다. 2차 시스템인 피치 구동기의 대역폭은 식 (12)와 같다.
| (12) |
대역폭은 주파수 전달함수의 크기가 -3dB가 되는 주파수로 정의된다. 대역폭은 시스템의 응답속도와 밀접한 관계가 있어 대역폭이 넓을수록 응답속도가 빠름을 의미한다.
4.2 피치 구동기의 대역폭에 따른 응답
피치 제어기의 대역폭은 1rad/s로 두고 피치 구동기의 대역폭은 4rad/s부터 20rad/s까지의 범위에 대하여 수치실험을 수행하여 응답을 확인하였다. 피치 구동기를 고려하지 않은 경우(피치 구동기의 대역폭이 무한대인 경우)의 응답을 기준으로 피치 구동기의 유한한 대역폭이 출력파워에 미치는 영향을 살펴본다. Table 2와 Fig. 6~13은 피치 구동기의 대역폭에 따른 발전기의 출력파워와 로터속도의 응답에 대한 정량적인 값을 보여준다. 출력파워의 평균, 표준편차, 파워딮(Power Dip)과 로터속도의 평균, 표준편차, 과속(Overspeed) 모두의 응답을 고려하면 피치 구동기의 대역폭은 약 15rad/s이상인 경우는 응답의 변화가 없고 대역폭이 무한대인 경우(피치 구동기의 동특성이 고려되지 않는 경우)의 응답과 거의 일치함을 확인할 수 있다.
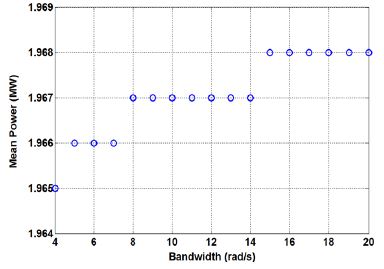
피치 구동기의 대역폭에 따른 출력파워의 평균과 표준편차를 먼저 살펴보자. Fig. 6은 평균 출력파워를, Fig. 7은 평균 출력파워의 감소율을, 그리고 Fig. 8은 출력파워의 표준편차를 보여준다.
평균 출력파워의 경우 피치 구동기의 대역폭이 15rad/s 이상인 경우는 평균출력이 1.968MW로 대역폭이 무한대인 경우의 평균출력과 같음을 확인할 수 있다. 피치 구동기의 대역폭이 4rad/s인 경우는 평균출력은 1.965MW로 출력강하가 0.15%이고, 대역폭이 10rad/s인 경우는 평균출력은 1.967MW로 출력강하가 0.05%이고, 대역폭이 15rad/s 이상인 경우는 평균출력은 1.968MW로 출력강하가 0%이다. 피치 구동기의 대역폭이 평균 출력파워에 미치는 영향은 작음을 확인할 수 있는데, 대역폭이 5rad/s이면 평균 출력파워의 감소율을 0.1% 이내로 작고, 대역폭이 15rad/s 이상이면 평균 출력파워의 감소가 없음을 확인할 수 있다.
출력파워의 표준편차의 경우 피치 구동기의 대역폭이 13rad/s 이상인 경우는 표준편차가 0.141MW로 대역폭이 무한대인 경우의 표준편차와 같음을 확인할 수 있다. 피치 구동기의 대역폭이 4rad/s인 경우는 출력파워의 표준편차는 0.145MW 이고, 대역폭이 10rad/s인 경우는 출력의 표준편차는 0.142MW이고, 대역폭이 13rad/s 이상인 경우는 출력의 표준편차는 0.141MW이다. 대역폭이 5rad/s이면 출력파워의 표준편차의 증가가 0.002MW 이내로 작고, 대역폭이 13rad/s 이상이면 출력파워의 표준편차의 증가가 없음을 확인할 수 있다.
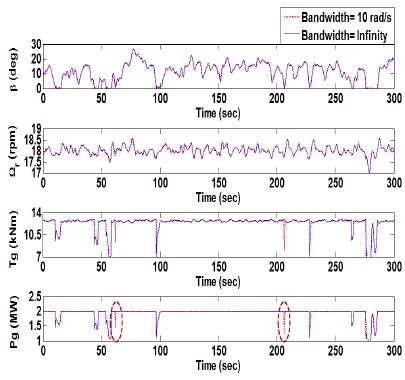
다음으로 피치 구동기의 대역폭이 파워딮에 미치는 영향을 살펴보자. Fig. 9와 Fig. 10은 각각 대역폭이 4rad/s와 10rad/s인 경우의 응답을 무한대인 경우의 응답과 비교하고 있다. 그리고 Fig. 11은 대역폭에 따른 출력파워의 응답을 비교하고 있다. 정격풍속 이상의 영역에서도 난류 풍속의 영향으로 인해 출력파워는 정격이하로 순간적으로 떨어지는 파워딮이 종종 발생하는데, 피치 구동기의 대역폭에 따른 파워딮의 차이는 61초, 151초, 206초 근처에서 발생함을 알 수 있다. 대역폭이 4rad/s에서는 61초, 151초, 206초 근처 모두에서 파워딮이 발생한다. 그러나 대역폭이 10 rad/s에서는 151초 근처에서 파워딮이 발생하지 않고, 61초와 206초 근처에서만 파워딮이 발생한다. 그리고 대역폭이 15rad/s 이상에서는 61초, 151초, 206초 근처 모두에서 파워딮이 발생하지 않음을 확인할 수 있다.
그러므로 출력파워의 평균, 표준편차, 파워딮 모두를 고려하면 피치 구동기의 대역폭이 15rad/s(피치 제어기의 대역폭의 15배) 이상이면 출력파워의 응답에 미치는 영향이 거의 없음을 알 수 있다.
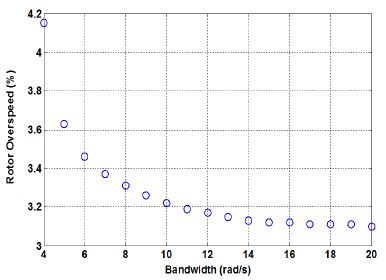
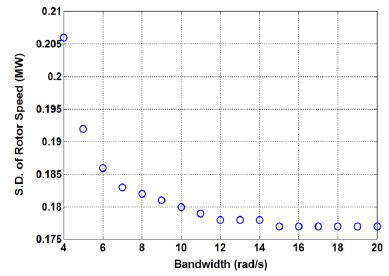
피치 구동기의 대역폭에 따른 로터속도의 평균, 표준편차, 과속을 살펴보자. 로터속도의 평균은 출력파워의 평균과 표준편차에서처럼 피치 구동기의 대역폭이 5rad/s 이상이면 대역폭의 영향이 매우 작음을 Table 2를 통하여 알 수 있다. 그러나 피치 구동기의 대역폭이 로터속도의 표준편차와 과속에 미치는 영향은 작지 않다. Fig. 12는 로터속도의 과속을 보여주고 Fig. 13은 로터속도의 표준편차를 보여준다.
로터속도의 과속의 경우 피치 구동기의 대역폭을 15rad/s 이상으로 크게 하여도 대역폭이 무한대인 경우(3.04%)와 같아지지는 않지만, 대역폭이 15rad/s 이상인 경우는 로터속도의 과속을 약 3.1% 정도로 줄일 수 있음을 확인할 수 있다. 그리고 대역폭이 15rad/s 이상이 되면 로터속도의 과속의 변화는 거의 없다. 대역폭이 4rad/s인 경우에는 로터속도의 최대값은 18.747rpm으로 과속이 4.15%로 크다. 대역폭이 10rad/s인 경우에는 로터속도의 최대값은 18.578 rpm으로 과속이 3.21%로 줄어든다. 그리고 대역폭이 15rad/s인 경우에는 로터속도의 최대값은 18.562rpm으로 과속이 3.12%로 줄어든다. 피치 구동기의 대역폭이 15rad/s 이상으로 커지면 대역폭이 4rad/s인 경우보다 로터속도의 과속을 1% 이상 줄일 수 있음을 알 수 있다.
로터속도의 표준편차의 경우도 피치 구동기의 대역폭을 15rad/s 이상으로 크게 하여도 대역폭이 무한대인 경우(0.174rpm)와 같아지지는 않지만, 대역폭이 15rad/s 이상인 경우는 로터속도의 표준편차를 0.177rpm까지 줄일 수 있음을 확인할 수 있다. 그리고 대역폭이 15rad/s 이상이 되면 로터속도의 표준편차의 변화는 거의 없다. 대역폭이 4rad/s인 경우는 로터속도의 표준편차가 0.206rpm이고, 대역폭이 10rad/s인 경우는 로터속도의 표준편차가 0.18rpm이고, 대역폭이 15rad/s인 경우는 로터속도의 표준편차가 0.177rpm이다. 피치 구동기의 대역폭이 15rad/s 이상으로 커지면 대역폭이 4rad/s인 경우보다 로터속도의 표준편차를 0.032rpm 정도로 줄일 수 있음을 알 수 있다.
그러므로 로터속도의 평균, 표준편차, 과속 모두를 고려하면 피치 구동기의 대역폭이 15rad/s(피치 제어기의 대역폭의 15배) 이상이면 로터속도의 응답에 미치는 영향이 매우 작음을 알 수 있다.
5. 결 론
본 논문에서는 풍력터빈의 피치 구동기의 대역폭이 출력파워와 로터속도의 응답에 미치는 영향에 대하여 정량적으로 살펴보고, 피치 구동기의 대역폭을 피치 제어기의 대역폭보다 어느 정도 크게 하는 것이 적절한가에 대하여 살펴보았다. 이를 위하여 2MW급 풍력터빈을 대상으로 IEC 규정의 Class A에 해당하는 난류풍속(평균풍속 16m/s, 난류강도 17.6%)을 이용하여 수치실험을 수행하여 풍력터빈의 응답을 정량적으로 살펴보았다. 피치 제어기의 대역폭은 1rad/s로 설정하였고, 이는 평균 출력파워의 강하가 0.4% 정도 이내에 해당함을 확인하였다.
피치 구동기의 대역폭이 출력파워의 평균과 표준편차에 미치는 영향은 매우 작음을 확인할 수 있었다. 평균 출력파워의 경우에는 대역폭이 5rad/s이면 감소율은 0.1% 이내로 매우 작았고, 대역폭이 15rad/s 이상이면 감소가 없음을 확인하였다. 출력파워의 표준편차의 경우에는 대역폭이 5rad/s이면 0.002MW 이내로 매우 작게 증가하였고, 대역폭이 13rad/s 이상이면 증가가 없었다. 그러나 피치 구동기의 대역폭이 출력파워의 파워딮에 미치는 영향은 15rad/s 미만까지는 있었지만 15rad/s 이상에서는 그 영향이 없음을 확인하였다.
피치 구동기의 대역폭이 로터속도의 평균에 미치는 영향은 대역폭이 5rad/s에서는 매우 작았고 15rad/s 이상이면 대역폭의 영향이 없음을 확인하였다. 그러나 피치 구동기의 대역폭이 로터속도의 표준편차와 과속에 미치는 영향은 작지 않음을 확인할 수 있었다. 대역폭이 15rad/s 이상에서는 로터속도의 과속과 표준편차의 변화는 거의 없었고, 대역폭이 무한대인 경우와 같아지지는 않고 약간의 차이가 발생하였다. 대역폭이 15rad/s 이상으로 커지면 대역폭이 4rad/s인 경우보다 로터속도의 과속은 1% 이상 줄일 수 있었고, 로터속도의 표준편차는 0.032rpm 정도로 줄일 수 있음을 확인할 수 있었다.
그러므로 본 연구의 정량적인 분석을 통하여 피치 구동기의 대역폭이 출력파워의 평균, 표준편차, 파워딮과 로터속도의 평균, 표준편차, 과속 모두의 응답에 미치는 영향을 최소화하기 위해서는 피치 구동기의 대역폭을 약 15rad/s 이상으로 설정하는 것이 바람직함을 확인할 수 있었다.
Nomenclature
| Bsq : | equivalent damping, kgm2/s |
| Cp,max : | maximum power coefficient |
| Gpa(s) : | transfer function of pitch actuator |
| Jr : | rotor’s mass moment of inertia, kgm2 |
| Jg : | generator’s mass moment of inertia, kgm2 |
| Jeq : | equivalent mass moment of inertia, kgm2 |
| Kopt : | optimal model gain |
| Ngb : | gearbox ratio |
| Nβg : | nonlinear parameter for pitch angle, Nm/deg |
| Pg : | power output, W |
| R : | rotor radius, m |
| Tr : | aerodynamic torque, Nm |
| Tg : | generator torque, Nm |
| V : | wind speed, m/s |
| Ωg : | generator speed, rad/s |
| Ωr : | rotor speed, rad/s |
| ρ : | air density, kg/m3 |
| β : | pitch angle, deg |
| λ : | tip speed ratio |
| λopt : | optimal tip speed ratio |
| ωBW : | bandwidth of pitch actuator, rad/s |
Acknowledgments
이 논문은 한밭대학교의 ERG에 의해 수행된 연구결과입니다.
References
- Hansen, A. D., Hansen, L. H., (2007), “Wind turbine concept market penetration over 10 years”, Wind Energy, Vol. 10(No. 1), p81-97.
- Joselin Herberta, G. M., Lniyanb, S., Sreevalsanc, E., Rajapandian, S., (2007), “A review of wind energy technologies”, Renewable and Sustainable Energy Review, Vol. 11, p1117-1145.
-
Burton, T., Sharpe, D., Jenkins, N., Bossanyi, E., (2001), “Wind energy handbook”, John Wiley & Sons.
[https://doi.org/10.1002/9781119992714]

- Bianchi, F. D., Battista, H. D., Mantz, R. J., (2007), “Wind turbine control systems: principles, modelling and gain scheduling design”, Springer-Verlag.
- Munteanu, I., Bratcu, A. L., Cutululis, N. A., Ceanga, E., (2008), “Optimal Control of Wind Energy Systems”, Springer-Verlag.
- Nam, Y. S., (2009), “Wind turbine control”, GS-Intervision.
- Lim, C. W., (2011), “Study on properties of pitch control for wind turbine”, Transaction of Korean Society of Mechanical Engineers(A), Vol. 35(No. 1), p59-65.
-
Leithead, W. E., Connor, B., (2000), “Control of variable speed wind turbines: dynamic model”, International Journal of Control, Vol. 73, p1173-1188.
[https://doi.org/10.1080/002071700417830]

-
Bianchi, F. D., Mantz, R. J., Christiansen, C. F., (2005), “Gain scheduling control of variable-speed wind energy conversion systems using quasi-LPV models”, Control Engineering Practice, Vol. 13, p247-255.
[https://doi.org/10.1016/j.conengprac.2004.03.006]

-
Munteanu, I., Cutululis, N. A., Bratcu, A. I., Ceangă, E., (2005), “Optimization of variable speed wind power systems based on a LQG approach”, Control Engineering Practice, Vol. 13, p903-912.
[https://doi.org/10.1016/j.conengprac.2004.10.013]

-
Jo, M. J., Park, S. G., (2015), “Design of control algorithm for floating offshore wind turbines”, New & Renewable Energy, Vol. 11, p3-11.
[https://doi.org/10.7849/ksnre.2015.06.11.2.3]

-
Tai, F. Z., Kang, K. W., Lee, J. H., (2011), “Study on the aerodynamics and control characteristics of 5 MW wind turbine”, New & Renewable Energy, Vol. 7, p59-69.
[https://doi.org/10.7849/ksnre.2011.7.2.059]

- Bossanyi, E. A., (2009), “GH Bladed version 3.82 user manual”, Garrad Hassan and Partners Ltd.
- ICE, “International Standard”, IEC 61400-1:2005(E), 2005-08.
-
Lim, C. W., (2016), “Design of a small-scale motor-generator system for a large wind turbine”, The KSFM Journal of Fluid Machinery, Vol. 20(No. 1), p48-52.
[https://doi.org/10.5293/kfma.2017.20.1.048]

-
Lim, C. W., (2017), “Design and manufacture of smallscale wind turbine simulator to emulate torque response of MW wind turbine”, International Journal of Precision Engineering and Manufacturing-Green Technology, Vol. 4(No. 4), p409-418.
[https://doi.org/10.1007/s40684-017-0046-6]

- Cho, J. H., (2012), “The effects of torque schedule and pitch loop bandwidth change on the performance & mechanical load of MW wind turbine”, Master Thesis, Kangwon University.