퍼지 TOPSIS를 이용한 에너지 선택 우선순위 결정

1. 서 론

한국은 에너지 다소비 산업인 제조업 중심의 산업구조와 화석연료 중심의 에너지 소비구조이고, 온실가스 의무감축 대상국(제1차 기후변화대응 기본계획에서 2030년까지 배출전망치 대비 37%의 온실가스 감축)이기 때문에, 신재생 에너지 보급 확대는 선택이 아니라 필연적 정책과제가 되었다. 특히 발전 측면에서 신재생에너지 비중확대와 석탄화력의 비중축소(제7차 전력수급기본계획에서 석탄화력 신규 4기 취소 및 미세먼지 특별대책에 따른 노후 10기 폐지) 계획을 기초로 해서, 에너지 자립을 위해서는 공급 변동성이 큰 신재생에너지와 기존 화석 에너지를 효율적으로 혼합하는 에너지 믹스 정책이 수립되어야 한다. 최근 전력에너지 수급에서 발전량 비중은 발전단가가 저렴한 원자력과 태양광, 풍력, 조력 등 신재생 에너지들은 점진적으로 증가 추세이나, 석탄, 석유, LNG 등 기존 화석 에너지들은 감소 추세이다. 이와 같은 다양한 에너지들의 선택문제는 제약된 정부예산에서 에너지를 효율적으로 공급하기 위해서 여러 가지 에너지 선택기준의 속성들을 고려해야 하는 중요한 다기준(혹은 다속성) 의사결정문제이다. 그러나 다양한 속성들을 고려해야 하는 에너지 정책 전문가들은 아직도 과거 에너지 정책에 대한 자료와 직관에 의해서 에너지 선택에 대한 우선순위를 결정하고 있다. 이와 같은 에너지 정책 전문가들의 주관적인 판단은 애매모호하기 때문에, 정확한 계량적 수치로 이를 정확하게 측정한다는 것은 실제로는 대부분 불가능하다. 그러므로 주관적인 선호 정도를 정확하게 수치로 측정하는 것보다는 언어적 변수(linguistic variable)로 측정하는 것이 훨씬 더 실용적인 추정방법이라고 할 수 있다. 이러한 주관적인 모호성(ambiguity)을 동반하는 우선순위 의결정문제를 해결할 수 있는 접근방법이 바로 Zadeh (1965)^[1]의 퍼지 집합이론이다. 다기준 의사결정문제(MCDM: Multi-Criteria Decision Making)를 해결하는 방법 중 하나인 TOPSIS (Technique for Order Performance by Similarity to Ideal Solution)는 긍정적인 해(PIS: Positive Ideal Solution)로부터는 가장 가까운 거리에 있고, 부정적인 해(NIS: Negative Ideal Slution)로부터는 가장 먼 거리에 있는 대체안을 최종 선택하는 방법이다. 본 연구에서는 집단적인 의사결정의 대체안들과 의사결정기준의 가중치를 언어적 변수로 측정되는 퍼지 자료로 측정했다. 그리고 TOPSIS 방법을 이용해서, 퍼지 긍정적인 해(FPIS: Fuzzy Positive Ideal Solution)와 퍼지 부정적인 해(FNIS: Fuzzy Negative Ideal Solution)를 정의했고, FPIS와 FNIS로부터 대체안의 거리는 vertex 방법을 이용해서 계산했다. 그리고 대체안의 근접계수 값은 클수록 FPIS로 부터는 더 가깝고, FNIS로 부터는 더 멀기 때문에, 대체안들의 근접계수(CC: Closeness Coefficient)를 계산한 후에, 대체안들의 우선순위를 최종적으로 결정했다.

연구목적은 첫째, 의사결정기준에 대한 가중치와 대체안에 대한 성과 측정치에 대한 에너지 정책 전문가들의 주관적으로 모호한 판단을 언어적 변수인 삼각형 퍼지 수로 변환시키는 퍼지 집합방법을 제시한다. 둘째, 7개의 의사결정기준에서 실행 가능한 10개의 에너지 대체안들을 평가해서 최적 에너지 선택에 대한 우선순위를 결정하는 다기준 의사결정문제에 퍼지 TOPSIS 방법 적용절차를 제시한다. 셋째, 경제적 관점이외에 기술, 사회, 환경 등 다기준 관점에서 최적 에너지 선택 우선순위에 기초해서 녹색 에너지 정책 수립을 위한 접근방법을 제시한다. 본 논문 2장에서는 에너지 선택을 위한 다기준 의사결정모형과 의사결정기준에 관한 기존 연구를 기술했고, 3장에서는 퍼지 TOPSIS 방법을 기술했다. 4장에서는 전력 에너지 선택에 관한 다기준 의사결정사례에 퍼지 TOPSIS 방법을 적용해서 에너지 정책수립을 위한 에너지 선택의 우선순위방법을 제시했고, 마지막 5장에서는 연구의 결론과 한계점을 기술했다.

2. 기존연구

2.2 에너지 선택기준

에너지의 종류는 석탄과 석유와 같이 CO₂를 발생시키는 화석 에너지, 그리고 지속가능한 신재생 에너지로 구분된다. 신에너지 및 재생에너지의 개발･이용･보급 촉진법에서 신재생에너지는 ‘기존의 화석연료를 변환시켜 이용하거나 햇빛, 물, 지열, 강수, 생물유기체 등을 포함하여 재생 가능한 에너지를 변환시켜 이용하는 에너지’로 정의하고 있다, 여기서 신에너지는 기존 화석연료를 친환경적으로 변환하여 에너지를 생산하는 수소에너지, 연료전지, 석탄액화 및 가스화 등 3개 분야를 의미하고, 재생 에너지는 재생 가능한 에너지를 활용하여 에너지를 생산하는 태양광, 태양열, 바이오, 풍력, 수력, 지열, 해양, 폐기물 등 8개 분야를 의미한다. 또한, 한국산업기술평가원(KEIT)의 산업기술 분류표에서는 에너지･자원 분야 중 신재생에너지 기술을 태양열, 태양광, 바이오연료, 폐기물, 소수력, 풍력, 해양, 지열, 수소, 연료전지, 석탄가스/액화, 합성연료 등으로 구분했다. Baños et al.(2011)^[14]는 지속가능한 재생 에너지들을 풍력, 태양 에너지, 수력, 바이오 에너지, 지열 에너지, 혼합 시스템 등으로 분류했다. 본 연구에서는 에너지의 종류를 우리나라의 전력 상황을 고려해서, 기존 핵심 에너지인 원자력, 석탄, 석유, LNG, 수력 이외에, 태양광, 풍력, 조력, 바이오, 폐기물가스화 등 모두 10개로 구분했다.

에너지의 선택기준에 대해서 Beccali et al.(2003)^[15]는 재생 에너지 기술 확산에 대한 실행계획을 기술적, 환경적, 사회경제적 의사결정기준 관점에서 Electre III 방법으로 평가했다. 이와 유사한 에너지 의사결정기준에 관한 연구들이 최근까지 기술적, 경제적, 환경적, 사회정치적, 등 4가지 관점에서 연구되었으며, 종합적으로 Wang et al.(2009)^[16]이 지속가능 에너지에 대한 다기준 의사결정 관련 최근 논문 33편을 분석해서 기술적, 경제적, 환경적, 사회적 등 4개 관점에서 Table 1 과 같이 기존 연구의 선택기준들을 정리했다.

Kahraman과 Kaya(2010)^[17]는 Wang et al.(2009)^[16]의 연구를 기초로 해서, 9개의 에너지(석탄, 석유, 원자력, 태양광, 풍력, 수력, 바이오매스, 천연가스, 지열)에 대해서 기술적(타당성, 위험, 신뢰성, 준비단계기간, 실행단계기간, 연속성 및 성과 예측성, 기술적 노하우), 경제적(실행비용, 자금의 유용성, B/C, IRR 등 경제적 가치), 환경적(공해 방출, 토지사용, 폐기물 처리 필요성), 사회･정치적(국가 에너지 목표와의 일관성, 정치적 수용성, 사회적 수용성, 노동력에 대한 영향) 에너지 선택기준 17개를 적용했다. 또한, Kaya와 Kahraman(2011)^[10]은 Wang et al.(2009)^[16]의 연구를 근거로 7개의 에너지(석탄/석유, 원자력, 태양광, 풍력, 수력, 바이오매스, 열병합)에 대해서 기술적(효율성, 에너지 효율성), 경제적(투자비용, 운영 및 유지비용), 환경적(NO_x 방출, CO₂ 방출, 토지사용), 사회적(사회적 수용성, 직업창출) 에너지 선택기준 9개를 적용했다.

Table 1.

Decision criteria for energy selection

본 연구에서는 Kaya와 Kahraman(2011)^[10]이 제시했던 9개의 선택기준들 중에서, 사례연구를 위한 7명의 에너지 전문가집단의 표적집단면접(FGI: Focus Group Interview)을 통해서, 에너지 효율성 대신에 안전성이 선택되었고, NO_x 방출과 CO₂ 방출은 합쳐서 공해배출로 표현했으며, 직업창출은 제외시켰고, 최종적으로 적용 타당성이 높은 7개의 선택기준들(효율성, 안전성, 투자비용, 운영비용, 공해배출, 토지사용, 사회적 수용성)이 도출되었다. 또한, 본 연구에서는 Kaya와 Kahraman(2011)^[10]이 제시했던 7개 선택기준들 중에서 7명의 에너지 정책전문가 집단의 표적집단면접을 통해서, 석탄/석유는 2개의 에너지 대체안으로 분리시키고, 이외에 조력과 폐기물가스화를 추가시켜서 10개의 에너지 대체안들(태양광, 원자력, 풍력, 조력, 페기물가스화, 바이오, 수력, 석탄, 석유, LNG)을 도출했다.

3. 에너지 선택을 위한 퍼지 TOPSIS 방법

전통적 집합(classical set or crisp set)은 셀 수 있는 요소들의 모임이지만, 퍼지 집합은 소속 함수(membership function)를 통해 요소들을 표현한다. 퍼지 집합이론의 퍼지 논리에 의하면, X 전체집합 내의 퍼지 집합 $$ \tilde{a}$$는 X의 각 원소 x가 구간 [0,1] 내의 어떤 실수와 관련된 하나의 소속함수 $$ {\mu }_{\tilde{a}}$$(x)로서 나타낸다. 함수 값 $$ {\mu }_{\tilde{a}}$$(x)는 $$ \tilde{a}$$ 내에 x의 소속 정도를 표현한다. 또한, X 전체집합 내의 퍼지 집합 $$ \tilde{a}$$ 가 ∃x_i∈X, $$ {\mu }_{\tilde{a}}\left(x\right)$$ = 1 라면, 정규화 된 퍼지 집합이라고 부른다.^[18] 어떤 삼각형 퍼지 수 $$ \tilde{a}$$ 는(a₁,b₂,c₃)로 정의할 수 있다. 퍼지 수 $$ \tilde{a}$$ 의 소속 함수 $$ {\mu }_{\tilde{a}}$$(x)는 다음과 같다.^[19]

어떤 두 개의 삼각형 퍼지 수의 덧셈과 뺄셈의 결과도 역시 삼각형 퍼지 수이지만, 곱셈의 결과는 근사한(approximate) 삼각형 퍼지 수가 된다. 두 개의 삼각형 퍼지 수인 $$ \tilde{a}$$=(a₁,a₂,a₃)과 $$ \tilde{b}$$(b₁,b₂,b₃)이 주어졌다면, 두 개 퍼지 수의 산술계산은 다음과 같다.^[20]

의사결정자가 선택해야 하는 m개의 대체안과 n개의 의사결정기준 그리고 K 명의 의사결정자의 퍼지 다기준 의사결정문제는 다음과 같다.

Fig. 1.

Triangular fuzzy number ã

$$ D=\begin{array}{ccc}\begin{array}{cc}\begin{array}{c}\hfill \\ A_1\hfill \\ A_2\hfill \end{array}\hfill & \begin{array}{c}{C}_1\hfill \\ {\tilde{x}}_{11}\hfill \\ {\tilde{x}}_{21}\hfill \end{array}\hfill \end{array}\hfill & \begin{array}{cc}\begin{array}{c}{C}_2\hfill \\ {\tilde{x}}_{12}\hfill \\ {\tilde{x}}_{22}\hfill \end{array}\hfill & \begin{array}{c}\hfill \\ \cdots \hfill \\ \cdots \hfill \end{array}\hfill \end{array}\hfill & \begin{array}{c}{C}_n\hfill \\ {\tilde{x}}_{1n}\hfill \\ {\tilde{x}}_{2n}\hfill \end{array}\hfill \\ \begin{array}{cc}:\hfill & :\hfill \end{array}\hfill & \begin{array}{cc}:\hfill & :\hfill \end{array}\hfill & :\hfill \\ \begin{array}{cc}{A}_m\hfill & {\tilde{x}}_{m1}\hfill \end{array}\hfill & \begin{array}{cc}{\tilde{x}}_{m2}\hfill & \cdots \hfill \end{array}\hfill & {\tilde{x}}_{mm}\hfill \end{array}$$

W = [w₁,w₂,… w_n]

여기서 i=1,…,m, j=1,…,n, A₁,A₂,…,A_m은 선택해야할 대체안들이고 C₁,C₂,…,C_n은 의사결정기준이며, w_j는 의사결정자의 각 의사결정기준에 대한 가중치이다.

Chen(2000)^[21]은 Hwang과 Yoon(1981)^[22]이 도출한 TOPSIS 방법을 기반으로 삼각형 퍼지 수를 가정한 후에, 두 퍼지 수의 거리를 유클리드 거리(Euclidean distance)로 계산하는 확장된 퍼지 TOPSIS 방법을 제시했다. 여기서 의사결정기준들의 중요성을 측정하고, 의사결정기준 관점에서 대체안들을 언어적 변수로 평가했다. 퍼지 다기준 의사결정문제의 퍼지 자료에 대해서 TOPSIS 방법을 적용시키는 7 단계 별 적용절차는 다음과 같다.

단계 1: 의사결정기준에 대한 가중치를 도출한다. 퍼지 다기준 의사결정문제에서 의사결정기준 C_j에 대한 가중치 $$ {\tilde{w}}_j$$는 양의 삼각형 퍼지 수로 측정 가능하다고 가정한다.^[21]

단계 2: 대체안에 대한 의사결정자들의 평가 결과인 퍼지 의사결정행렬을 도출한다. 퍼지 다기준 의사결정문제(FMCDM)에서 성과측정치 $$ {\tilde{x}}_{ij}$$는 양의 삼각형 퍼지 수로 측정 가능하다고 가정한다. 여기서 $$ {\tilde{x}}_{ij}$$는 K명의 의사결정자의 의사결정기준 C_j 관점에서 대체안 A_i를 평가한 성과측정치 x_ij를 총합하는데는 산술평균을 사용한다.^[21]

단계 3: 다기준 의사결정문제에서 서로 다른 척도로 평가된 측정값들을 정규화 한다. 선형척도변환을 이용해서 서로 다른 의사결정기준의 척도를 비교가능한 척도로 변환시킨다. 의사결정기준은 측정치가 클수록 선호되는 이득기준과 측정치가 작을수록 선호되는 비용기준으로 구분된다. 정규화 퍼지 의사결정 행렬은 다음과 같다.^[20]

여기서 B와 C는 각각 이득기준과 비용기준의 집합이다.

$$ \begin{array}{cc}{c}_j^{*}=\max c_{ij},& j\in B,\\ c_j^{-}=\min c_{ij},& j\in C,\end{array}$$

이와 같은 정규화 방법은 요소 $$ \tilde{r}$$, ∀i,j 의 표준화 된 삼각형 퍼지 수가 [0, 1]에 속하는 성질이 유지된다.

단계 4: 각 의사결정기준에 대해서 서로 다른 가중치가 할당된 정규화 된 퍼지 의사결정 행렬 $$ \tilde{V}$$ 는 다음과 같다.^[21]

여기서 $$ \widetilde{v_{ij}}=\widetilde{r_{ij}}⨂\widetilde{w_j}$$, 그리고 i=1,2,…,m. j=1,2,…,n. 이다. $$ {\tilde{w}}_j$$는 기준 C_j에 대한 중요도를 나타내는 가중치이다.

단계 5: 가중치가 부여된 정규화 된 퍼지 의사결정 행렬 $$ \tilde{V}$$에 따라서, 정규화 된 양의 삼각형 퍼지 수의 요소 $$ {\tilde{v}}_{ij}$$, ∀i,j 를 계산 할 수 있다. 퍼지 긍정적인 해(FPIS A^*)와 퍼지 부정적인 해(FNIS A^-)는 다음과 같다.^[21]

여기서 $$ {\tilde{v}}_j^{*}=\left(\mathrm{1,1},1\right), {\tilde{v}}_j^{-}=\left(\mathrm{0,0},0\right)$$ 그리고 j=1,2,…,n. 이다.

단계 6: n차원의 유클리디안 거리를 이용해서 각 대체안들에 대한 FPIS A^*와 FNIS A^-로부터의 거리는 다음과 같이 계산한다.^[21]

여기서 d_v(.,.)는 두 퍼지 수들 간의 거리 측정치, 그리고 i=1,2,…,m. j=1,2,…,n. 이다. $$ d_i^{*}$$는 FPIS A⁺로부터 각 대체안 A_i로부터의 거리이고, $$ d_i^{-}$$는 FNIS A^-로부터 각 대체안 A_i로부터의 거리이다. 두 개의 삼각형 퍼지 수 $$ \tilde{m}$$=(m₁,m₂,m₃)와 $$ \tilde{n}$$=(n₁,n₂,n₃) 간의 거리는 vertex 방법을 이용해서 계산한다.^[20]

단계 7: 모든 의사결정 대체안들의 우선순위를 최종적으로 확정하기 위해서, 각 대체안들의 상대적 근접도 계수 CC를 계산한다.^[21]

만약 A_i=A^*이면 CC_i=1이고, A_i=A^-이면 CC_i=0 이다. 여기서 CC_i값이 1에 가까울수록 대체안이 FPIS A⁺에 더 가까워지고, FNIS A^-에서는 더 멀어진다. CC_i 값이 클수록 대체안 A_i의 좋은 성과를 의미하므로, 모든 대체안들의 우선순위를 결정할 수 있고, 또한 실행 가능한 대체안들 중에서 최적 대체안을 선택할 수 있다.

4. 사례연구

4.1 에너지 선택 사례 개요

사례연구를 위한 에너지 전문가집단은 과거 에너지 관련 논문 혹은 프로젝트 경험이 있는 에너지 정책수립 전문가들로 구성되었으며, 사례연구는 표적집단면접과 설문지 조사에 의해서 실행되었다. 7명의 에너지 정책수립 전문가들, 구체적으로 대학교수 3명(경영학전공 1명, 산업공학전공 2명), 한국전기연구원 연구원 1명(전기공학전공), 한국개발연구원 연구원 1명(경제학전공), 한국전력공사 팀장 1명(전기공학전공), 한국수력원자력(주) 팀장 1명(전기공학전공)이 10개의 에너지 대체안들을 평가했다. 의사결정기준은 네 가지 평가(기술적, 경제적, 환경적, 사회적) 관점에서 7개의 평가기준을 적용하고자 한다. 본 연구의 에너지 의사결정문제는 Fig. 2 와 같이, 7개의 의사결정기준은 효율성(C₁), 안전성(C₂), 투자비용(C₃), 운영비용(C₄), 공해배출(C₅), 토지사용(C₆), 사회적 수용성(C₇) 이고, 10개의 대체안은 태양광(A₁), 원자력(A₂), 풍력(A₃), 조력(A₄), 폐기물가스화(A₅), 바이오(A₆), 수력(A₇), 석탄(A₈), 석유(A₉), LNG(A₁₀) 이다. 의사결정기준에서 기술적 관점에서 에너지 효율성과 안전성, 경제적 관점에서 투자비용, 운영 및 유지비용, 연료비용, 환경적 관점에서 공해배출과 토지사용, 사회적 관점에서 사회적 수용성이며, 각 용어에 대한 개념은 다음과 같다.

Fig. 2.

Hierarchical structure of decision problem

효율성(C₁): 에너지 원천으로부터 얼마나 많이 이용 가능한 에너지를 얻을 수 있는 정도로 측정한다. 가장 자주 이용되는 효율성 척도인 효율성 계수는 입력 에너지와 출력 에너지의 비율로 정의된다. 이것은 에너지 시스템을 평가하는 기술적 기준으로 가장 많이 사용된다.

안전성(C₂): 에너지 기술에 대한 위험이 존재하므로, 에너지 시스템에 대한 안전성의 정도를 평가해야 한다.

투자비용(C₃): 투자비용에는 기계 장비 및 설비의 구입비, 전국망을 연결시키는 구축비, 엔지니어링 서비스, 토지구입비용을 제외한 기타 건축비 등이 포함된다. 투자비용은 에너지 시스템을 평가하는데 가장 자주 사용되는 경제적 기준이며, 이와 동시에 이득도 평가된다.

운영비용(C₄): 운영비용은 에너지를 발생시키는데 소요되는 비용, 임금 등 이고, 또한 설비를 유지보수 하는 유지비용도 포함된다.

공해배출(C₅): 화석연료 의존이 높은 에너지 시스템에서 주로 배출되는 공해는 CO₂를 포함한 온실가스, 액체 및 고체 폐기물, 전자파, 악취 등이다. 이러한 공해배출 기준에 대한 평가에서는 배출 형태와 배출량, 그리고 처리비용 등이 고려되어야 한다. 특히 온실가스에 의한 지구온난화 문제를 해결하기 위해서 온실가스 감축방안이 추진 중이다.

토지사용(C₆): 모든 에너지 시스템이 자연환경에 직접적으로 영향을 주므로, 설치장소에 소요되는 토지의 면적과 가격은 중요한 평가요소가 된다.

사회적 수용성(C₇): 사회적 수용성은 에너지 시스템에 대한 지역주민들의 긍정적인 의견수렴 정도를 의미한다. 지역주민들과 관련된 이해관계자들의 의견이 에너지 프로젝트를 실행하는데 큰 영향력을 행사하기 때문에 중요하게 고려해야 할 평가 요소이다.

본 연구의 에너지 관련 다기준 의사결정문제의 평가기준에 대한 객관적인 측정 자료를 한국전력 등 에너지 관련기관으로부터는 구할 수 없기 때문에, 현실적으로 에너지 정책 전문가들은 과거 프로젝트 경험을 근거로 주관적 추정치로 평가할 수밖에 없는 상황이다. 그러므로 7개의 의사결정기준과 10개의 에너지 대체안들에 대한 주관적 가중치를 도출하기 위해서 다음과 같은 퍼지 TOPSIS 방법을 적용했다.

4.2 퍼지 TOPSIS 방법의 적용

본 연구에서 퍼지 TOPSIS 방법의 7 단계 적용절차는 다음과 같다.

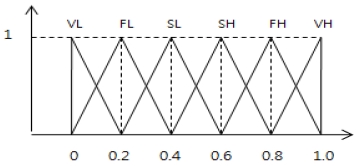
단계 1: 의사결정기준에 대한 가중치를 도출하기 위해서, 가중치는 Fig. 1 과 같은 양의 삼각형 퍼지 수로 측정 가능하다고 가정한다. 7개의 의사결정기준인 효율성(C₁), 안전성(C₂), 투자비용(C₃), 운영비용(C₄), 공해배출(C₅), 토지사용(C₆), 사회적 수용성(C₇)에 대해 Table 2 와 같은 서로 다른 6개의 언어적 척도(VL; Very Low, FL; Fairly Low, SL; Slightly Low, SH; Slightly High, FH; Fairly High, VH; Very High)로 평가한다.^[23]

Table 2.

The linguistic terms and related fuzzy numbers of evaluation ratings and criteria weights

7 명의 의사결정자(D₁~D₇)가 7개의 의사결정기준(C₁~C₇) 에 대해서 Table 2 와 같은 언어적 척도로 평가한 결과가 Table 3 이다. 그리고 산술평균 $$ {\tilde{x}}_{ij}$$를 사용해서 총합한 결과가 Table 4 이다. 예로써, Table 3 에서 효율성(C₁)에 대한 7명의 의사결정자들의 평가는 SH, SH, SH, SH, FH, VH, SH 이다. 이를 Table 2 의 삼각형 퍼지 수로 변환시킨 후에, 산술평균을 계산하면, (0.49, 0.69, 0.86)이 도출된다. 여기서 삼각형 퍼지 수를 defuzzify 해서 BNP(best nonfuzzy performance) 값을 구하기 위해서 산술평균하는 COA(center of area) 방법은 Zhao와 Govind(1991)^[24]가 이용했었다. 예로써, 효율성(C₁)의 가중치 (L_w1,M_w1,U_w1)에 대한 BNP 값은 다음과 같이 계산된다.

$\[ \begin{array}{c}{BNP}_{w_1}=\left[\left(U_{w_1}-L_{w_1}\right)+\left(M_{w_1}-L_{w_1}\right)/3+L_{w_1}\right]\hfill \\ =\left[\left(0.86-0.49\right)+\left(0.69-0.49\right)\right]/3+0.49\hfill \\ =0.68\hfill \end{array} \]$

(16)

Table 3.

The linguistic ratings evaluated by decisionmakers

Table 4.

The BNP value of a fuzzy number

단계 2: 의사결정대안에 대한 의사결정자들의 평가 결과인 퍼지 의사결정행렬을 도출하기 위해서, Fig. 3과 같은 양의 삼각형 퍼지 수로 측정 가능하다고 가정한다. 10개의 의사결정대안인 태양광(A₁), 원자력(A₂), 풍력(A₃), 조력(A₄), 폐기물가스화(A₅), 바이오(A₆), 수력(A₇), 석탄(A₈), 석유(A₉), LNG(A₁₀)에 대해 Table 2 와 같은 서로 다른 6개의 언어적 척도(VL, FL, SL, SH, FH, VH)로 평가한 것이 Table 5 이다. 여기서 의사결정기준 C₁~C₇ 관점에서 대안 A₁~A₁₀를 평가한 7명의 의사결정자가의 성과측정치 xij를 산술평균한 결과가 Table 6 이다.

Fig. 3.

Membership function for linguistic value and criteria weights

Table 5.

Ratings of the 10 alternatives by 7 decisionmakers under 7 decision criteria

Table 6.

Fuzzy group decision matrix and fuzzy weights of 7 decision criteria

예로써, Table 5 에서 효율성(C₁) 관점에서 태양광(A1)에 대한 7명의 평가는 FL, SL, FL, FL, SL, FL, FL 이다. FL = (0.0, 0.2, 0.4), SL = (0.2, 0.4, 0.6)를 삼각형 퍼지수로 변환해서, 각 요소 별로 산술평균한 것이 대체안들에 대한 의사결정행렬 Table 6 에서 효율성(C₁) 관점에서 태양광(A1)에 대한 퍼지가중치 (0.06, 0.20, 0.40) 이다.

단계 3: 식 (7)을 이용해서 계산한 정규화 행렬 $$ {\tilde{R}=\left[{\tilde{r}}_{ij}\right]}_{m\times n}$$이 정규화 의사결정행렬 Table 7 이다. 대체안들에 대한 의사결정행렬 Table 6 에서 이득기준으로 측정된 C₁~C₂에 대해서 $$ c_1^{*}$$= 0.97, $$ c_2^{*}$$= 1.00 이므로 식(8)을 이용하고, 손실기준으로 측정된 C₃~C₇에 대해서 $$ c_3^{-}$$= 0.17, $$ c_4^{-}$$= 0.11, $$ c_5^{-}$$= 0.03, $$ c_6^{-}$$= 0.23, $$ c_7^{-}$$= 0.06 이므로 식(9)를 이용해서 계산한다.

Table 7.

Normalized group decision matrix

단계 4: 각 의사결정기준에 대해서 서로 다른 가중치가 할당된 정규화 퍼지 의사결정 행렬 $$ \tilde{V}$$ 을 계산한다. $$ {\tilde{v}}_{ij}={\tilde{r}}_{ij}\otimes {\tilde{w}}_j$$를 이용해서 계산한 정규화 퍼지 행렬 $$ \tilde{V}={\left[{\tilde{v}}_{ij}\right]}_{m\times n}$$ 이 가중치가 부여된 정규화 의사결정행렬 Table 8 이다. 예로써, 가중치가 부여된 정규화 의사결정행렬 Table 8 에서 효율성(C₁) 관점에서 태양광(A₁)에 대한 가중치가 부여된 정규화 퍼지 가중치 (0.03, 0.14, 0.35)는 정규화 의사결정행렬 Table 7 의 효율성(C₁) 관점에서 태양광(A₁)의 정규화 값 (0.06, 0.21, 0.41)에 대체안들에 대한 의사결정행렬 Table 6 의 효율성(C₁)의 가중치(0.49, 0.69, 0.86)의 곱으로 계산된 것이다.

Table 8.

Weighted normalized group decision matrix

단계 5: 양의 삼각형 퍼지 수는 구간 [0, 1] 내에 존재하기 때문에, 퍼지 긍정적인 해(FPIS, A^*)과 퍼지 부정적인 해(FNIS, A^-)는 각 행별로 최대값과 최소값으로 다음과 같다.

$\[ A^{*}=\left[\left(\mathrm{0.86,0.86,0.86}\right),\left(\mathrm{1.00,1.00.1}.00\right),\left(\mathrm{0.94,0.94,0.94}\right),\left(\mathrm{0.91,0.91,0.91}\right),\left(\mathrm{0.94,0.94,0.94}\right),\left(\mathrm{0.63,0.63,0.63}\right),\left(\mathrm{0.91,0.91,0.91}\right)\right] \]$

(17)

$\[ A^{-}=\left[\left(\mathrm{0.03,0.03,0.03}\right),\left(\mathrm{0.08,0.08,0.08}\right),\left(\mathrm{0.11,0.11,0.11}\right),\left(\mathrm{0.07.0}.07.0.07\right),\left(\mathrm{0.02,0.02,0.02}\right),\left(\mathrm{0.06,0.06,0.06}\right),\left(\mathrm{0.03,0.03,0.03}\right)\right] \]$

(18)

단계 6: 각 대안에 대한 퍼지 긍정적인 해(FPIS, A^*)과 퍼지 부정적인 해(FNIS, A^-)로 부터의 거리인 $$ d_i^{*}$$과 $$ d_j^{-}$$을 계산한 것이 Table 9 와 Table 10 이다. 예로써, Table 9에서 태양광(A₁)에 대한 퍼지 긍정적인 해로 부터의 거리 $$ d_i^{*}$$는 다음과 같이 계산된다.

$\[ d_1^{+}=\sqrt{1/3\left[{\left(0.86-0.03\right)}^2+{\left(0.86-0.14\right)}^2+{\left(0.86-0.35\right)}^2\right]=0.698} \]$

(19)

Table 9.

Distance between Ai and A*

Table 10.

Distance between Ai and A-

단계 7: 각 대체안의 상대적 근접도계수 CC_i의 크기에 따라서 실행가능한 모든 대체안들의 우선순위를 결정한다. 식 (12)를 이용해서, 각 대체안에 대한 FPIS A⁺와, FNIS A^-으로 부터 거리 $$ d_i^{*}$$와 $$ d_j^{-}$$를 계산해서, 각 대체안의 상대적 근접도 계수 CC_i를 도출한 결과가 Table 11 이다. 예로써, 첫 번째 대체안(A₁)에 대한 근접도 계수 CC₁은 다음과 같이 계산한다.

$\[ \begin{array}{c}{CC}_1=d_1^{-}/\left(d_1^{*}+d_1^{-}\right)\hfill \\ =2.799/\left(4.026+2.799\right)=0.410\hfill \end{array} \]$

(20)

Table 11.

Computation of di*, di- and CCi

여기서 근접도 계수 CC_i 값이 클수록 대체안 Ai의 좋은 성과를 의미하기 때문에, Table 11 에서 대체안들의 우선순위는 근접도 계수 CC_i의 크기 순서에 따라서, 결론적으로 A₁≻A₃≻A₆≻A₇≻A₁₀≻A₄≻A₉≻A₅≻A₂≻A₈ 순으로 선호된다.

5. 결 론

본 연구는 에너지 정책수립에 경제적 요인 이외 어느 요인이 영향을 많이 미치는지 알아내기 위해서, 에너지 선택 의사결정을 단순히 경제적 관점이외에 기술, 사회, 환경 등 다기준 관점에서 10개의 발전 에너지 선택에 대한 우선순위를 결정하기 위해서 퍼지 TOPSIS 방법으로 분석했다. 연구결과를 요약하면 다음과 같다.

첫째, 전력 에너지 정책전문가들의 모호한 주관적 판단을 6가지의 언어적 척도(VL, FL, SL, SH, FH, VH)인 삼각형 퍼지 수로 나타내는 퍼지 집합이론으로 의사결정기준들과 대체안들을 평가하는 방법을 제시했다. 둘째, 7개의 의사결정기준에서 실행 가능한 10개의 에너지 대체안들을 평가하여 최적 에너지를 선택하는 다기준 의사결정문제에 퍼지 TOTSIS 방법의 적용 절차를 제시하였다. 셋째, 에너지 선택의 우선순위는 기술적(에너지 효율성, 안전성), 경제적(투자비용, 운영비용), 환경적(공해배출, 토지사용), 사회적(사회적 수용성) 등 다기준 관점에서 태양광(A₁) ≻ 풍력(A₃) ≻ 바이오(A₆) ≻ 수력(A₇) ≻ LNG(A₁₀) ≻ 조력(A₄) ≻ 석유(A₉) ≻ 폐기물가스화(A₅) ≻ 원자력(A₂) ≻ 석탄(A₈) 순으로 선호된다. 본 연구의 의의는 에너지 정책전문가들의 모호한 주관적 판단을 정확한 계량적 수치로 측정하기 어려울 때, 퍼지집합을 적용하는 것이 실무적으로 합리성이 있다는 것이다. 또한, 본 연구의 적용방법의 타당성은 긍정적인 해 FPIS와 부정정인 해 FNIS를 동시적으로 고려하는 TOPSIS 방법이 집단의사결정의 효율적인 접근방법으로 에너지 정책수립의 활용성을 제고시킨다는 것이다. 향후 급격한 기술혁신이 동반되지 않는 한 에너지 믹스 변화에 대한 상당한 비용부담이 뒤따르게 되므로, 신재생에너지의 다변화에 의한 에너지 믹스 전략은 기술, 경제, 환경, 사회 등 다기준 관점에서 발전 에너지 선택을 위한 우선순위를 고려해서 에너지 정책이 추진되어야 한다.

끝으로 본 연구에서 적용된 퍼지 TOPSIS 방법론은 민감도 분석 혹은 AHP 방법과 같은 일관성 지수를 도출 할 수 없다는 한계점이 있다. 그러므로 이러한 한계점을 보완하기 위해서 퍼지 TOPSIS 방법에서는 각 대체안의 근접도 계수 CC_i를 도출해서, 대체안들의 우선순위를 결정하였다. 본 연구에서 제시된 퍼지 TOPSIS 방법과 더불어서 발전단가 관련비용을 고려한 추가적인 연구가 이루어진다면, 실제 전력 에너지 전략수립에 실용적으로 활용되는 분석도구가 될 것이다.

Acknowledgments

본 연구는 2017년도 광운대학교 교내연구비 지원으로 수행되었습니다.

References

• Zadeh, L. A., (1965), “Fuzzy Sets”, Information Control, 8, p338-353.
• Belton, V., and T. J. Stewart, (2002), Multiple Criteria Decision Analysis: An Integrated Approach, Boston, Kluwer Academic Publications.
• Keeney, R. L., and H. Raiffa, (1976), Decision with Multiple Objectives: Preference and Value Trade Offs, John Wiley and Sons.
• 이성곤, Gento Mogi, 윤용진, 김종욱, “Fuzzy AHP 기법을 적용한 전략적 에너지기술정책 연구”, 한국신재생에너 지학회, 한국신재생에너지학회 학술대회논문집, (2007), 6, p742-746.
• 이성곤, Gento Mogi, 김종욱, “Fuzzy AHP기법을 적용한 에너지개발전략 우선순위 연구”, 한국신재생에너지학회, 신재생에너지, 4(1), (2008, Mar), p19-24.
• Huang, J.-P., K. L. Poh, and B. W. Ang, (1995), “Decision Analysis in Energy and Environment Modelling”, Energy, 20, p843-855.
• Zhou, P., B. W. Ang, and K. L. Poh, (2006), “Decision Analysis in Energy and Environmental Modelling; An Update”, Energy, 31, p2604-2622. [https://doi.org/10.1016/j.energy.2005.10.023]
• Wang, J.-J., Y.-Y. Jing, C.-F. Zhang, and J.-H. Zhao, (2009), “Review on Multi-Criteria Decision Analysis Aid in Sustainable Energy Decision-Making”, Renewable and Sustainable Energy Review, 13, p2263-2278. [https://doi.org/10.1016/j.rser.2009.06.021]
• Kahraman, C., Î. Kaya, and S. Cebi, (2009), “A Comparative Analysis for Multiattribute Selection among Renewable Energy Alternatives Using Fuzzy Axiomatic Design and Fuzzy Analytic Hierarchy Process”, Energy, 34, p1603-1616. [https://doi.org/10.1016/j.energy.2009.07.008]
• Kaya, T., and C. Kahraman, (2011), “Multicriteria Decision Making in Energy Planning Using a Modified Fuzzy TOPSIS Methodology”, Expert Systems with Applications, 38, p6577-6585. [https://doi.org/10.1016/j.eswa.2010.11.081]
• Jahanshahloo, G. R., F. H. Lotfi, and M. Izadikhah, (2006), “An Algorithmic Method to Extend TOPSIS for Decision-making Problems with Interval Data”, Applied Mathematics and Computation, 175, p1375-1384. [https://doi.org/10.1016/j.amc.2005.08.048]
• Jahanshahloo, G. R., F. H. Lotfi, and A. R. Davoodi, (2008), “Extension of TOPSIS for Decision-making Problems with Interval Data”, Applied Mathematics and Computation, 181, p1544-1551.
• Chen, T.-Y., and C.-Y. Tsao, (2008), “The Interval -valued Fuzzy TOPSIS Method and Experimental Analysis”, Fuzzy Sets and Systems, 159, p1410-1428. [https://doi.org/10.1016/j.fss.2007.11.004]
• Baños, B., F. Manzano-Agugliaro, F. G. Montoya, C. Gil, A. Alcayde, J. Gómez, (2011), “Optimization Methods Applied to Renewable and Sustainable Energy: A Review”, Renewable and Sustainable Energy Reviews, 15, p1753-1766.
• Beccali, M., M. Cellura, and M. Mistretta, (2003), “Decisionmaking energy planning; Application of the ELECTRE method at regional level for the diffusion of renewable energy technology”, Renewable Energy, 28, p2063-2087.
• Wang, W.-P., (2009), “Evaluating New Product Development by Fuzzy Linguistic Computing”, Expert System with Application, 36, p9759-9766.
• Kahraman, C., and Î. Kaya, (2010), “A Fuzzy Multicriteria Methodology for Selection among Energy Alternatives”, Expert Systems with Applications, 37, p6270-6281. [https://doi.org/10.1016/j.eswa.2010.02.095]
• Klir, G. J., and B. Yuan, (1995), Fuzzy Sets and Fuzzy Logic: Theory and Applications, Prentice-Hall Inc.
• Kaufmann, A., and M. M. Gupta, (1991), Introduction to Fuzzy Arithmetic: Theory and Applications, New York, Van Nostrand Reinhold.
• Dubois, D., and Prade, (1980), Fuzzy Sets and Systems’ Theory and Applications, New York, Academic Press Inc.
• Chen, C.-T., (2000), “Extension of the TOPSIS for Group Decision-making Under Fuzzy Environment”, Fuzzy Sets and Systems, 114, p1-9. [https://doi.org/10.1016/s0165-0114(97)00377-1]
• Hwang, C.-L., and K. Yoon, (1981), Multiple Attribute Decision Making: Methods and Applications, Berlin, Springer-Verlag.
• Rouhani, S., M. Ghazanfari, and M. Jafari, (2012), “Evaluation Model of Business Intelligence for Enterprise Systems Using Fuzzy TOPSIS”, Expert Systems with Applications, 39, p3764-3771. [https://doi.org/10.1016/j.eswa.2011.09.074]
• Zhao, R., and R. Govind, (1991), “Algebraic Characteristicics of Extended Fuzzy Number”, Information Science, 54, p103-130.