개방형 지열 시스템 설계 방법의 개선 및 적용

1. 서 론

지구 온난화에 따른 기후변화 문제 및 화석 에너지 고갈은 신재생에너지의 사용 중요성을 증대시켜 왔다. 정부의 ‘저탄소 녹색성장’국가비전 제시 이후 신재생에너지 활용에 대한 필요성이 본격화되었다. 신재생에너지 중 지열에너지를 이용한 냉난방 시스템은 다른 에너지원을 사용한 냉난방 시스템보다 가장 효율적이고 친환경적인 에너지로써 해마다 생산량이 증가하고 있다. 지열 냉난방 시스템은 초기 투자비용이 다른 에너지원들보다 상대적으로 많이 소요된다는 단점이 있다. 하지만 기존 지열 시스템 연구 자료에 따르면 2009~2010년 설치된 지열 시스템이 기존 냉난방 시설과 비교하여 연간 85.8% 정도의 에너지 절감효과가 있어 5년 내에 초기 투자비용을 회수할 수 있을 것으로 예상하였으며, 이산화탄소 발생량이 약 35% 정도 감소한 것으로 분석되었다.^[1] 지열 냉난방 시스템은 지열을 추출하거나 건물 내에서 방출된 열을 지중으로 방출하기 위해 여러 가지 형태의 열교환기를 지중에 설치한다. 지중 열교환기는 지반과 직접 접촉하여 열에너지를 교환하는 매개체이기 때문에 지열 냉난방 시스템의 성능을 좌우하는 가장 중요한 요소이다. 지중 열교환 방식에 따른 종류는 크게 밀폐형(closed loop system)과 개방형(open loop system)으로 나뉜다. 밀폐형 시스템은 밀폐된 관로를 따라 순환수가 순환하는 형태로 열교환 매질과 간접적으로 접촉한다. 반면 개방형 시스템은 지하수 또는 지표수를 직접 수중모터펌프로 지상으로 끌어올려 에너지원으로 사용하는 방식으로 지하수 또는 지표수와 직접 열 교환을 하기 때문에 밀폐형보다 상대적으로 효율이 높다고 평가받고 있다.^[2,3]

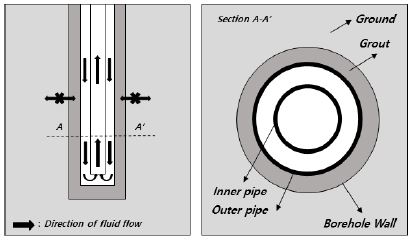
따라서 본 연구에서는 현행 국내 개방형 지열 냉난방 시스템 설계의 문제점을 도출하여 개선된 설계 방법을 제안하고, 이를 수치적으로 적용하여 개선 전･후를 비교･분석하고자 한다. 이를 위해 개방형 지열 냉난방 시스템의 가장 대표적인 지중 열교환기 형태인 우물 관정형 지중 열교환기(Fig. 1)를 대상으로 연구하였으며, 유한요소 상용 프로그램인 COMSOL Multiphysics로 우물 관정형 지중 열교환기에 대한 현장 열응답 결과를 해석하였다.

Fig. 1.

Open loop system (Standing Column Well)

2. 개방형 지열 시스템 설계 방법의 문제점

2.1 개방형 지열 시스템 설계 방법

개방형 지열 냉난방 시스템에 대한 대표적인 설계 방법은 신･재생에너지센터 공고 제2015-2호의 ‘신･재생에너지설비의 지원 등에 관한 지침’에 명시되어 있다. 이는 한국에너지공단의 각종 지원 사업에 포함되거나 신･재생에너지 설치의무기관에서 신･재생에너지설비 설치 시 준수해야할 사항이다. 이러한 사항에 해당되지 않는 경우 지침을 고려하지 않아도 되지만 국내 대다수의 개방형 지열 냉난방 시스템들이 이 지침에서 제시된 설계 방법을 사용하고 있다.

개방형 지열 냉난방 시스템의 설계 기준은 충분한 열용량을 확보할 수 있어야 하며, 설계 프로그램은 부하 특성, 지중 조건, 열전달 특성, 지열 열펌프 특성 등을 반영하고, 장기간 운전에 따른 지중 열 환경 변화를 예측할 수 있어야 한다고 명시되어 있다. 또한 개방형 지열 냉난방 시스템의 설계 프로그램은 GLHEPro를 이용하도록 지정하였으며, 이 외의 설계 방법 및 프로그램은 신재생 에너지 센터 자문위원회의 심의를 받아야 한다고 규정하고 있다. 실제로 현재 우물 관정형 지중 열교환기의 대부분은 GLHEPro를 이용하여 설계되고 있다. 시뮬레이션 기간을 20년 이상 설정하여 EWT 변화를 분석하고, 그 결과가 설계 시 적용한 냉방 시 EWT~난방 시 EWT 범위 내에 있어야 한다.

지중 열전도도 측정은 Table 1에 따라 실시하며, 시험공 길이는 설계하는 우물공보다 반드시 짧아야 한다. 초기 지중온도는 2시간 이상 가열 없이 펌프를 구동하여 순환수 온도 측정을 통해 이루어진다. 보일러 열량 투입 후 24시간 연속 측정하며, 측정 데이터는 10분 이하의 간격으로 수집하여 라인소스법(line source method)에 의해 지중 열전도도를 계산해야 한다.^[4] 단순화된 라인소스법은 식 (1)과 같다.

Table 1.

List of measurement guide for ground heat conductivity test

$\[ \lambda =\frac{Q/L}{4\mathit{\pi a}} \]$

(1)

여기서 λ는 지중 열전도도, Q는 순환수 전달 열량, L은 지중 열교환기 길이, a는 로그(log)시간에 대한 순환수 온도의 평균 기울기를 의미한다.

2.2 현행 설계 방법의 문제점

GLHEPro는 밀폐형 지중 열교환기를 설계하기 위한 프로그램으로써 3가지 형태(U-tube, double U-tube, concentric)만 설계가 가능하다.^[5] 그 중 동심이중관형(concentric)이 우물 관정형 지중 열교환기와 형태가 유사하다는 이유로 설계에 사용되고 있는 실정이다. 동심이중관형 지중 열교환기는 Fig. 2와 같이 보어홀(borehole) 내부에 2개의 크기가 다른 관을 동심원 형태로 겹쳐지게 설치하고 큰 관과 보어홀 벽면 사이의 공간은 그라우트(grout)로 채우는 수직 밀폐형 지중 열교환기의 한 가지 형태이다. 내･외부 파이프 사이의 환형 공간에 순환수가 흐르면서 외부 지반과 열을 교환하는 원리로 내부 파이프와 외부 파이프가 주입관 및 환수관의 역할을 하게 된다.

Fig. 2.

Concentric ground heat exchanger

동심이중관의 기본 형태를 고려했을 때 우물 관정형 지중 열교환기와 가장 큰 차이점은 외부 파이프(outer pipe)와 그라우트(grout)로 밀폐되어 순환수가 지하수와 섞이지 않는다는 점이다. 우물 관정형 지중 열교환기는 주변 지반의 지하수를 직접 순환시켜 상대적으로 높은 열전달 효과를 갖게 된다. 또한 개방형 시스템의 특성상 수리적 요소들(수리전도도, 저류계수, 지하수 흐름 등)에 의한 영향을 많이 받게 된다.^[6] 따라서 GLHEPro에서 설계를 위한 지반의 열전도도를 우물 관정형 현장 열응답 시험결과로 적용한다고 해도 실제 우물 관정형 열교환기의 강화된 열전달 효과를 제대로 반영하기 어렵다.

3. 설계 방법 개선

2장에서 GLHEPro를 이용한 우물 관정형 지중 열교환기 설계 방법에 대한 문제점을 알아보았다. 3장에서는 3가지 사례에 대한 현장 열응답 시험의 수치해석을 통해 용적열용량에 따른 강화된 열전도도의 변화와 설계 길이의 변화를 분석하였으며, 수치해석으로 산출된 보어홀 열저항을 적용하는 방법을 제시하였다. 또한 개선 전･후 설계 결과를 비교하여 개선 효과를 분석하였다.

3.1 수치해석 검증

3.1.1 현장 열응답 시험 조건

수치해석 검증을 위한 분석 사례는 세종정부청사 2구역, 마포구민 체육센터, 이순신 종합운동장으로 현장 열응답 시험 조건은 Table 2와 같다.^[7,8,9]

Table 2.

Conditions for example thermal response tests

초기 조건에서 총 수두를 ‘0’으로 가정하여 지하수 흐름이 없는 것으로 가정하였다. 깊이에 따른 지반 온도의 변화는 초기 지표온도와 지온경사를 이용하여 식 (2)와 같이 적용시켰다. 초기 지표온도와 지온경사는 한국에너지기술연구원의 신재생에너지 자원데이터센터에서 지역별 지온경사 측정 자료를 통해, 초기온도, 공저온도, 지온경사 측정 자료를 참고하여 적용하였다.^[10] 이 데이터는 실제 시추공에서 측정된 것이며, 우물 관정형 지중 열교환기의 심도는 통상 300~500m 이므로 외기온도 조건보다 지역별 지온경사에 의해 지중온도가 변화한다.

$\[ T=\left(\mathit{초기\; 지표온도}\left(℃\right)\right)-\left(\frac{\mathit{지온경사}\left(℃/m\right)}{\mathit{깊이}\left(m\right)}\right) \]$

(2)

3.1.2 수치해석 모델링

기본적으로 2차원 축대칭 모델을 적용하였으며, 지하수위 하부만을 모델링하였다. 적정 채수량 양수에 의해 수위강하가 발생하나, 그에 따른 열교환 길이 손실은 전체 열교환 길이에 비해 크지 않아 고려하지 않았다.^[11] 다공질 매질의 수리, 열적 지배방정식은 다음과 같다.^[12]

$\[ \begin{array}{c}\frac{\partial }{\partial t}\left(\rho {ϵ}_p\right)+\nabla \cdot \left(\mathit{\rho u}\right)=Q_m\\ \frac{\partial }{\partial t}\left(\rho {ϵ}_p\right)=\rho S\frac{\partial p}{\partial t}\end{array} \]$

(3)

$\[ \begin{array}{c}u=-\frac{K}{\mathit{\rho g}}\left(\nabla p+\rho g\nabla D\right)\\ {\left({\mathit{\rho C}}_p\right)}_{\mathit{eq}}\frac{\partial T}{\partial t}+\rho C_{p}u\cdot \nabla T=\nabla \cdot \left(k_{\mathit{eq}}\cdot \nabla T\right)+Q\end{array} \]$

(4)

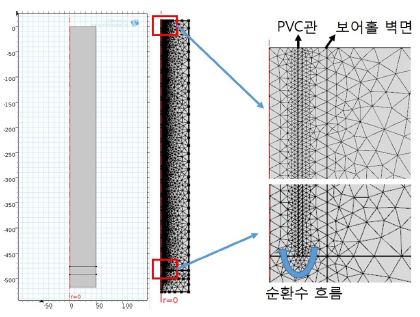
여기서 ρ는 밀도, ϵ_p는 공극률, u는 유속, Q_m은 질량 소스항, S는 저류계수, p는 압력, K는 수리 전도도, ∇D는 중력방향 길이차 벡터, (ρC_p)_eq는 다공질 매질의 등가 용적 열용량, k_eq는 다공질 매질의 등가 열전도도, Q는 열원을 의미한다. 해석 시간과 정확성을 고려하여, 격자는 총 약 100만개의 삼각요소를 가지는 2차원 축(axis)대칭 모델을 적용하였다. 최소 격자의 크기는 약 6mm이다. 열전달이 발생되는 부분인 축 부근에서는 최대한 격자를 작게 하였으며, 주위 지반으로 갈수록 격자를 성글게 구성하였다. 세종정부청사 2구역은 지반 크기를 폭 50m, 깊이 518m로 구성하였으며, 보어홀은 반경 100mm, 깊이 493m(= 보어홀 깊이 506m – 지하수 안정수위 5m – 무공관 길이 8m)로 모델링하였다. PVC 파이프는 두께 5cm, 길이 476.98m(= 493m – 유공관 길이 16m)로 모델링하였다. 파이프 길이를 2cm 줄인 이유는 파이프 요소망 형성 시 프로그램의 오류로 인한 문제를 최소화하기 위함이다. 최소 격자의 크기는 약 6mm이며, 파이프 두께는 약 7mm이다. 전체 파이프의 길이 477m로, 전체 열전달 영역을 고려하면 2cm에서의 열전달은 무시해도 될 정도로 매우 작을 것으로 판단하였다. 요소망 구성은 Fig. 3과 같다. 개방형 지열 시스템의 경우, 밀폐형 지열 시스템과 달리 지하수를 열전달 매질로 직접 이용한다. 순환수와 주변 지반의 열전도와 동시에, 주변 지반에서의 유입 및 유출과 공내의 순환수 흐름에 의해 발달되는 대류도 동시에 고려해야한다. 파이프의 두께가 7mm이지만, 길이는 490m이므로 모델의 경계조건에 의한 영향을 최소화하기 위해 지반을 폭 50m, 깊이 518m로 설정하였다. 이에 최소 격자는 파이프 두께에 적용되고, 이를 경계로 보어홀 벽면과 주변 지반의 격자를 생성하였다.

Fig. 3.

Numerical modeling of Sejong site

다른 사례들에서도 요소망은 삼각형으로 구성하였으며, 기본 형상은 세종정부청사 2구역과 동일하다. 순환수의 흐름은 유입 및 유출부에 평균유량을 기준으로 동일한 질량유량을 적용하였다(Fig. 4).

Fig. 4.

Circulating water of Sejong site

3.1.3 수치해석 조건

보어홀 내부의 흐름은 지반의 흐름과 다르게 다르시의 법칙(Darcy’s law)이 적용되지 않고 나비에-스토크 방정식(Navier-Stoke)을 따르지만, Neville and Tonkin(2004)에 의하면 아주 큰 투수계수 값을 사용하여 다르시(Darcy’s law)의 법칙이 적용 가능하다.^[13] 순환수의 흐름(거칠기를 가지는 보어홀 벽면, 매끈한 관내)을 모사하기 위해, 마찰계수는 Colebrook,^[14] Swanmee and Jian,^[15] Filonenko^[16]의 경험식을 이용하였으며, Nusselt 수의 경우에는 Gnielinski^[17]와 Bhatii and Sharh^[18]의 경험식을 이용하였다. 앞의 경험식은 천이, 난류흐름에 적용가능하나, 천이구간에서 신뢰성 있는 마찰계수식이 존재하지 않는다. 이에, 다른 상용 프로그램과 마찬가지로 선형 보간법을 이용하여 천이구간의 마찰계수를 산정하였다.

초기조건은 지표에는 대기압 조건과 비흐름(no flux) 조건을 설정하였으며, 지표면 온도를 설정하였다. 총 수두를 ‘0’으로 가정하였으며, 깊이에 대한 온도변화는 초기 지표온도와 지온경사를 이용하여 설정하였다. 열응답 시험(TRT)은 일정한 열량을 투입한 후, 순환수의 온도를 측정하여 지반으로 전달된 열량 및 지중 열물성을 산출한다. 식 (5)를 이용하여, 동일한 유량을 뉴먼(Neumann) 경계조건으로 하였다.

$\[ Q=C_p\cdot \stackrel{\text{̇}}{m}\cdot \left(T_{\mathit{enter}}-T_{\mathit{out}}\right) \]$

(5)

여기서 Q는 열원, 즉 순환수의 전달 열량, C_p는 순환수의 비열, $$ \stackrel{\text{̇}}{m}$$은 순환수의 질량유량, T_enter는 유입수의 온도, T_out은 유출수의 온도를 의미한다. 또한 초기 순환수의 유입 온도는 초기 지중온도와 동일하게 디리클레(Dirichlet) 경계조건으로 설정하였다. 식 (5)에서 비열과 유량이 고정되면, 온도의 차이(T_enter-T_out)를 이용하여 열량 투입 적용이 가능하다. 이러한 과정을 통해 경계조건을 유출 온도에 입･출구 평균온도차를 더하여 매 단계마다 설정되도록 하였다. 초기 지중온도 및 입･출구 평균온도차는 실제 지열 이용검토서에 제시된 현장 열응답 시험 결과를 적용하였다.

3.1.4 수치해석 결과

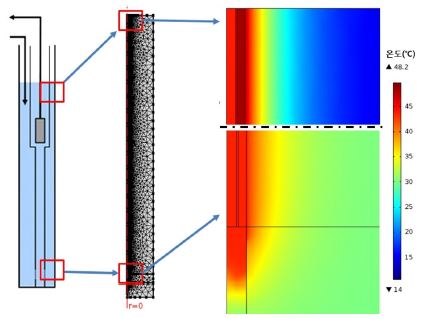
수치해석 결과 24시간 경과 시 이순신종합운동장의 우물 상단부 및 하단부의 온도 분포는 Fig. 5와 같다. 우측상단 그림에서 주위 지반의 온도는 초기 지표온도와 같이 약 15℃를 보이나, 순환수 온도(약 48℃)에 의해 열이 공내에서 지반으로 확산된다. 우측하단 그림에서 주변 지반온도가 지온경사에 의해 약 32℃ 정도로 형성되며, 순환수가 공내에서 순환하면서 온도가 낮아진 것을 볼 수 있다. 이와 유사하게 다른 사례들에서도 순환수 온도가 상승함에 따라 점차 지반으로 열이 확산되는 온도 분포가 나타났다.

Fig. 5.

Result of numerical analysis (Temperature distribution after 24 hours operation)

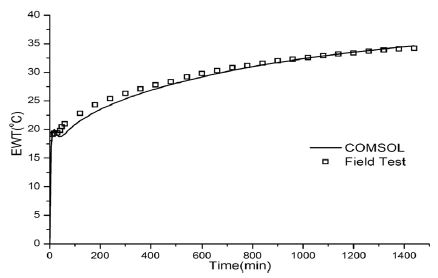
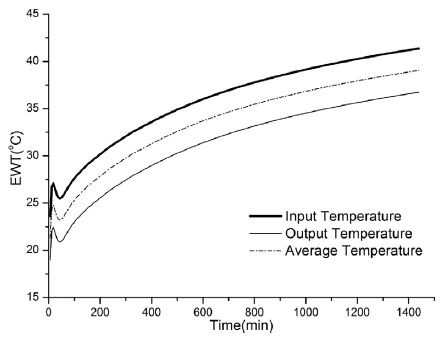
실제 현장 열응답 시험과 수치해석의 순환수 온도는 Fig. 6, 7, 8과 같다. 여기에서 순환수 온도는 순환수가 지중 열교환기에서 나오는 부분에서의 온도를 측정하였다. 수치해석 결과는 초기 0~60분 구간만 제외하고 실제 데이터와 거의 일치하였다. 모든 현장에서 초기 0~60분 구간의 수치해석 결과와 실제 데이터가 모두 일시적으로 상승하였다. 이는 현장 열응답 시험의 초기 순환수 온도가 주변 지반에 비해 가파르게 상승하여 발생하는 현상으로 판단된다. 수치해석에서 온도 상승폭이 상대적으로 큰 이유는 실제 현장 열응답 시험 전 초기 지중온도 측정을 위해 2시간 이상 가열 없이 펌프를 구동하게 되면서 보어홀 주변 온도가 심도와 관계없이 비슷해짐에 따라 온도경사가 상대적으로 작아지기 때문이라고 예상된다. 초기 1시간 경과 후 부터는 실제 데이터와 거의 유사하게 온도가 측정된다. 신･재생에너지설비의 지원 등에 관한 지침의 우물 관정형 지중 열교환기의 지중 열전도도 측정 항목 및 기준에서 초기 제외시간을 ‘시험 시작 후 2시간 데이터 제외’로 규정하고 있으므로 초기 2시간 경과 후 데이터 활용에는 문제가 없을 것으로 판단된다.

Fig. 6.

Variation of water temperature in Sejong

Fig. 7.

Variation of water temperature in Mapo

Fig. 8.

Variation of water temperature in Asan

3.2 보어홀 열저항 추정 및 적용

균등한 온도와 열 유속(heat flux)이 작용하는 보어홀에 대해 열저항이 유도되며, 이는 유체 흐름에 따라 변화하는 온도뿐만 아니라 유로들(flow channels)간의 열 교환 효과도 포함한다. 보어홀 열저항 방정식은 일반적으로 식 (6)과 같다.^[19]

$\[ R_b=\frac{T_f-T_b}{Q/L} \]$

(6)

여기서, T_f는 순환수 평균온도, T_b는 보어홀 벽면의 평균온도, Q는 순환수 투입 열량, L은 지중 열교환기 길이를 의미한다.

현장 열응답 실험의 수치해석을 통해 얻은 순환수 평균온도와 보어홀 벽면 평균온도를 적용하여 보어홀 열저항을 구하였다. 그리고 Table 3과 같이 기존 설계 방법인 GLHEPro로 산출한 보어홀 열저항과 설계 길이를 비교해보았다. 데이터를 분석한 결과, 수치해석으로 산출된 보어홀 열저항이 기존 설계 방법으로 구한 값보다 약 43% 정도 작게 나타나며, 설계 길이도 약 5% 정도 감소하는 것을 알 수 있었다. GLHEPro에서는 밀폐형인 동심이중관형으로 산출하기 때문에 수치해석 보다 상대적으로 큰 보어홀 열저항이 산출되는 것으로 판단된다. 그러므로 수치해석을 통해 보어홀 열저항을 산출하여 설계에 적용하는 것이 더욱 정확할 것이며, 보다 경제적인 설계가 가능하다.

Table 3.

Comparison of borehole thermal resistance and length

4. 군 시설 적용 예시

4.1 ○○사관학교 병영시설

○○사관학교 내 병영시설 중 한 곳을 선정하여 개선된 개방형 지열 시스템 설계를 적용해보았다. 적용 대상 병영시설의 건물 개요는 Table 4와 같으며, 실제 월별 건물 부하량(Table 5)을 기준으로 설계하였다.^[20] 현장 열응답 시험은 수치해석으로 대체하여 실시하였다.

Table 4.

Outline of the OO military academy barracks

Table 5.

Monthly load of the OO military academy barracks

가상의 지중 열교환기 크기는 마포구민 체육센터와 동일하게 적용하였으며, 지반 초기온도는 실제 온도를 사용하였다. 기타 지반 조건은 우리나라 화성암의 열물성 평균값을 적용하였다.^[21] 수치해석으로 현장 열응답 시험을 모사하고(Fig. 9) 라인소스법을 이용해 지중 열전도도를 구한 결과 3.1816W/m･K로 산출되었다.

Fig. 9.

Variation of water temperature in thermal response test

4.2 개선 전･후 설계 비교

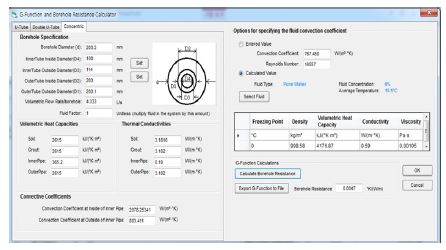
GLHEPro를 이용한 현행 설계 방법으로는 보어홀 열저항이 0.0047m･K/W로 산출되었다(Fig. 10). 또한 지중 열교환기 길이는 7,273m로 설계되었다.

Fig. 10.

Calculation of borehole thermal resistance by using GLHEPro

개선된 설계 방법으로 보어홀 열저항을 산출하기 위해 현장 열응답 시험의 수치해석 결과를 사용하였다. 순환수 평균온도와 보어홀 벽면의 평균온도를 적용하여 보어홀 열저항이 0.002737m･K/W로 산출되었다. 이에 따라 지중 열교환기의 설계 길이는 7,120m으로 개선 전 설계 길이보다 153m 정도 감소하였다(Table 6).

Table 6.

Improvement by new design method (Resistance and length of borehole)

개선된 설계 방법 적용 시 동심이중관형이 아닌 개방형으로 보어홀 열저항을 산출하기 때문에 상대적으로 보어홀 열저항이 감소하게 되며, 이로 인해 설계 길이가 감소하여 시공 비용을 절감할 수 있을 것이다.

5. 결 론

지열 냉난방 시스템 중 개방형 시스템은 지하수 또는 지표수와 직접 열 교환을 하기 때문에 밀폐형보다 상대적으로 효율이 높다고 평가받고 있다. 향후 개방형 지열 냉난방 시스템의 도입이 증가할 것으로 예상되나 아직 개방형 지중 열교환기에 대한 설계 방법의 표준화가 미흡한 실정이다. 따라서 본 연구에서는 현행 국내 개방형 지열 냉난방 시스템 설계의 문제점을 도출하여 개선된 설계 방법을 제안하고, 이를 군 시설(○○사관학교 병영시설)에 적용하여 개선 전･후를 비교･분석하였다.

연구 진행을 위해 유한요소 상용 프로그램인 COMSOL Multiphysics로 우물 관정형 지중 열교환기에 대한 현장 열응답 시험을 해석하였다. 개방형 지열 시스템 설계 변수 중 하나인 보어홀 열저항을 수치해석으로 추정하여 적용하는 방법을 제안하였으며, 이를 3가지 실제 현장 사례에 적용하여 비교하였다. 수치해석으로 산출된 보어홀 열저항이 기존 설계 방법으로 구한 값보다 약 43% 정도 작게 나타났으며, 설계 길이도 약 5% 정도 감소하는 개선 효과를 확인하였다.

개선된 설계 방법을 군 시설물인 ○○사관학교 병영시설에 적용한 결과 보어홀 열저항이 42%, 설계 길이는 2% 감소하였다. 따라서 개선된 개방형 지열 시스템 설계 방법을 적용하면 지중 열교환기 길이의 과도한 설계를 방지하는 효과가 있다고 판단된다.

본 연구에서 수행된 수치해석은 일부 지반 조건들을 생략 또는 가정하였기 때문에 향후에는 더 정확한 해석이 가능하도록 보완해야할 것이다. 특히 지하수 흐름의 영향을 확인하기 위해서는 3차원 모델을 사용해야 할 것이다. 본 연구를 통해 설계 개선안을 제시하였지만 GLHEPro의 동심이중관형 설계 방법을 이용한 것이므로 개선된 설계 방법의 오차가 발생할 것이다. 또한 수치해석을 수행해야하는 소요가 추가로 발생하고, 수치해석 결과가 현장 데이터와 큰 차이가 있을 경우 보어홀 열저항 추정 값 활용이 불가한 단점들도 있다. 비록 이번 연구에서는 설계 변수들 중에서 보어홀 열저항만을 개선하였지만 향후에는 개방형 지열 시스템 고유의 설계 방법을 개발한다면 정확한 설계가 가능할 것이다.

Acknowledgments

본 연구는 2015년 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(2013R1A2A2A010 67898)과 국토교통부 국토교통기술지역특성화의 연구비지원(16RDRP-B076564-03) 일환으로 수행되었습니다.

References

• Kim, S. W., (2012), “A Case Study on the Geothermal-System Analysis of Military Facilities”, Master Thesis, Honam University.
• Kwon, K. S., Lee, J. Y., and Mok, J. K., (2012), “Update of current status on ground source heat pumps in Korea (2008-2011)”, The Geological Society of Korea, 48(2), p193-199.
• Na, S. M., Park, S. S., Park, J. H., Rhee, K. J., and Kim, T. W., (2009), “A Case Study on the Installation and Operation of the Standing Column Well Method”, Annual Spring Meeting of The Korean Society for New Renewable Energy, 9, p592-595.
• Carslaw, H. S., and Jaeger, J. C., (1959), “Conduction of heat in solids”, 2nd ed., Oxford, Clarendon Press.
• IGSHPA, (2014), “GLHEPro 4.1 Users’ Guide”, School of Mechanical and Aerospace Engineering Oklahoma State University.
• Bae, S. M., Nam, Y. J., and Hwang, S. H., (2016), “Sensitivity Analysis of Design Factor for the Suitable Map of Ground Source Heat Pump System”, Journal of the Korean Society for New and Renewable Energy, 12(2), p65-70. [https://doi.org/10.7849/ksnre.2016.10.12.S2.65]
• National Agency for Administrate City Construction, (2009), “Geothermal energy assessment report (Government office building Stage 1 Section 2)”.
• Mapo-gu district office, (2015), “Geothermal energy assessment report (Mapo gumin sports center)”.
• Asan City Hall, (2015), “Geothermal energy assessment report (Admiral Yi Sun-shin stadium and complex sports center)”.
• New & Renewable Energy Data Center, Korea Institute of Energy Research, http://kredc.kier.re.kr.
• Deng, Z., (2004), “Modeling of Standing Column Wells in Ground Source Heat Pump Systems”, Doctor Thesis, Oklahoma State University.
• Comsol Inc, (2015), “Comsol Multiphysics Reference Manual Version. COMSOL 5.1.”, USA.
• Neville, C. J., Tonkin, M. J., (2004), “Modeling multiaquifer wells with MODFLOW”, Ground Water, 42(6), p910-919. [https://doi.org/10.1111/j.1745-6584.2004.t01-9-.x]
• Colebrook, C. F., (1939), “Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipes laws”, J Inst Civ Eng, 11, p133-156. [https://doi.org/10.1680/ijoti.1939.13150]
• Swanmee, P. K., Jian, A. K., (1976), “Explicit equations for pipe-flow problems”, J Hydraulic Div ASCE, 102, p674-677.
• Filonenko, G. K., (1954), “Hydraulic resistance in pipes (in Russian)”, Teploenergetiki, 1(4), p40-44.
• Gnielinski, V., (1976), “New equations for heat and mass transfer in turbulent pipe and channel flow”, Int Chem Eng, 16, p359-368.
• Kakac, S., Shah, R. K., Aung, W., (1987), “Handbook of sigle-phase convective heat transfer”, New York, John Wiley&Sons, Inc.
• Hellström, G., (1991), “Ground heat storage: Thermal analyses of duct storage systems”, University of Lund.
• Turbo Energy, (2009), “Geothermal energy assessment report (○○ Military Academy Barracks)”.
• Park, J. M., Kim, H. C., Lee, Y. M., Shim, B. O., and Song, M. Y., (2009), “Thermal properties of rocks in the Republic of Korea”, Economic and Environmental Geology, 42(6), p591-598.