풍력터빈 효율 향상을 위한 풍속전단 완화 펜스의 다구찌 강건설계
Copyright © 2016 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper proposes an optimal design method, which consists of computational fluid dynamics and Taguchi robust design method, for a wind shear mitigation fence installed at the upstream of a wind turbine to reduce the fatigue load on the blades and to augment the power generation. The fence generates a virtual hill effect, which mitigates wind shear by speedup of the lower part of the atmospheric boundary layer. For the design factors, the fence height, fence inclination angle, separation distance between the fence and wind turbine, wind speed, and turbulence intensity of the upstream wind profile are considered by constructing a L9 Taguchi orthogonal array. For the performance measures, the wind speed-up within a rotor plane of wind turbine and non-uniformity of the wind speed profile were evaluated. The main design factors were the fence height in terms of power generation augmentation and the separation distance in terms of the fatigue load mitigation. In the case of a 5 m fence installation, a 2% increase in wind speed and 42% decrease in non-uniformity was anticipated so that the substitution of a solid fence with a more practical windbreak is likely to be considered.
Keywords:
Wind shear mitigation fence, Taguchi robust design, Computational Fluid Dynamics(CFD), Wind turbine키워드:
풍속전단 완화 펜스, 다구찌 강건설계, 전산유체역학, 풍력터빈1. 서 론
풍력터빈의 설비용량은 1995년 1MW를 초과한 이후 계속적으로 증가하고 있으며, 이에 따라 풍력터빈의 크기 즉, 타워의 높이와 블레이드의 길이도 커지는 추세이다.
2014년말 기준으로 보급용 MW급 풍력터빈의 블레이드 평균길이(D/2)는 40m, 허브의 평균높이(h)는 80m로, 블레이드가 회전하는 구간은 지상 80m를 중심으로 최저높이 지상 40m에서 최고높이 지상 120m에 이르게 된다. 이러한 크기의 풍력터빈은 대기경계층 높이의 약 1/3에 해당하는 하단부에서 작동하게 된다.
대기경계층 하단부는 지면과의 마찰력에 의해 높이에 따른 풍속의 차이, 즉 풍속전단(wind shear)이 발생하는 영역이다. 블레이드에 작용하는 풍속전단은 풍력터빈에 주기적인 굽힘 모멘트(bending moment)를 부과하므로, 결국 블레이드와 축 베어링(shaft bearing)에 피로하중으로 작용하여 내구성에 손상을 준다.
최근에는 풍력터빈 나셀에 장착하는 라이다(LiDAR)로 풍력터빈에 입사되는 풍상부 풍속분포(upstream wind speed profile)를 측정하여 풍속의 변동과 풍속전단을 미리 파악하고 능동적으로 블레이드 피치를 제어(blade pitch control) 함으로써 추력에 의한 피로하중(fatigue load)를 완화시키는 기술이 개발되었다.[1,2]
다른 한편에서는 풍력터빈의 풍상부에 펜스와 같은 단순한 구조물을 설치하여 풍속분포를 변형시킴으로써 풍속전단을 완화시키는 방법도 제시되었다.[3] 또는 방조제와 같은 구조물 풍하측에 풍력터빈이 위치할 경우, 구조물에 의한 풍속증가가 발생함을 확인한 바도 있다.[4]
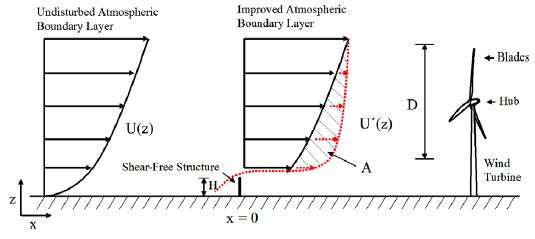
풍속전단 완화 펜스(wind shear mitigation fence; 이후 펜스)로 명명된 이 방법은 Fig. 1과 같이 풍력터빈의 풍상부 지면에 펜스 형태의 단순 구조물에 설치한다. 그리고 구조물에 의해 유도된 유동박리(flow separation)로 말미암아 펜스 직후방의 재순환 영역(recirculation zone)은 마치 가상의 언덕(virtual hill)을 형성하게 된다. 이 위를 지나는 바람은 가상 지형효과에 의해 U(z)로부터 U’(z)와 같이 변형된다. 즉, 대기경계층의 최하층부에 인위적인 변형을 유도하여 풍속을 증속(speedup) 시킴으로써 풍속전단을 완화시켜 결국 풍속의 연직분포를 수직으로 평평하게 만드는 것이다.
Schematics of a wind shear mitigation fence
Fig. 1에 표시된 영역 A는 가상의 언덕이 밀어내는 바람의 모멘텀에 의해 풍속분포의 하층부가 증속되는 모습을 보여주는데, 이러한 풍속분포의 변형은 궁극적으로 영역 A 만큼 평균풍속을 증가시키게 된다. 또한 평균풍속의 증가는 풍력터빈의 설비이용률(capacity factor)을 증가시키는 긍정적인 효과로 이어진다.
그러나 펜스를 현장에 적용하기 위해서는 먼저 다양한 바람조건(평균풍속, 풍속전단, 난류강도 등) 하에서 최고의 효과를 낼 수 있는 구조물의 치수(높이, 폭, 각도 등)와 설치위치 등을 결정할 수 있는 설계법이 필요하다.
본 연구에서는 다양한 바람조건 하에서 최대의 풍속전단 완화 효과를 낼 수 있는 펜스의 최적 설계법을 도출하기 위하여 다구찌 강건설계(Taguchi robust design)와 전산유체역학(CFD; Computational Fluid Dynamics)을 이용하였다. 즉, 다양한 바람조건과 펜스의 높이, 경사도, 설치위치 등에 따른 풍속전단의 완화 효과를 정량적으로 판단하기 위해 RANS(Reynolds Averaged Navier-Stokes) 수치해석을 수행하였고, 최적 설계범위를 결정하는 대표적인 직교설계 실험계획법(DOE; Design Of Experiments)인 다구찌 강건설계 방법을 이용하여 최소요인의 해석으로 최적 설계값을 도출하였다.
2. 연구방법
2.1 전산유체역학(CFD)
풍상부 펜스에 의해 변형되는 대기경계층 풍속분포의 특성을 정량적으로 파악하기 위하여 전산유체역학 해석프로그램인 SC/Tetra v9을 이용하였다. 단, 펜스의 폭이 충분히 넓다고 가정하여 2차원 수치해석을 수행하였다.
유동박리가 수반된 대기유동장의 수치해석 시 예측 정확도가 우수한 것으로 검증된 MP k-ε 난류모델(turbulence model)을 사용하였다.[5]
계산영역은 펜스의 전방으로 500m, 후방으로 1,500m 그리고 연직방향으로 500m의 크기로 설정하였다. 입구 경계조건(upstream boundary condition)은 지수법칙으로 표현되는 대기경계층 풍속분포와 난류분포를 설정하였으며 대기경계층의 높이(δ)는 300m로 설정하였다. 이를 수식으로 표현하면,
| (1) |
상부 경계조건(upper boundary condition)은 자연 유출조건(natural in-out flow)을 적용하였으며 지면 경계조건(ground boundary condition)으로는 초원 평지를 가정하여 지면거칠기 0.03m에 해당하는 풍속분포지수(α)인 0.2를 부과하였다. 대기경계층 높이 이상에서는 10m/s로 일정한 풍속의 지균풍(Ug)이 유지되는 것으로 가정하였다.
2.2 다구찌 강건설계
다구찌 강건설계는 상이한 인자들이 공정 성능특성(performance characteristics of process)의 평균 또는 분산(variance)에 얼마나 영향을 미치는지를 파악해내는 실험계획법이다. 다구찌는 공정에 영향을 미치는 비제어인자인 잡음인자(noise factor)를 배제할 수 있는 직교배열(orthogonal array)을 도입함으로써, 모든 가능한 요인들의 조합에 대해 실험을 수행하는 대신 주요인을 파악할 수 있는 최소한의 실험조합을 도출하여 해석에 소요되는 시간과 자원을 아낄 수 있도록 한다.[6]
일반적으로 다구찌 강건설계의 순서는 다음과 같다.[7]
(1) 공정의 목적(process objective)을 설정한다. 즉, 공정의 성능지표(performance measure)가 되는 목표값을 정한다. 공정의 목적은 목표값의 최대화 또는 최소화로 정의될 수 있으며, 성능이 목표값으로부터 멀어지는 정도를 손실함수(loss function)로 정의할 수 있다.
본 연구에서는 풍속전단의 감소율을 성능지표로 설정하고 그 최대화를 목적으로 설정하였다.
(2) 공정에 영향을 미치는 설계인자를 결정한다. 설계인자(design factor)라 함은 공정 내에서 성능지표에 영향을 미치며 제어가 가능한 변수를 의미한다. 변수의 조합으로 구성되는 실험조건의 최대 사례수를 고려하여 이들 변수의 분산 범위를 몇 단계로 할 것인지 결정한다.
본 연구에서는 사전 전산유체역학 수치해석을 수행하여 공정의 성능지표인 풍속전단 경감률에 영향을 주는 변수를 설계인자로 선정하였다.
(3) 실험설계를 위해 각각의 실험조건과 회수를 지정하는 직교배열(orthogonal arrays)을 구성한다. 직교배열의 구성은 인자의 수와 그 분산 수준에 따라 결정된다.
(4) 구성된 직교배열에 따라 실험을 수행한 후 각각의 인자들이 성능지표에 미치는 영향에 대하여 분석함으로써 목적을 달성할 수 있는 최적의 설계값을 결정한다.
2.3 성능지표
다구찌 설계를 위해서는 설계인자를 선정하고 설계목표의 달성 정도, 즉 성능지표를 평가할 수 있는 정량척도를 설정하여야 한다.
성능지표를 평가할 수 있는 정량척도로서 풍력터빈의 출력 증가에 기여하는 풍속증가(wind speedup; ΔS), 그리고 풍력터빈 블레이드의 피로하중에 영향을 미치는 풍속분포의 비균질도(non-uniformity of wind speed profile; ΔN)를 설정하였으며, 이에 대한 수학적 정의는 각각 Eqs. (2)와 (3)에 나타낸 바와 같다.
| (2) |
| (3) |
풍속증가는 풍상부 원방으로부터의 자연풍 U(z)에 대한 풍력터빈 위치에서의 변형된 풍속분포 U’(z)의 증가율을 나타내며 판단변수 중 망대특성(larger-the-better characteristics)으로 설정하였다. 즉, 평균풍속 증가가 커질수록 풍력터빈의 출력 증가를 기대할 수 있다.
풍속분포의 비균질도는 블레이드 회전구간의 최하단, 허브, 블레이드 최상단 높이인 40m, 80m, 120m에서의 풍속의 편차와 평균의 비율을 나타내며 풍력터빈의 블레이드 회전영역 전체에서의 풍속의 편차(deviation)를 나타내는 지표이다. 본 연구에서는 판단변수 중 망소특성(smaller-the-better characteristics)으로 사용하였다. 즉, 풍력터빈 블레이드 회전영역의 최상단과 최하단의 풍속 편차가 작을수록 풍속전단에 의한 굽힘 하중의 상쇄를 기대할 수 있다.
2.4 설계인자
성능지표에 영향을 미치는 설계인자를 선정하기 위하여 사전 전산유체역학 수치해석을 수행하여 펜스 주위를 지나는 대기유동장의 특성을 파악하였다. 수치해석 결과, 펜스에 의해 형성되는 가상 언덕의 높이와 길이가 풍하측 풍력터빈에 입사되는 풍속분포의 변형에 지배적인 영향을 미침을 확인할 수 있었다. 따라서 설계인자로는 펜스의 높이(H), 펜스의 경사각(θ), 펜스와 풍력터빈의 이격거리(L), 풍력터빈에 입사되는 풍속(U) 그리고 난류강도(TI; Turbulence Intensity)를 선정하였다.
설계인자의 수준 즉, 분산범위를 결정하기 위하여 기본모델(base model)을 설정하고, 나머지 설계인자를 모두 고정시킨 후 하나의 인자만을 변화시켜가며 수치해석을 수행하였다. 해석결과는 풍하측 거리에 대하여 판단변수(풍속증가, 비균질도)의 경향성을 분석한다. 경향성 비교 결과를 바탕으로 판단변수에 주된 영향이 끼치는 설계인자를 선별하고 다구찌 강건설계를 수행하여 각각의 설계인자의 영향도를 파악함으로써 최종적으로 설계영역을 도출할 수 있다. Table 1은 각각의 설계인자 및 수준을 나타낸다.
Level of design factors for tendency analysis
3. 연구결과 및 고찰
3.1 설계인자의 경향성 분석
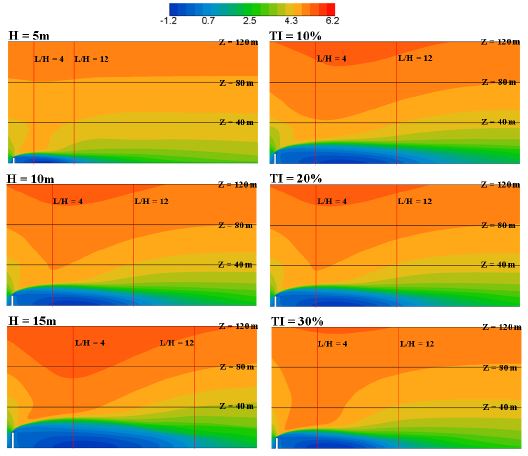
Fig. 2는 펜스를 지나는 대기유동장의 풍속 분포도를 도시한 그림으로, 좌측열은 펜스의 높이를 변화시켰을 때이고 우측열은 입사풍의 난류강도를 변화시켰을 때의 수치해석 결과이다.
Wind speed contour plots by fence height (left column) and turbulence intensity (right column)
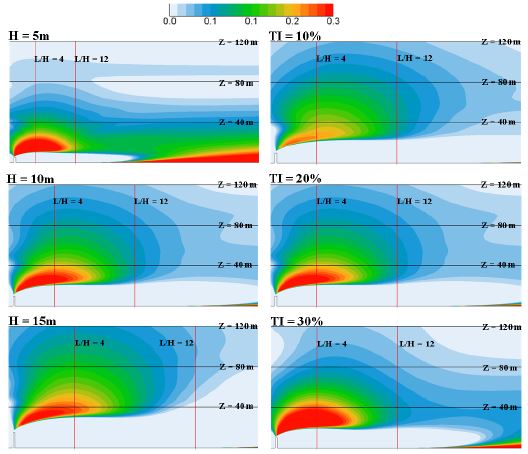
Fig. 3은 Eq. (2)로 정의된 풍속증가의 분포도를 도시한 그림으로, 역시 좌측열은 펜스의 높이를 변화시켰을 때이고 우측열은 입사풍의 난류강도를 변화시켰을 때의 수치해석 결과이다.
Wind speedup contour plots by fence height (left column) and turbulence intensity (right column)
Figs. 2와 3의 등고선 그림으로부터 펜스의 높이가 높아질수록 펜스 후방에 생성되는 재순환 영역의 크기가 커짐에 따라 대기경계층 하단부에서의 풍속증가도 커질 뿐 아니라 그 영역도 풍하측 및 상부로 크게 확장됨을 알 수 있다. 난류강도가 증가할수록 펜스 직후방에서의 풍속증가는 강화되지만 재순환 영역의 길이는 줄어드는 경향이 나타나는데, 이는 난류강도가 높으면 유동박리 지점에서 생성되는 레이놀즈 전단응력(Reynolds shear stress)을 증가시켜 유동의 혼합을 촉진시킬뿐 아니라 난류에너지 소산률도 커지기 때문에 결국 수평방향 모멘텀이 빨리 소진되어 박리유동의 재부착이 빨라지는 것으로 설명할 수 있다.[8]
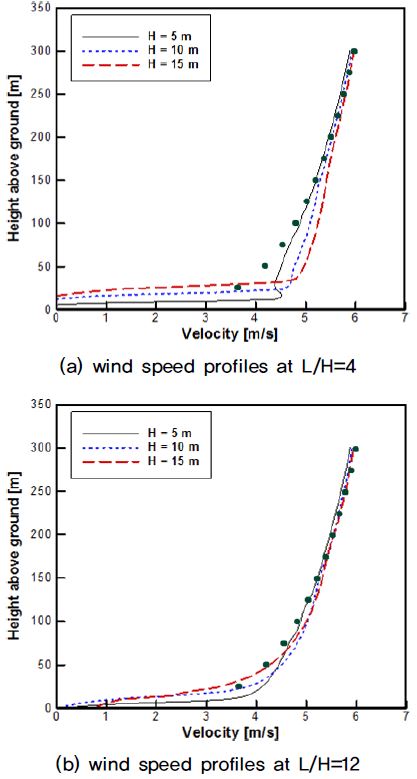
Fig. 4는 펜스의 높이에 따른 풍속분포의 변화를 비교한 그래프이다. 펜스 높이의 4배 풍하측인 L/H=4에서의 풍속분포는 펜스의 높이가 증가함에 따라서 특히 하단부의 풍속증가가 두르러짐을 보인다. 이러한 풍속증가는 풍속구배를 경감함으로써 풍속분포의 비균질도 역시 줄이는 효과가 있다. 그러나 풍하측으로 진행할수록 유동박리에 의한 가상의 언덕의 영향권에서 멀어지며 풍속분포가 자연풍으로 회복됨에 따라 풍속증가 효과도 점차 소멸되어 감을 확인할 수 있다.
Wind speed profiles behind a fence (black circles: wind profile without a fence)
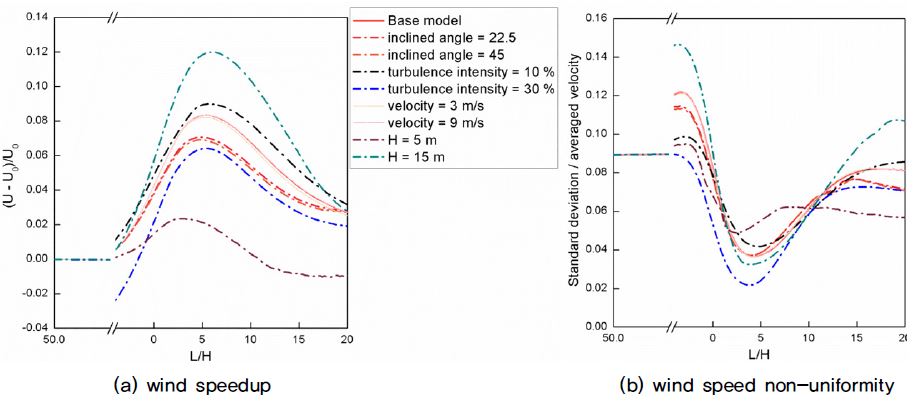
Fig. 5는 펜스와 풍력터빈의 무차원 이격거리(L/H)에 따른 판단변수의 경향성을 나타낸 그래프이다. 출력증가에 기여하는 풍속증가(ΔS)의 경우, 다른 인자들에 비해 펜스의 높이(H), 펜스의 경사각(θ), 입사풍 난류강도(TI)의 영향이 가장 두드러짐을 확인 할 수 있다. 반면 풍력터빈의 굽힘 모멘트에 기여하는 풍속분포 비균질도(ΔN)의 경우, 펜스의 높이(H) 및 입사풍 난류강도(TI)의 영향이 지배적으로 작용함을 확인할 수 있다.
그런데 펜스와 풍력터빈의 무차원 이격거리에 따른 모든 인자들의 변화양상은 증가하였다가 감소하는 동일한 경향을 보일뿐 아니라 최대/최소 극점(point of pole)의 위치도 유사함을 확인 할 수 있다. 이러한 경향성은 L/H가 다른 인자들에 대해서 독립적인 변수라는 것을 의미하는 것으로, 특히 3<L/H<10의 영역에서 성능지표의 최대값이 발생함을 알 수 있다. 따라서 다구찌 강건설계에서 설계인자의 수준을 결정할 때 관심구간을 3<L/H<10로 설정함이 바람직하다.
Horizontal distribution of performance measures along L/H and z=80m (hub height)
펜스 경사각(θ)의 경우, 판단변수에 영향을 미치기는 하지만 경사각이 없는 경우에 망대, 망소 특성 모두가 효율적인 결과를 보였으므로, 본 해석에서는 펜스의 경사각을 설계인자에서 배재하였다.
난류강도(TI)의 경우, 앞서 설명한 이유로 인하여 그 값이 작아질수록 풍속증가 효과가 큰 것을 확인 할 수 있다. 동일한 이유로 풍속분포의 비균질도는 입사풍의 난류강도가 30%일 경우 가장 우수한 결과를 보였다.
풍상부 원방에서 유입되는 대기경계층의 풍속의 변화에 따라서는 판단변수에 거의 영향을 끼치지 않는 다는 것을 알 수 있다.
3.2 최적설계의 도출
설계인자의 경향성 분석을 바탕으로 판단변수에 유의한 영향을 주는 인자로 펜스의 높이(H), 펜스와 풍력터빈의 무차원 이격거리(L/H) 그리고 난류강도(TI)를 선정하였다. 이들 3 인자에 대해 3 수준의 다구찌 해석(L9)을 수행하였으며 직교배열에 따른 성능지표 분석결과를 Table 2에 제시하였다.
Taguchi orthogonal array and analysis results
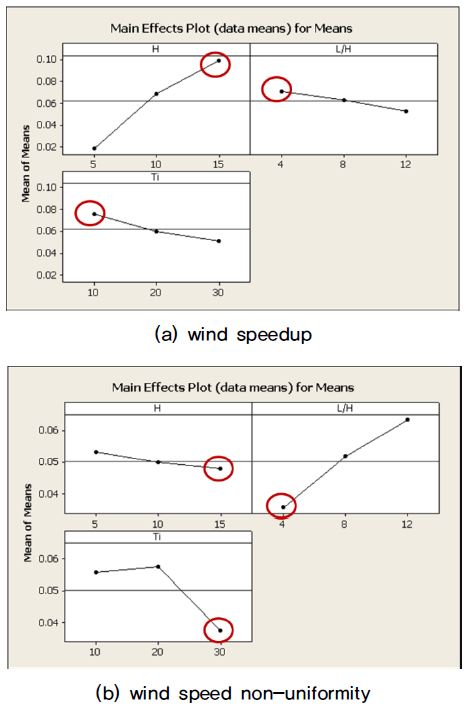
다구찌 해석 결과를 정리한 Fig. 6을 보면, 다인자 설계임에도 불구하고 앞서 설계인자의 경향성 분석과 동일한 특성이 나타났다. 즉, Table 3에 정리한 설계인자의 중요도에 따른 영향도를 보면, 풍속증가 측면에서는 펜스의 높이(H)가 가장 큰 영향을 미치며 풍속분포의 비균질도 측면에서는 무차원 이격거리(L/H)가 가장 큰 영향도를 보인다는 것을 알 수 있다.
Taguchi robust analysis results
Taguchi analysis results and performance rank
4. 결 론
본 연구에서는 풍력터빈의 피로하중 경감 및 발전량 증가를 위해 풍상부에 설치하는 풍속전단 완화 펜스의 최적 설계법을 도출하기 위하여 전산유체역학 수치해석법과 다구찌 강건설계법을 이용하였으며 다음과 같은 결론을 도출하였다.
- 1) 풍력터빈의 발전량 증가 관점(풍속증가)에서 가장 큰 영향을 미치는 설계인자는 펜스의 높이이며, 풍력터빈의 피로하중 경감 관점(풍속분포의 비균질도)에서 가장 큰 영향을 미치는 설계인자는 펜스와 풍력터빈간의 거리임 확인하였다.
- 2) 펜스의 높이가 5m일 때, 풍력터빈 블레이드 회전구간에서의 평균풍속 증가율은 2%, 펜스의 높이가 15m일 때는 10%의 성능향상 효과를 보였다. 반면 풍속분포 비균질도는 각각 42%와 78%가 감소하였다. 또한 펜스의 최적 설치위치는 3<L/H<10 구간임을 확인하였다.
- 3) 풍속전단 완화 펜스가 풍력터빈의 효율 향상에 유의한 수준의 효과가 있음을 확인하였으나, 본 연구에서는 수치해석의 수월성을 위해 2차원을 가정하였기 때문에 3차원 효과가 포함될 경우에는 그 효과가 다소 감소할 것으로 예상된다.
- 4) 다구찌 강건설계 결과, 펜스의 높이가 높을수록 긍정적인 개선효과가 기대되지만 설치비용을 고려할 때 부가적인 효용성이 있는 방풍림을 조성하는 방안을 검토할 수 있다. 단, 방풍림은 다공성을 가지므로 설계인자에 다공도(porosity)를 포함시켜 재검토하여야 할 것이다.[9]
Acknowledgments
본 연구는 한국에너지기술연구원의 주요사업으로 수행한 연구결과입니다(B6-2427).
References
-
Schlipf, D., Schlipf, D.J., Kuhn, M., (2013), “Nonlinear Model Predictive Control of Wind Turbines Using LIDAR”, Wind Energy, 16(7), p1107-1129.
[https://doi.org/10.1002/we.1533]
- Kim, H.G., and Woo, S.W., (2012), “A Wind Shear Mitigation Method to Improve Wind Turbine Performance”, J. of the Wind Engineering Institute of Korea, 16(4), p173-177.
- Kim, H.G., (2010), A Structure for Compensating Wind Velocity, Korea Patent 10-0969595.
-
Woo, S.W., and Kim, H.G., (2013), “Computational Flow Analysis on Wind Profile Change Projected to a Wind Turbine Behind Saemangeum Seawall”, New & Renewable Energy, 9(1), p6-11.
[https://doi.org/10.7849/ksnre.2013.9.1.006]
-
Rhee, H.N., Kim, T.S., Jeon, W.H., Kim, H.G., (2013), “Three-Dimensional Computational Flow Analysis on Meteorological-Tower Shading Effect”, J. of the Korean Solar Energy Society, 33(1), p1-6.
[https://doi.org/10.7836/kses.2013.33.1.001]
-
Yum, B.J., Kim, S.J., Seo, S.K., Byun, J.H., Lee, S.H., (2013), “The Taguchi Robust Design Method: Current Status and Future Directions”, J. of the Korean Institute of Industrial Engineers, 39(5), p325-341.
[https://doi.org/10.7232/JKIIE.2013.39.5.325]
-
Vuchkov, I.N., and Boyadjieva, L.N., (2001), Quality Improvement with Design of Experiments: A Response Surface Approach, Kluwer Academic Publishers, Dordrecht.
[https://doi.org/10.1007/978-94-009-0009-7]
-
Hattori, H., and Nagano, Y., (2010), “Investigation of Turbulent Boundary Layer Over Forward-Facing Step via Direct Numerical Simulation”, Int’l J. of Heat and Fluid Flow, 31, p284-294.
[https://doi.org/10.1016/j.ijheatfluidflow.2010.02.027]
- Kim, H.G., Lim, H.C., Lee, J.M., (1996), “Numerical Simulation of the Wind Flow Over a Triangular Prism with a Porous Windbreak”, J. of Korean Society for Atmospheric Environment, 15(3), p223-233.