Online publication date 18 Jun 2024
시뮬레이션 시간 단계에 따른 FOWT 서지방향 항력계수 결정에 관한 CFD해석 연구
Copyright © 2024 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, the effect of the time step specified in a computational fluid dynamics (CFD) simulation on load response is analyzed and the drag coefficients of the floating body of floating offshore wind turbines (FOWTs) are estimated. By evaluating the error in the FOWT load response and the change in the drag-coefficient values based on the density of the time intervals, this study aims to establish a time-interval setting that minimizes the time and cost of CFD simulations for selecting drag-coefficient values. Practical CFD utilization strategies necessary for the calibration of medium-to high-fidelity analysis tools are presented. Based on a comparative analysis of CFD simulations conducted at various time intervals, the results confirmed that under a certain time interval that sufficiently considers various factors, the accuracy of the FOWT response with respect to density shows minimal differences, thereby providing an efficient utilization method for CFD simulations in FOWT design and analysis.
Keywords:
Computational fluid dynamics, Floating offshore wind turbine, Time step, Middle-Fidelity engineering tool, Drag coefficient, Surge motion키워드:
전산유체역학, 부유식해상풍력, 시간단계, 중-정밀도 해석 도구, 항력계수, 서지 응답1. 서 론
해상 풍력 발전 기술의 발달은 지속 가능한 에너지원에 대한 전 세계적인 수요 증가와 함께, 최근 몇 년간 급속도로 진전되었다. 현재, 얕은 수심에서 경제적인 고정식 시스템이 해상풍력의 주류를 이루고 있는데, 더 넓은 영역의 해양공간을 활용하여 전력을 생산하기 위해 깊은 수심에서도 경제성을 확보할 수 있는 FOWT 연구가 많이 진행되고 있으며 이미 여러 선도적인 프로젝트를 통해 그 가능성이 증명되고 있다. 이러한 시스템 개발 과정에서, 초기 설계 및 규모 결정 단계에서는 주로 NREL에서 개발한 OpenFAST와 같은 단순화된 공학 모델인 중-정밀도 해석 도구를 사용하는 컴퓨터 시뮬레이션에 크게 의존하고 있다.[1] 그러나 이러한 접근법은 복잡한 해양 환경에서의 FOWT의 동적 행동을 정확히 예측하는 데 한계가 있음이 지적되어 왔다.
특히, 저주파 파동 여기와 응답의 중요성이 IEA Wind Task 30의 OC5 및 OC6 프로젝트를 통해 확인되었다.[2,3] 이러한 여기와 응답은 FOWT의 안전성 및 신뢰성에 중대한 영향을 미칠 수 있는데, 현재 널리 사용되는 중-정밀도 해석 도구들은 이를 상당히 과소평가하는 경향이 있다.[4~6] 이런 문제점을 파악하고 해당 연구에서는 포텐셜 흐름이론이 적용된 중-정밀도 해석 도구가 저주파 영역에서 발생하는 과소예측을 조정하기 위해서 2차 전달 함수(QTFs) 및 모리슨 항력계수를 적용함으로써 결과를 상당히 개선할 수 있었다.[2,3]
위와 같이, 모델을 개선하기 위해 사용되는 계수는 실험이나 CFD를 통해서 얻어지는데, 실험은 시간과 비용이 많이 들어가는 작업이므로 CFD를 이용한 방법이 경제적으로 더 유리하다. 많은 해양구조물 관련 연구자들이 극한 파도 상황에서 구조물의 응답을 연구하거나, 규칙파 조건에서 파도에 의한 움직임과 자유감쇠 움직임을 분석하기 위해 CFD 시뮬레이션을 활용하고 있다.[7~13] 그러나, 신뢰할 수 있는 결과를 얻기 위해서는 계산 격자의 크기 및 시간 단계를 충분히 작게 설정해야 하며, 이는 중-정밀도 해석 도구보다 훨씬 높은 계산 부하를 요구하게 된다. 따라서, 광범위한 매개변수 연구와 최적화 작업에 CFD를 단독으로 사용하는 것은 아직 현실적이지 않다. 대부분 경우, CFD는 실험의 대체로 사용되므로 계산 비용이 증가하더라도, 신뢰성을 높이기 위해 계산 격자 크기와 및 시간 단계 해상도를 높게 설정한다. 이 같은 설정은 단일 해석이나 해석 시간이 짧은 경우에는 문제가 없지만, 다양한 해양 환경조건에서 장시간에 걸쳐 비정상 해석을 요구하는 FOWT 수치해석에서는 한계가 있다. 중-정밀도 해석 도구를 보다 정밀하게 만들기 위해서는 환경조건에 따라 다른 계수를 적용해야 하는데, 이상적으로는 각기 다른 환경조건에 대해 CFD 해석을 통해 적절한 계수를 도출하는 것이 바람직하다. 그러나, 고해상도로 설정된 수치해석은 계산 자원과 시간의 제약 때문에 실제로 특정 비정규파 조건을 가진 몇 가지 대표적인 환경만을 선정하여 그 조건에서 해석을 수행하고 그 결과로부터 도출된 계수를 사용한다. 만약, 계산 비용과 시간 비용을 줄일 수 있다면 CFD를 특정 환경조건에서만이 아니라 더 많은 환경조건에서 활용할 수 있다. 상대적으로 낮은 해상도의 계산 격자 크기 및 시간 단계를 사용하면 계산비용과 시간 비용을 절감할 수 있다. 이 경우, 낮은 해상도로 수행된 CFD 해석이더라도, 해당 조건에서 얻은 해석 결과가 높은 해상도의 해석 결과와 비교하여 어느 정도 오차가 있는지 알고 있고, 그 오차가 허용범위 내에 있따면, 같은 비용으로 대표적인 환경조건 이외에도 더 많은 환경조건에서 CFD를 활용할 수 있을 것이다. 이러한 접근 방식은 CFD의 범용성을 확장하고, 리소스를 최적화하는 데 큰 도움이 된다.
본 연구는 CFD 계산 비용을 낮추기 위해 해상도를 낮추었을 때 나타나는 응답오차를 분석하였다. 해상도를 결정하는 대표적인 설정 변수에는 계산 격자 크기와 시간 단계 변수 중, 본 연구에서는 시간 단계 조정에만 초점을 맞추어 분석을 수행하였다. 특히, FOWT의 서지 방향 응답에 대한 분석을 진행하였고, 이와 관련하여 항력계수 결정에 초점을 두었다. 환경조건은 분석을 직관적으로 수행하기 위해 정규 파도 조건에서 시뮬레이션을 진행하였다. 그리고 기존의 연구들이 주로 DeepCwind 반잠수식 플로터와 같이 외부 칼럼과 중앙 칼럼이 명확히 분리된 구조를 대상으로 연구를 진행했던 것과는 달리, 본 연구에서는 외부 칼럼과 중앙 칼럼이 하부 폰툰으로 연결된 보다 복잡한 구조적 특성을 지닌 플로터를 사용하였다.
2. 연구 수행 방법 및 수치해석 설정
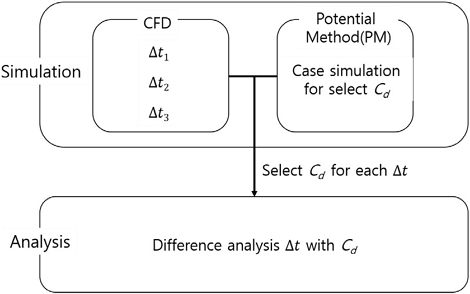
Fig. 1은 연구 수행 개략도를 나타낸 그림이다. 시간 단계 분석을 위해 상용 고-정밀도 해석 도구인 Star-CCM을 사용하여 총 3개의 시간 단계에 대한 해석을 수행하였다. 각 시간 단계는 Δt1, Δt2, Δt3로, 0.05s와 그 절반인 0.025s, 그리고 1/4값인 0.0125s로 설정하였다. 이 값들은 각각 Coarse Time-step(CT), Medium Time-step(MT), Fine Time-step(FT)으로 명명하였다. 각각의 시간 단계들을 적용한 CFD결과와 일치하는 항력계수를 도출하기 위해, 포텐셜 흐름 이론을 기반으로 하는 중-정밀도 해석 도구인 Orcaflex를 사용하여 해석을 수행하였다. 이후, 시뮬레이션을 통해 얻은 각 시간 단계별 항력계수 값에 대한 오차 분석을 수행하였다.
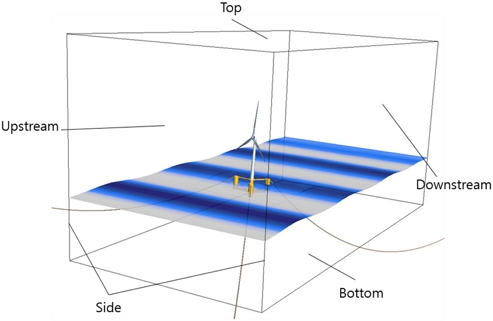
Fig. 2는 CFD를 수행하기 위해 설정한 수치 영역 설정을 나타낸 그림이다. Upstream, Bottom, Top 부분은 inlet velocity로 설정하였으며 Downstream은 outlet pressure로 설정하였고, Side는 symmetry로 설정하였다. 그리고 안정적인 수치해석을 위해 파도가 Downstream 경계에 닿기 200 m 전에 감쇠가 되도록 설정하였다.
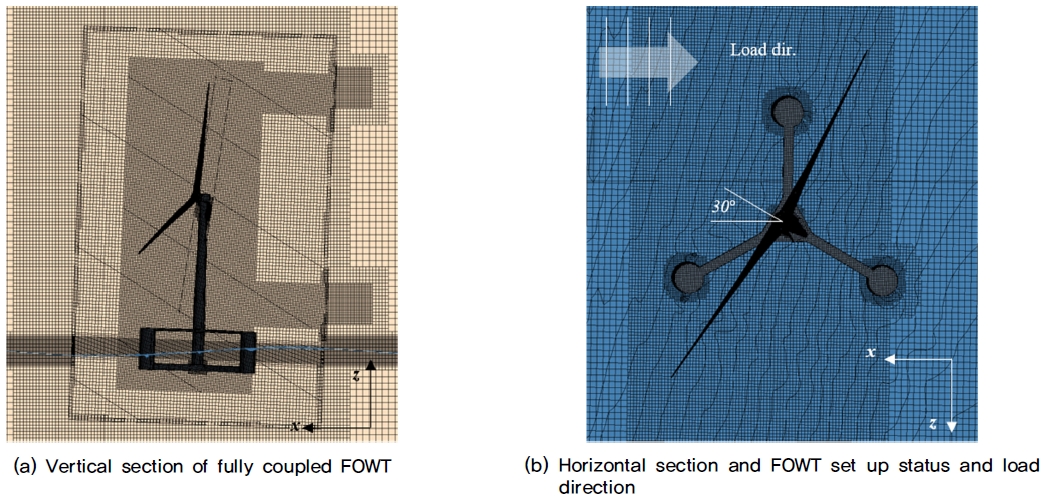
Fig. 3에서는 CFD 해석을 수행하기 위해 구성한 계산 격자 상태를 확인할 수 있다. Fig. 3a를 보면, 파도가 존재하는 영역과 FOWT가 존재하는 공간은 계산 격자를 더욱 조밀하게 구성하였다. 플로터와 해수면이 부딪히는 부분은 y+값이 5,000 이하가 되도록 하였으며 잠긴 부분은 2,000 미만에 되도록 계산 격자를 구성하였다. 또한, 시스템의 거동에 중요한 영향을 미치는 터빈의 경우, y+값이 200 이하가 되도록 계산 격자를 구성하였다.
Fig. 3b에서는 FOWT의 상태를 확인할 수 있는데 터빈이 바람 및 파도의 진행 방향과 수평을 이루지 않고 30° 비스듬한 방향이 되도록 하였다. 중-정밀도 해석 도구와 결과를 비교했을 때 더욱 극한의 상황을 연출하기 위해서 다음과 같이 터빈의 Yaw 각도를 변경하였고 풍속은 40.28 m/s, 파고는 8.34 m, 주기는 13.1 s, 해류는 0.77 m/s로 설정하였다. 이때 사용된 파동 스펙트럼 모델은 1st VoF 모델이 적용되었다. 난류모델로는 K-omega sst 모델이 사용되었다. 본 연구에서 사용된 난류모델은 비압축성 유체임을 가정하고, Navier-Stokes 방정식을 기반으로 하여 이산화하고 주어진 경계조건과 설정된 초기조건 하에서 수치적으로 계산하였다. CFD에서 난류는 다양한 시간 및 공간 스케일의 움직임을 포함하는 복잡한 현상이다. 이러한 복잡성 때문에 직접적인 계산은 어려운 경우가 많다. 이를 해결하기 위해 Navier-Stokes 방정식을 평균화하거나 필터링하여 난류에 의한 효과를 포함하는 수정된 방정식을 통해 해를 구하는 다양한 난류모델들이 개발되었다. 본 연구에서는 k-epsilon 모델과 k-omega 모델의 장점을 결합한 Shear Stress Transport(SST) 난류모델을 사용하였다. SST 난류모델에 대한 방정식은 다음과 같다.
Turbulent kinetic energy() 방정식:
| (1) |
Specific dissipation rate() 방정식:
| (2) |
여기서, Pt는 생성항, μt는 난류점성계수, σk,σw는 확산율, α,β,β*는 모델상수이다.
SST 모델은 특별한 혼합함수를 사용하여 k-epsilon 모델과 k-omega 모델 사이를 전환하게 되는데, 이를 통해 k-omega 모델의 벽 근처에서의 장점과 k-epsilon 모델의 벽에서 떨어진 영역에서의 장점을 모두 활용하게 된다.
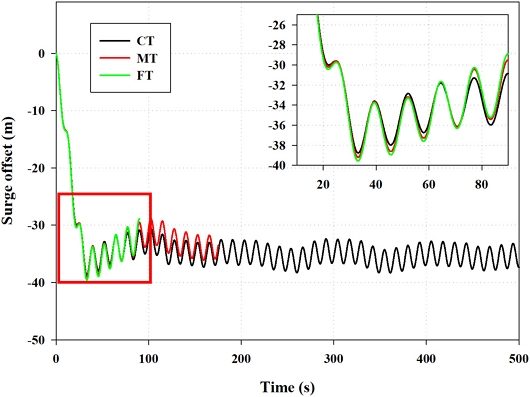
Fig. 4는 시간 단계에 따른 CFD 서지 응답 해석 결과를 나타낸 것이다. 시간 단계 해상도가 가장 낮은 CT의 경우, 하중 응답이 수렴되는 것이 충분히 확인되는 500s 구간까지 해석을 수행하였고, 동일한 CPU 시뮬레이션 시간을 적용하여 중간-시간 해상도인 MT와 고-시간 해상도인 FT는 각각 180s, 90s 동안 해석을 수행하였다.
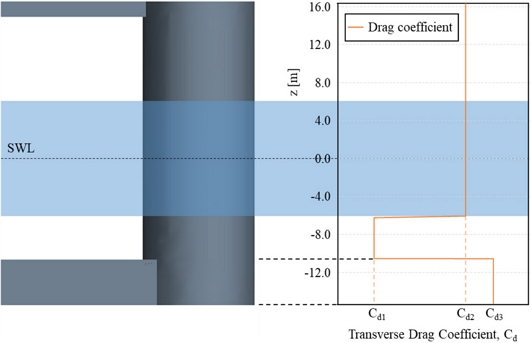
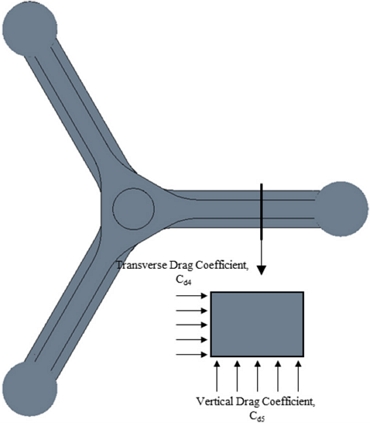
Fig. 5와 Fig. 6은 중-정밀도 해석 도구를 보정 하기 위해 항력계수를 적용한 것을 나타낸 그림이다. 칼럼 부는 파도의 영향이 없는 부분과 있는 부분, 그리고 폰툰과의 교차부에 할당할 항력계수를 각각 Cd1, Cd2, Cd3로 설정하였으며 여기서 Cd1, Cd2는 Wang et al.(2022)[13]에서 제시한 항력계수 값을 참고하여 적용하였다. 폰툰과 칼럼의 교차 부분에 적용할 항력계수 Cd3는 CFD 해석을 통해 얻어진 하중 응답 결과를 통해 결정하였다. Fig. 6에서는 폰툰에 할당하기 위한 Cd4, Cd5의 위치를 확인할 수 있는데, 각각 횡 방향과 수직 방향의 항력계수를 의미한다. 이번 연구에서는 서지 방향에 대해서 중점적으로 분석을 수행할 것이기에 수직 방향의 항력계수인 Cd5는 0으로 하고 고려하지 않았다. Cd4는 CFD 해석을 통해 얻어진 하중 응답 결과를 통해 결정하였다.
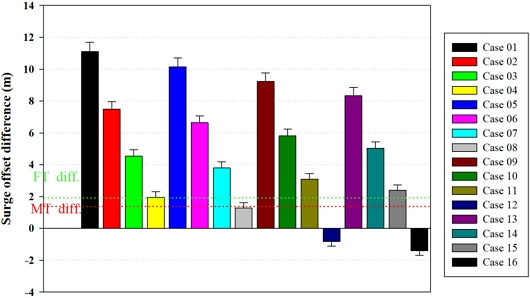
Cd3, Cd4 하중 응답 계수를 결정하기 위해서 Table 1과 같이 총 16개의 서로 다른 항력계수를 적용하여 중-정밀도 해석을 수행하였다. Cd3은 1부터 4까지 1 간격으로 항력계수 값을 구성하였으며 Cd4는 2부터 8까지 2 간격으로 항력계수 값을 구성하였다.
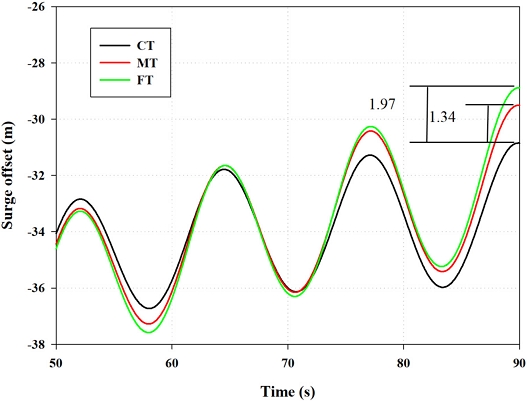
위와 같이 준비된 중-정밀도 해석 도구 시뮬레이션 결과를 CFD 서지 평균 응답 결과와 비교하여 CT, MT, 그리고 FT 시간 단계가 적용된 CFD 결과와 일치하거나 근접하는 결과가 나타난 항력계수 값이 적용된 케이스를 도출하였다. MT와 FT 시간 단계가 적용된 CFD결과는 CT 시간 단계가 적용된 CFD결과와 달리 중-정밀도 해석 도구 시뮬레이션과 비교할 수 있을 만큼 충분히 긴 해석이 수행되지 않았기 때문에 직접적인 비교가 어렵다. 그래서, MT와 FT 시간 단계가 적용된 CFD 결과와 일치하는 케이스를 도출하기 위해 Fig. 7과 같이 50 s에서 90 s 사이의 CFD 시계열 서지 하중 응답 결과 중 CT가 적용된 해석 결과와 가장 많이 차이가 나는 이격 값을 식별하였다. 이렇게 식별된 이격 값만큼 차이가 나는 결과와 일치하는 중-정밀도 해석 결과 값을 사용하여 MT와 FT 시간 단계가 적용된 CFD와 일치하는 항력계수 값으로 하였다. CT 시간 단계가 설정된 CFD 결과와 가장 많은 이격거리 차이가 발생한 구간은 90s로 확인되었으며 이때 MT 시간 단계가 적용된 CFD는 1.34 m, FT 시간 단계가 적용된 CFD는 1.97 m로 나타났다.
3. 결과 및 고찰
Fig. 8은 서로 다른 시간 단계를 적용하여 수행한 CFD의 수치적인 해의 불확정도를 확인할 수 있는 residual을 나타낸 그림이다. CT residual 결과를 살펴보면 수치적인 해가 충분히 수렴되지 않은 것으로 확인되었다. MT residual 결과는 CT 시간 단계가 적용된 해석 결과보다는 수치적인 해가 수렴되었지만, 수렴의 정도가 수치적인 해가 오차를 유발하지 않을 만큼 충분히 수렴되었다고는 할 수 있는 정도로 수렴하지는 않았다. FT residual을 살펴보면, 세 가지 시간 단계설정 중에서 수치적인 해가 가장 수렴했는데, Wang et al.(2021)[14]에서 언급된 바와 같이, 수치적인 해의 수렴 정도에 의해서 오차가 유발될 수 있는 확률을 무시할 수 있는 정도까지 수렴하지는 않았지만, 그에 준했기 때문에 FT 시간 단계가 적용된 해석은 충분히 수렴되었다고 판단하였다.
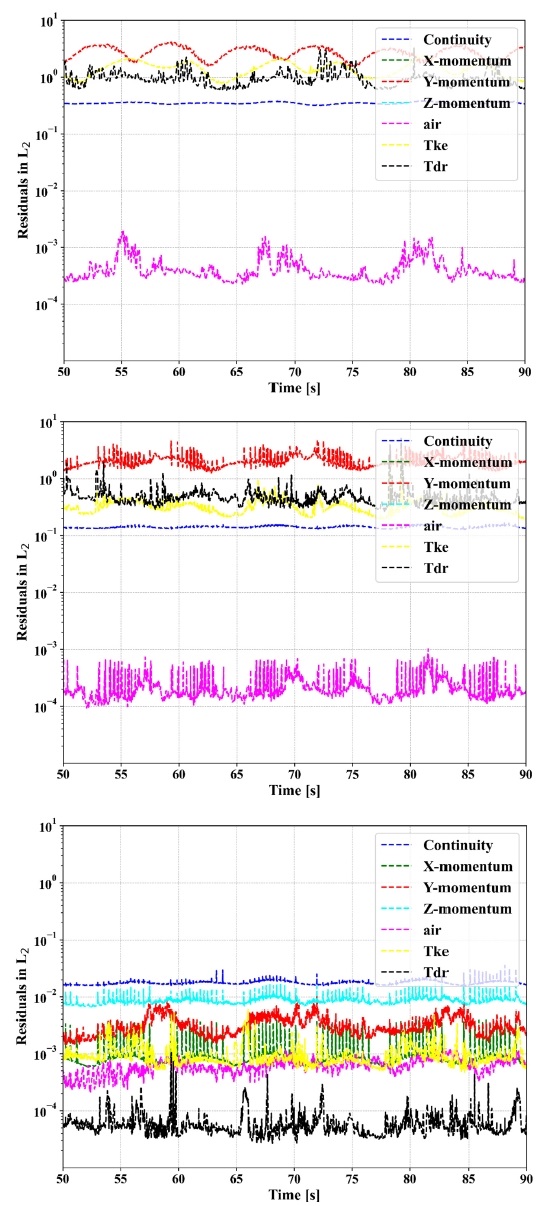
Simulation residual with time series (top : CT time-step adapted CFD result, middle : MT time-step adapted CFD result, bottom : FT time -step adapted CFD result)
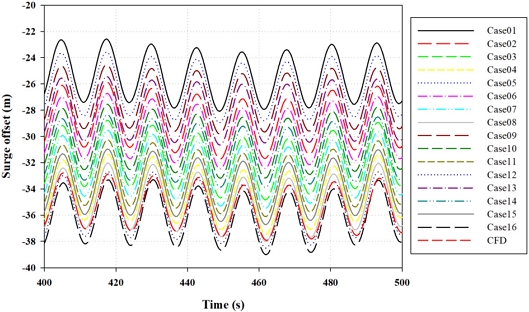
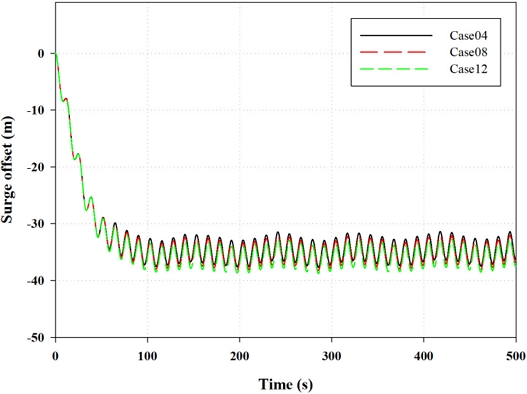
Fig. 9는 CT 시간 단계가 적용된 CFD해석 결과와 서로 다른 항력계수가 적용된 16개의 중-정밀도 통합하중해석 결과를 수행하여 그 중 서지 응답에 대해 시계열에 따라 비교한 그래프이다. 그래프를 통해 중-정밀도 해석 도구에 적용되는 항력계수 값에 따라서 주기와 응답 진폭은 차이가 거의 없지만 평균 응답은 차이가 나는 것이 확인되었다. Fig. 10은 CT 시간 단계가 적용된 CFD 서지 평균 응답 결과와 중-정밀도 시뮬레이션 서지 평균 응답 결과를 비교한 그래프이다. 여기서 MT와 FT 시간 단계가 적용된 CFD해석 결과는 Fig. 7에 나타나 있는 것처럼 각각 1.34 m 1.97 m 이격된 위치에 빨간색 점선과 초록색 점선으로 표시하였다. CT 시간 단계가 적용된 CFD는 Cd3가 3, Cd4가 8인 case12와 유사하게 나타났으며, MT 시간 단계가 적용된 CFD는 Cd3가 2, Cd4가 8인 case08와 거의 유사한 결과가 나타났으며, FT 시간 단계가 적용된 CFD는 Cd3가 1, Cd4가 8인 case04와 거의 유사한 결과가 나타났다.
하중 응답이 충분히 안정화된 결과를 가지고 분석을 수행해야 하는데, CT 시간 단계가 적용된 CFD의 경우, 충분히 안정화된 응답이 나타날 때까지 해석을 수행하였지만, 비용적인 한계로 인해 MT와 FT 시간 단계가 적용된 CFD는 충분한 해석을 수행하지 못하였다. 그래서, Fig. 11~13과 같이, 해당 CFD 결과와 유사한 서지 이격 차이를 보이는 중-정밀도 해석 도구의 하중 응답 결과를 대체로 사용하여 시간 단계에 따른 차이를 분석하였다.
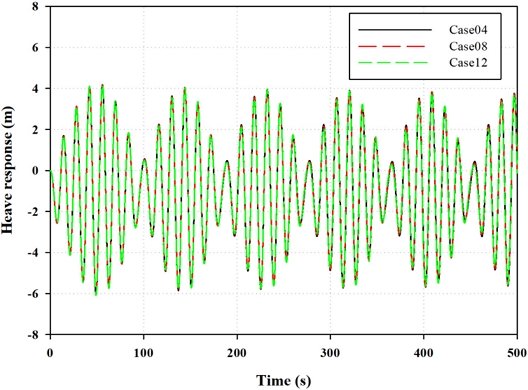
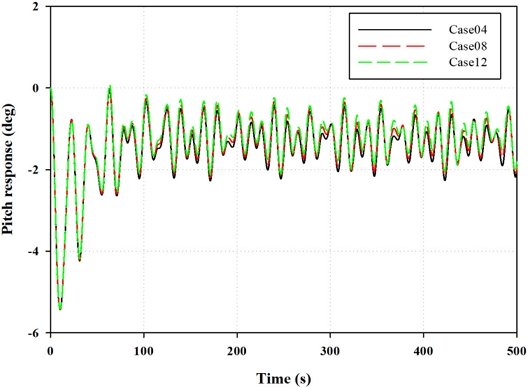
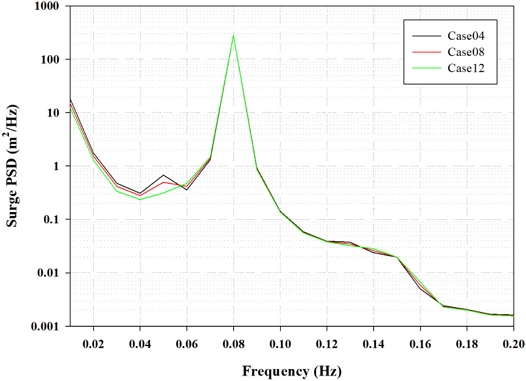
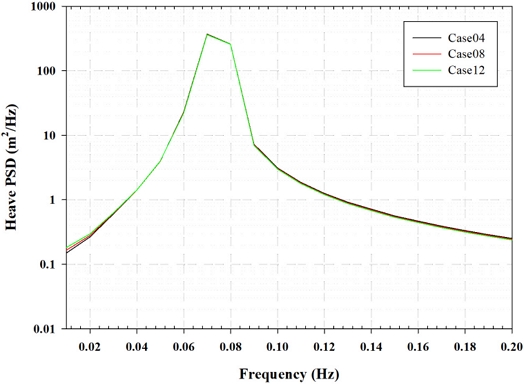
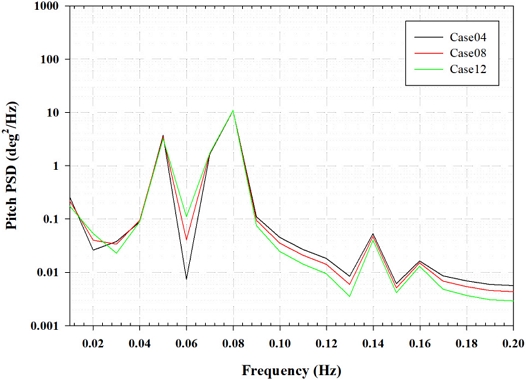
Fig. 11의 시계열 서지 응답을 살펴보면, CFD를 통해 확인된 응답 차이가 시스템이 안정화된 구간에서도 동일하게 나타난 것을 확인할 수 있다. 전체적인 응답은 극한 환경조건으로 인해 평균 서지 이격이 크게 나타났는데, 이 때문에 시간 단계에 따른 하중 응답의 차이가 크게 나타나지 않았다. Fig. 12에서는 시스템의 히브 응답을 확인할 수 있으며, 모든 시간 단계에서 동일한 응답이 관찰되었다. 그러나 피치 하중 응답 결과가 나타나 있는 Fig. 13에서는 시간 단계에 따라 피치 하중 응답에 일부 차이가 있음을 확인할 수 있었다. 주파수 응답을 비교하기 위해, 3 DoF 시계열 하중 응답 결과에 대한 PSD 주파수 분석을 수행하였다. Fig. 14의 서지 PSD 결과를 살펴보면, 파도 주파수 영역 부근인 0.08 hz부터는 시간 단계에 상관없이 모든 주파수 영역에서 잘 일치하는 모습이 보였다. 그러나 저주파 영역에서는 CT 시간 단계가 적용된 CFD와 유사한 결과를 가지는 case12에서 서지 PSD가 다소 낮게 나타났다. Fig. 15에서는 히브 PSD 결과를 확인할 수 있는데 파도 주파수 영역 범위에 상관없이 모든 시간 단계 해상도에서 결과가 일치하였다. 이는 서지 방향에 대한 항력계수 값이 히브 응답에는 거의 영향을 미치지 않았음을 보여준다. Fig. 16에서 피치 응답의 PSD 결과를 살펴보면, 파도 주파수 영역보다 큰 고주파 영역에서는 시간 단계 해상도가 낮은 경우에 다소 과소 예측되는 반면, 저주파 영역에서는 반대로 다소 과도 예측되었다.
Table 2에서 FT 시간 단계 CFD 결과와 일치하는 case04 결과를 기준으로 MT와 CT 시간 단계가 적용된 CFD 결과와 각각 일치하는 중-정밀도 해석 결과인 case08과 case12를 살펴보면, 평균 surge 방향 오차는 가장 낮은 해상도를 가지는 case12에서 3.45%의 적은 오차가 나타났다. 히브의 경우, 횡 방향의 항력계수 값에는 거의 영향을 받지 않는 것으로 확인되었고, 그에 반해 피치 평균 응답은 시간 단계 해상도가 낮아질수록 평균 응답이 다소 둔하게 나타나는 것이 확인되었으며 고-해상도 시간 단계에 비해 중-해상도 시간 단계 결과에서는 피치 평균 응답이 6.55%, 저-해상도 시간 단계 결과에서는 13.16% 낮게 나타났다. 하지만, 극한 환경조건임을 고려한 상태로 수치적인 부분으로 보았을 때, 고-해상도 시간 단계와 저-해상도 시간 단계의 평균 피치 응답 차이는 약 0.18°밖에 차이가 나지 않았다.
4. 결 론
본 연구는 CFD에 사용되는 시간 단계에 따른 FOWT 해석 결과를 분석하여 오차를 파악하고, 저 해상도 시간 단계가 적용된 CFD 결과의 신뢰성을 평가하였다. 또한, 시간 단계 해상도에 따라 다르게 결정된 항력계수 값들 간의 차이를 분석하여 그 영향을 측정하였다.
서지 방향 하중 응답에서 시간 단계 해상도가 낮을수록 저주파 영역에서의 PSD가 다소 낮게 나타나는데, 그 이유는 저 해상도로 인해 저주파수 영역에 대한 일부 하중을 포착하지 못했기 때문이라 판단된다. 또한 시간 단계 해상도가 낮을수록 하중이 다소 과도하게 해석되어서 서지 평균 응답이 다소 높게 나타났지만 작은 오차범위 내로 확인이 되어 본 연구에서 적용된 낮은 해상도의 시간 단계를 적용하여도 충분히 신뢰할만한 결과를 도출할 수 있는 것으로 확인되었다.
본 연구에서는 히브와 피치 하중 응답에 대해서 깊게 다루지는 않았지만, 중-정밀도 해석 도구에 횡 방향 항력계수를 적용한 결과, 히브 하중 응답에는 거의 영향을 미치지 않는 반면 피치 하중 응답에는 상당한 영향을 미치는 것을 확인하였다. 서지 방향에 대한 하중 응답은 시간 단계 해상도에 따라 Cd3 값이 1에서 3사이로, 상당히 넓은 허용범위를 가졌으며, 이러한 범위 내에서도 큰 차이가 발생하지 않았다. 이 결과를 바탕으로, 피치 하중 응답에서 발생할 수 있는 상당한 오차를 고려하여 최종 항력계수를 결정한다면, 모든 DoF에서 충분히 신뢰할 수 있는 항력계수를 결정할 수 있을 것으로 예상된다.
향후 연구에서는 시간 단계 해상도에 따른 히브와 피치 움직임의 차이가 적용되는 항력계수 간의 관계를 추가로 연구할 것이며, CFD를 효율적으로 활용할 수 있도록 계산 격자 크기에 관해서도 연구를 수행이 필요할 것으로 사료된다.
Subscript
| FOWT : | floating offshore wind turbine |
| CFD : | computational fluid dynamics |
| NREL : | national renewable energy laboratory |
| IEA : | international energy agency |
| QTFs : | quadratic transfer functions |
| CT : | coarse time-step |
| MT : | medium time-step |
| FT : | fine time-step |
| DoF : | degree of freedom |
| PSD : | power spectral density |
Acknowledgments
본 연구는 2024년도 산업통상자원부의 재원으로 한국에너지기술평가원의 에너지기술개발사업-신재생에너지핵심기술개발사업의 일환으로 수행되었습니다(과제번호 : 20213000000030).
References
-
Jonkman, J.M., 2013, “The new modularization framework for the FAST wind turbine CAE tool”, Proc. 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Grapevine.
[https://doi.org/10.2514/6.2013-202]

-
Robertson, A.N., Wendt, F., Jonkman, J.M., Popko, W., Dagher, H., Gueydon, S., Qvist, J., Vittori, F., Azcona, J., and Uzumoglu, E., et al., 2017, “OC5 Project phase II: validation of global loads of the deepcwind floating semisubmersible wind turbine”, Energy Procedia, 137, 38-57.
[https://doi.org/10.1016/j.egypro.2017.10.333]

-
Robertson, A.N., Gueydon, S., Bachynski, E., Wang, L., Jonkman, J., Alarcón, D., Amet, E., Beardsell, A., Bonnet, P., and Boudet, B., et al., 2020, “OC6 phase I: investigating the underprediction of low-frequency hydrodynamic loads and responses of a floating wind turbine”, J. Phys.: Conf. Ser., 1618, 032033.
[https://doi.org/10.1088/1742-6596/1618/3/032033]

-
Simos, A.N., Sparano, J.V., Aranha, J.A.P., and Matos, V.L.F., 2008, “2nd order hydrodynamic effects on resonant heave, pitch and roll motions of a large-volume semi-submersible platform”, Proc. ASME 2008 27th International Conference on Offshore Mehcanics and Arctic Engineering, 229-237.
[https://doi.org/10.1115/OMAE2008-57430]

-
Bayati, I., Jonkman, J., Robertson, A., and Platt, A., 2014, “The effects of second-order hydrodynamics on a semisubmersible floating offshore wind turbine”, J. Phys.: Conf. Ser., 524, 012094.
[https://doi.org/10.1088/1742-6596/524/1/012094]

-
Simos, A.N., Ruggeri, F., Watai, R.A., Souto-Iglesias, A., and Lopez-Pavon, C., 2018, “Slow-drift of a floating wind turbine: An assessment of frequency-domain methods based on model tests”, Renewable Energy, 116(Part A), 133-154.
[https://doi.org/10.1016/j.renene.2017.09.059]

-
Wu, G., Jang, H., Kim, J.W., Ma, W., Wu, M.-C., and O’Sullivan, J., 2014, “Benchmark of CFD modeling of TLP free motion in extreme wave event”, Proc. ASME 2014 33rd International Conference on Ocean. Offshore and Arctic Engineering, V002T08A086.
[https://doi.org/10.1115/OMAE2014-24658]

-
Pinguet, R., Kanner, S., Benoit, M., and Molin, B., 2021, “Modeling the dynamics of freely-floating offshore wind turbine subjected to waves with an open-source overset mesh method”, Proc. ASME 2021 3rd International Offshore Wind Technical Conference, V001T01A008.
[https://doi.org/10.1115/IOWTC2021-3536]

- Bozonnet, P., and Emery, A., 2015, “CFD simulations for the design of offshore floating wind platforms encompassing heave plates”, Proc. 25th International Ocean and Polar Engineering Conference.
- Sarlak, H., Pegalajar-Jurado, A., and Bredmose, H., 2018, “CFD simulations of a newly developed floating offshore wind turbine platform using OpenFOAM”, Proc. 21st Australasion Fluid Mechanics Conference.
-
Koop, A., Crepier, P., Loubeyre, S., Dobral, C., Yu, K., Xu, H., Zheng, Y., Kim, J., and Huang, J., 2021, “Development and verification of modeling practice for CFD decay calculations to obtain roll damping of FPSO”, Proc. ASME 2021 40th International Conference on Ocean, Offshore and Arctic Engineering, V008T08A030.
[https://doi.org/10.1115/OMAE2021-62411]

-
del ´Aguila Ferrandis, J., Bonfiglio, L., Rodríguez, R.Z., Chryssostomidis, C., Faltinsen, O.M., and Triantafyllou, M., 2020, “Influence of viscosity and non-linearities in predicting motions of a wind energy offshore platform in regular waves”, J. Offshore Mech. Arctic Eng., 142(6), 062003.
[https://doi.org/10.1115/1.4047128]

-
Wang, L., Robertson, A., Jonkman, J., and Yu, Y.-H., 2022, “OC6 phase I: Improvements to the OpenFASTpredictions of nonlinear, low-frequency responses of a floating offshore wind turbine platform”, Renewable Energy, 187, 282-301.
[https://doi.org/10.1016/j.renene.2022.01.053]

-
Wang, Y., Chen, H.-C., Vaz, G., and Mewes, S., 2021, “Verification study of CFD simulation of semi-submersible floating offshore wind turbine under regular waves”, Proc. ASME 2021 3rd International Offshore Wind Technical Conference, V001T01A010.
[https://doi.org/10.1115/IOWTC2021-3558]