태양에너지 시스템에 적합한 표준기상데이터의 제작과 일사량 데이터 분석
© 2017 by the The Korean Society for New and Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The typical meteorological year (TMY) data reflect the long-term meteorological characteristics in a specific location and thereby serve as critical input in solar energy simulations. On the other hand, domestically, only a few of studies have been dedicated to TMY data with reliable solar irradiance and their analysis. We generated new TMY data of 10 major cities using the meteorological data from 1991 to 2010 measured by the Korea Meteorological Administration (KMA). To generate TMY data suitable for solar energy systems, we applied a better solar decomposition model for direct normal irradiance (DNI) and the generation method by National Renewable Energy Laboratory (NREL). We analyzed the new TMY solar irradiance data by comparisons with the 20-year long-term means, data provided by Korean Solar Energy Society (KSES), and data included in the TRNSYS and PVsyst programs. Finally, we demonstrated that the TMY data proposed in this study represent the solar irradiance more appropriately.
Keywords:
Typical Meteorological Year Data, Solar Energy System, Solar Irradiance, Solar Radiation Model키워드:
표준기상데이터, 태양에너지 시스템, 일사량, 태양 복사 모델1. 서 론
태양광이나 태양열 시스템의 에너지 시뮬레이션에 있어서 기상 조건의 연간 변동성으로 인한 불확실성을 최소화하기 위해 장기간 기상특성을 반영할 수 있는 기상데이터의 활용이 중요하다.[1-4] 그래서 20년 이상 장기 기상데이터로부터 특정 지역의 기상특성을 정형화할 수 있도록 표준기상데이터를 제작하여 사용한다. 표준기상데이터가 향후 특정 기간의 기상 상태를 예측하거나, 특정 태양에너지 시스템의 실시간 성능을 예측하는데 적합한 것은 아니다. 하지만, 과거 데이터를 기반으로 특정 지역에서 가장 신뢰도 있는 기상 조건을 나타낸다는 점에서 TRNSYS[5], PVsyst[6], SAM[7] 등 태양에너지 시스템의 성능 시뮬레이션 프로그램에 널리 사용되고 있다.
표준기상데이터는 건구온도, 이슬점온도, 대기압, 풍속, 일사량 등 기상요소의 시간당 데이터를 포함하는 1년 동안의 데이터 패키지(기상요소마다 8760개 데이터)를 의미하며, 유럽에서는 TRY(Test Reference Year) 데이터, 미국에서는 TMY(Typical Meteorological Year) 데이터라 불린다.[1] 표준기상데이터는 표준기상월(TMM, Typical Meteorological Month)을 1월부터 12월까지 선정하고, 12개월 데이터를 연결하여 제작한다. 표준기상월은 장기간 기상특성이 잘 반영이 되도록 선정하는데, 선정 과정에서 건구온도, 풍속, 일사량 같이 중요한 기상요소에 가중치를 준다. 몇 가지 표준기상데이터 제작 방법이 있는데, 차이점은 주로 기상요소에 따른 가중치와 특정 월의 데이터가 보여주는 지속성을 판단하는 기준에 있다. 최근 태양에너지 분야에서는 미국 재생에너지연구소(NREL, National Renewable Energy Lab)를 중심으로 일사량에 높은 가중치를 주는 표준기상데이터 제작 방법이 널리 활용되고 있다.[3]
고정형 태양에너지 시스템의 시뮬레이션에는 태양광 패널이나 태양열 집열기에 조사되는 일사량, 즉, POA(Plane of Array) 또는 기울어진 표면 일사량이 필요하다.[8,9] POA 일사량은 수평면 전일사량(GHI, Global Horizontal Irradiance), 법선면 직달일사량(DNI, Direct Normal Irradiance), 수평면 산란일사량(DHI, Diffuse Horizontal Irradiance)으로 구성된다. 한편, 태양을 추적하는 집광형 태양에너지 시스템은 직달 성분만을 활용하기 때문에 시뮬레이션을 위해서는 DNI가 필수 불가결하다. 국내에서는 기상청(KMA, Korea Meteorological Administration)이 약 20개 지역의 일사량 측정값을 공개하고 있는데, GHI만 제공하고 DNI와 DHI는 제공하지 않는다.[10] DNI나 DHI를 측정하려면 고정밀도를 갖는 태양 추적 장치가 필요하기 때문에, 높은 설치비과 세밀한 유지관리로 인해 국내에서는 장기간 체계적으로 축적된 데이터가 많지 않다. 그래서 GHI를 직달과 산란 성분으로 분리하여 DNI와 DHI를 산출하는 직산분리 모델을 주로 사용한다.[8,9,11]
태양에너지 시스템의 전문 시뮬레이션 프로그램은 표준기상데이터를 라이브러리에 포함하고 있다. 하지만, 외국 프로그램이다 보니 국내 지역의 표준기상데이터를 많이 내장하고 있지는 않다 – TRNSYS는 6개 지역, PVsyst는 4개 지역, SAM은 2개 지역. 여기에 내장된 표준기상데이터는 월간 합의 일사량 데이터를 이용하여 적절한 모델링을 통해 시간별 데이터로 분할하여 제작하였다.[5-7] 월간 데이터도 지표면에서 실측보다는 위성 영상을 바탕으로 모델링을 통해 산출되었다.[12]
표준기상데이터의 부족을 극복하기 위해 국내에서도 관련 연구가 꾸준히 진행 되었다.[1,2] 하지만, 태양에너지 시스템에서 가장 중요한 일사량에 대한 상세한 분석이나 데이터가 많이 부족하다.[13] 기존 연구들은 GHI 위주로 일사량을 다루어왔기 때문에, DNI 데이터의 부족은 특히 심각하다. 또한, 실질적으로 공개된 표준기상데이터가 적기 때문에 사용자 입장에서 접근성이 매우 낮다. 90년대에 대한설비공학회에서 제공하였다가 중단한 이후로 현재는 한국태양에너지학회(KSES, Korean Solar Energy Society)[14]에서만 7개 도시의 표준기상데이터를 제공하고 있다.
본 연구의 목적은 태양에너지 시스템의 시뮬레이션에 활용에 적합하도록 일사량에 초점을 맞춘 표준기상데이터를 제작하고 분석하는데 있다. 기상청에서 제공하는 1991부터 2010년까지 20년간 데이터를 이용하여 국내 주요 10개 도시(부산, 청주, 대구, 대전, 강릉, 광주, 인천, 제주, 전주, 서울)의 표준기상데이터를 제작하였다. 선행 연구에서 Reindl et al.[15]의 두 번째 직산분리 모델이 국내에 적합한 것으로 평가되었기 때문에 이를 사용하여 GHI로부터 DNI를 계산하였다.[16] 표준기상데이터는 NREL의 제작방법을 적용하여 제작하였고, 제작한 표준기상데이터에서 일사량을 20년 장기 평균값, 공개된 KSES 데이터, TRNSYS 및 PVsyst의 전문 프로그램에 내장된 데이터와 비교 분석하였다.
2. 기상데이터와 법선면 직달일사량
표준기상데이터를 생성하기 위해서는 매시간 측정된 장기 기상 데이터가 필요하다. 기상청이 국내 100여개 지점에서 대기 온도, 풍속, 운량, 기압 등의 기상 데이터를 공개하고 있다.[10] 하지만, 기상청 데이터는 GHI를 포함하지만, DNI는 빠져있다. 외국에서도 DNI이 부재하는 경우는 많으며, 이럴 경우 DNI는 GHI를 이용하여 예측한다. 전일사량을 직달과 산란 성분으로 분리한다는 점에서 이런 종류의 복사 모델은 흔히 직산분리 모델로 부른다.[11]
일사량 직산분리 모델은 지역적 기후 특성을 반영하여 만들기 때문에, 특정 지역에서는 잘 맞지만 타 지역에서는 적합하지 않은 경우가 종종 있다. 국내에 적합한 직산분리 모델을 찾기 위해 선행연구[16]에서 Lee et al.[9], Reindl et al.[15]의 2개, Orgill and Hollands[17], Vignola and McDaniels[18], Louche et al.[19], Lam and Li[20], CIBSE[21], Erbs et al.[22], Maxwell[23] 등 전체 10개 모델을 비교 검토하였다. 한국에너지기술연구원이 대전(위도: 36.37, 경도: 127.37)에서 측정한 3년(2007∼2009) 간의 GHI와 DNI 쌍을 이용하였다. GHI는 Kipp & Zonen사의 CMP 11 센서로 측정하였고, 동일 회사의 SOLYS 2 태양 추적기에 장착된 CHP 1 센서로 DNI를 측정하였다. GHI와 DNI 모두 1분 간격 측정값을 평균하여 시간대별 데이터를 얻었다. 측정 값 중에서 태양 고도각이 5°이하인 경우와 GHI나 DNI 중에 하나라도 손실이 있는 경우를 제외하고, 전체 11,928개의 시간별 데이터 쌍을 활용하였다.
직산분리 모델의 적합성을 판단하는 기준으로 측정값에서 예측값을 뺀 평균경향오차(MBE, Mean Bias Error)와 평균제곱근오차(RMSE, Root Mean Square Error)를 계산하였다. Reindl의 2번째 모델과 Maxwell 모델을 제외한 다른 모델들은 DNI를 1,000W/m2 이상으로 과도하게 높게 예측하거나, 800W/m2 이상은 좀처럼 예측하지 못하는 비합리적인 경향을 보여주었다. 결과적으로 두 가지 모델 중에 Table 1에 정리된 바와 같이 MBE와 RMSE가 좋은 Reindl의 2번째 모델이 국내에 가장 적합하다고 결론 내렸다. 직산분리 모델의 비교 및 검토에 대한 자세한 내용은 선행연구에 정리되어 있다.[16] 본 연구에서는 Reindl의 2번째 모델을 DNI 산출에 적용하여 표준기상데이터를 제작하였다. 참고로 선행연구에서 Maxwell 모델을 기반으로 Reindl의 2번째 모델보다 개선된 예측능력을 갖는 새로운 직산분리 모델을 개발하였다. 하지만, 대전지역 3년간 데이터로만 개발했기 때문에, 표준기상데이터의 공공성을 감안하여 오랜 기간 동안 많은 지역에서 검증 후 사용되어야 한다고 판단해서 본 연구에 적용하지 않았다.
3. 표준기상데이터 제작 방법
표준기상데이터 제작의 선행 조건은 앞에서 언급한 바와 같이 장기간 축적된 기상 데이터이다. 이를 이용하여 표준기상월을 1월부터 12월까지 선정하고, 12개월 데이터를 연결하여 가상적인 표준기상데이터를 제작한다. 표준기상월을 선정하는 방법은 여러 가지가 있는데,[1] 본 연구에서는 Sandia 방법에 기반을 둔 미국 재생에너지연구소 NREL의 TMY 데이터 제작 방법을 이용하여 국내 지역의 표준기상데이터를 제작하였다.[3]
Sandia 방법은 1978년 Sandia Lab의 Hall이 고안하였는데, 원래 9가지 기상요소를 사용하였다. NREL은 Sandia 방법을 근간으로 DNI를 추가하여 10가지 기상요소로 표준기상데이터를 제작한다. 수평면 전일사량과 법선면 직달일사량에 대해서는 일간 합을, 건구 온도와 이슬점 온도에 대해서는 일간 최대, 최소, 평균을, 풍속에 대해서는 일간 최대, 평균을 고려한다. 표준기상월 선정 할 때, 기상요소의 가중치, 데이터 포맷 등에 따라 표준기상데이터의 버전이 다른데, NREL은 가장 최근 버전을 TMY3 데이터로 명명하고 있다. 각 기상요소에 대한 가중치는 Table 2에 정리하였다. 가중치를 보면 원래 Sandia 방법에 비해 NREL의 현재 방법은 풍속에 대한 가중치가 줄었고, DNI에 대한 가중치가 새로 도입되었다. GHI와 DNI를 합하여 일사량의 가중치가 전체의 50%를 차지한다. 참고로 CIBSE 방법을 보면, DNI는가중치가 없고 GHI만 1/3로 주어진다.[1]
NREL 표준기상데이터 제작 절차를 요약하면 다음과 같다. 단계 1에서는 Table 2의 10개 기상요소 항목별로 누적분포함수(CDF, Cumulative Distribution Function)가 장기에 근접한 순서로 5개 후보월을 선정한다. 각 항목별로 측정 기간 전체의 장기 누적분포함수와 특정년도의 월에 대해 단기 누적분포함수를 계산한다. Finkelstein-Schafer (FS) 통계라 부르는 값을 이용하여 장기 누적분포함수와 단기 누적분포함수의 차이를 근거로 근접성 순위를 매긴다.[24]
| (1) |
여기서 δi은 특정 기상요소 값에서 장기 누적분포함수와 단기 누적분포함수의 절댓값 차이이며, n은 계산하는 월의 데이터 개수이다. 10개 기상요소에 대해 FSj 값을 각각 구하고 Table 2의 가중치 wj를 곱해서 아래와 같이 가중치 합을 구한다.
| (2) |
단계 2는 단계 1에서 선정한 5개 후보월 중에서 평균과 중앙값 기준으로 장기 데이터에 가까운 순서대로 순위를 정한다. 기상 요소 중에서 건구 온도 평균값과 GHI에 대해서만 적용한다.
단계 3은 지속성을 평가한다. 건구 온도 평균값에 대해서 67 백분위 수 보다 높은 데이터와 33 백분위 수 보다 낮은 데이터의 발생 빈도와 연속 발생일 수를 계산한다. GHI에 대해서는 33 백분위 수 보다 낮은 날의 수를 계산한다. 가장 길게 발생하거나, 가장 여러 번 발생하거나, 한 번도 발생하지 않는 달은 제외한다. 결과적으로 단계 2에서 결정된 근접성 순서가 높은 월 중에 지속성 평가를 통과한 월을 표준기상월로 선정한다. 요약하면, 표준기상월은 Table 2의 가중치를 반영한 기상요소들을 기준으로 평균과 분포가 장기 값과 가장 가까우면서 특이한 기상현상이 발생한 월을 제외하고 선정한다.
단계 4는 선택한 12개 표준기상월을 연결하여 표준기상데이터를 제작한다. 연결 시, 월간 접점에서 발생하는 불연속성을 제거하기 위해 6 시간 전후 데이터는 선형보간 하여 사용한다.
이와 같은 방법으로 제작한 표준기상데이터를 태양에너지 시뮬레이션 프로그램인 TRNSYS[5]와 PVsyst[6]에 내장된 표준기상데이터를 비교할 예정이다. 위 프로그램에서 제공하는 표준기상데이터는 측정값을 바탕으로 제작되지 않았다. TRNSYS 표준기상데이터는 Meteonorm 사에서 제공하였다[5]. Meteonorm 데이터는 전세계 지역의 기상데이터를 제공하는데, 측정값이 없는 지역은 주변 지역의 기상데이터를 바탕으로 월간 평균값을 추정한다[12]. 월간 평균값을 이용하여 일간, 시간별 데이터를 확률적으로 생성한다. 표준기상데이터는 본 연구와 유사하게 NREL의 TMY 데이터 제작 방법을 활용한다. PVsyst도 아시아 지역에 대해서는 Meteonorm의 월간 데이터를 사용한다[6]. 그리고 자체적으로 내장된 알고리즘을 사용하여 시간별 데이터를 만든다.
4. 표준기상데이터 분석
위에서 요약한 NREL의 표준기상데이터 제작 방법을 프로그램으로 제작하였고, 부산, 청주, 대구, 대전, 강릉, 광주, 인천, 제주, 전주, 서울 국내 주요 10개 도시의 표준기상데이터를 생성하였다. 주요 도시는 전국적으로 고른 지역적 분포가 되도록 선정하였다. 1991부터 2010년까지 20년 동안, 기상청에서 제공하는 기상데이터를 사용하였다.[10]
Table 3은 각 지역에서 선정된 표준기상월을 보여주고 있다. 본래 Sandia 방법과 유사하게 DNI를 고려하지 않고 GHI만 가중치 10/20을 고려해서 표준기상데이터를 생성했을 때, 몇몇 지역에서 표준기상월이 바뀌는 경우가 발생한다. 하지만, 대부분의 경우에서 표준기상월이 1개정도 바뀌거나 전혀 바뀌지 않았다. DNI 고려 여부가 표준기상월 선정에 큰 영향을 안 준다고 볼 수도 있고, DNI가 GHI 데이터로부터 직산분리 모델을 통해 얻어졌기 때문에 상관성이 존재하는 것으로 볼 수도 있다. 그럼에도 불구하고 태양에너지를 활용하는 측면에서 보면, DNI 데이터 자체에 대한 필요성이 있기 때문에 표준기상데이터에 DNI를 포함하는 것은 바람직하다. 따라서, NREL 방법처럼 DNI와 GHI에 같은 가중치를 주는 것이 태양에너지 시스템에 합리적이라 판단된다.
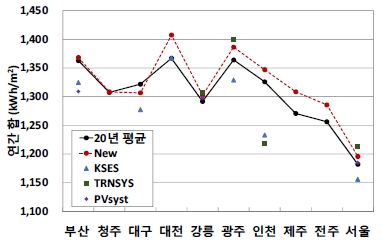
Fig. 1은 10개 도시의 연간 GHI 합을 보여준다(데이터는 Table 4에 정리하였다). 신규 표준기상데이터의 GHI가 20년 장기 평균값보다 다소 높은 경향을 보이는데, 차이가 3% 이내로 표준기상데이터의 불확도[25]를 감안하면 장기 평균을 잘 추종한다고 볼 수 있다. 반면에 KSES 데이터는 장기 평균 대비 전반적으로 작다. KSES 데이터에서 인천의 GHI값만 장기 평균값 대비 7.0% 작아서, 가장 큰 차이를 보이고 있다. 인천을 제외한다면, 장기 평균값 대비 KSES 데이터의 차이도 약 3.0%정도로 작게 된다. 이는 신규 데이터가 보여주는 차이와 크게 구별되지 않기 때문에 KSES와 신규 데이터 모두 GHI 관점에서는 합리적인 범위 내에서 변한다고 볼 수 있다. 공교롭게도 TRNSYS의 GHI값 역시 인천에서 차이가 가장 커서 장기 평균 보다 8.1% 작다. 하지만, 이를 제외한다면 TRNSYS와 PVsyst도, 신규 및 KSES 데이터와 동일하게, 3% 이내에서 변하는 연간 GHI값을 나타낸다.
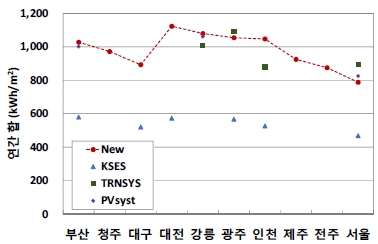
Fig. 2는 연간 DNI 합을 보여준다. DNI는 실측 데이터가 없으므로 신규 표준기상데이터를 기준으로 비교해 보자. PVsyst의 데이터는 상당히 잘 일치한다. 서울에서 –4.8% 차이이지만, 부산과 강릉은 3% 이내의 차이이다. TRNSYS는 서울과 인천에서 15% 정도의 차이이고, 강릉과 광주에서 차이는 7% 이내이다. 이와 달리 KSES 데이터에서 DNI의 차이는 확연히 드러난다. KSES의 연간 DNI는 6개 도시 전체에서 600kWh/m2을 넘지 않고, 신규 데이터 대비 50%도 되지 않는다. 시간별 데이터를 살펴보면, 1년 내내 DNI의 최댓값도 700W/m2을 넘는 경우가 거의 없다. 하지만, 국내에서도 맑은 날에 직달일사량계로 측정하면, DNI가 자주 800W/m2을 넘는 것을 관찰할 수 있다. KSES의 DNI는 Lee et al.[9] 모델을 이용한 것으로 추측되는데, 선행연구에서 보듯이 KSES의 DNI는 Lee et al.[9] 모델과도 큰 차이를 보이고 있다. KSES 데이터에서 큰 차이가 발생하는 원인이 명확하지 않다.
한편, Table 4에는 연간 DHI 합도 같이 정리하였다. 참고로 KSES 데이터에는 DHI가 포함되어 있지 않다. 신규 표준기상데이터와 전문 프로그램의 데이터를 비교하면, 강릉을 제외하고 나머지 지역에서는 TRNSYS나 PVsyst가 5% 이내의 차이를 보인다. 결론적으로, 몇몇 도시에서 예외적으로 큰 차이가 존재하지만, GHI, DNI, DHI의 연간 일사량 관점에서 신규, TRNSYS, PVsyst 표준기상데이터는 유사한 경향을 나타낸다.
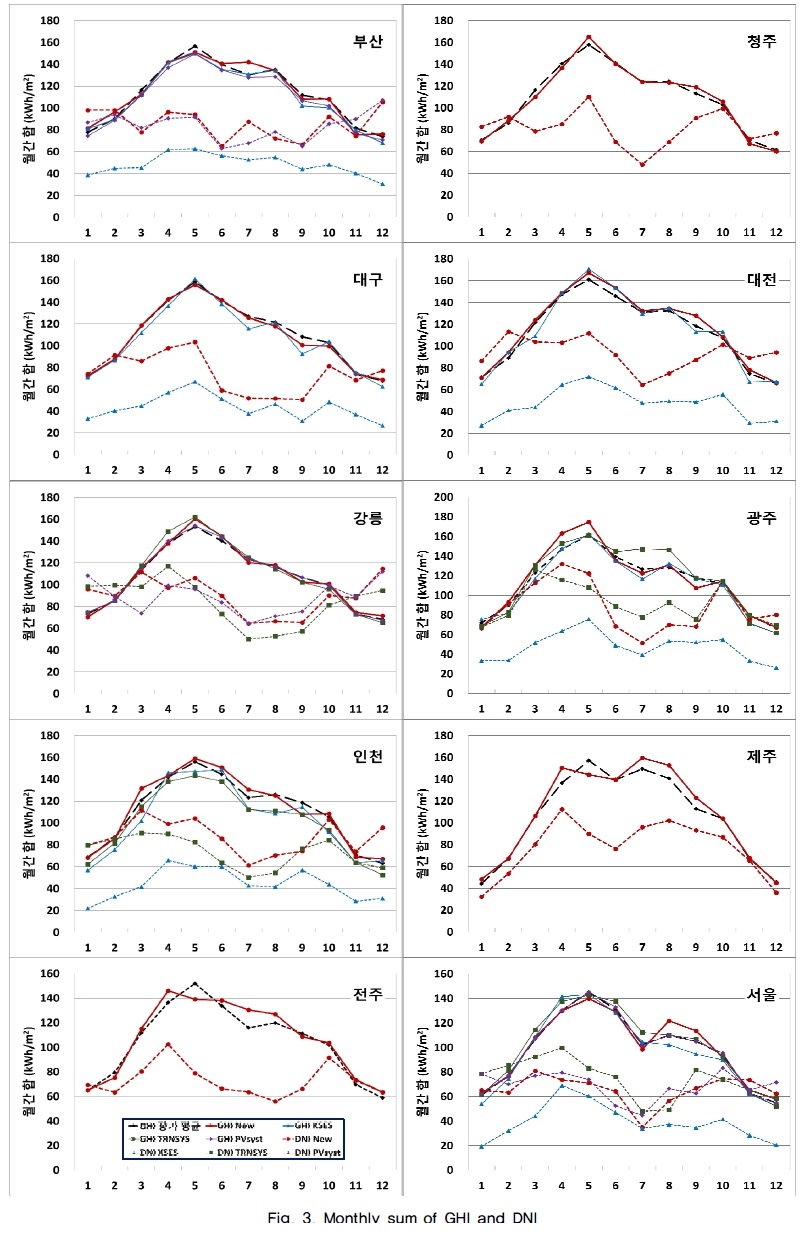
Fig. 3은 GHI와 DNI의 월간 합 분포를 보여준다. 우선 GHI부터 살펴보면, 신규, KSES, TRNSYS, PVsyst 모두 장기 평균값과 유사하다. 표준기상데이터 선정을 위해 사용하였던 NREL의 방법 자체가, 특정 지역에서 장기 평균과 가까운 5개 후보월이 선정된 다음 특이한 특성을 보여주는 월을 제외하는 방식이다. 따라서, 특이한 기상 특성을 보이지 않으면서 장기간의 월평균을 가장 잘 추종하는 월들을 연결하면 표준기상데이터가 된다고 볼 수 있다. 본 논문에서는 일사량에 대해서만 보여주었지만, 다른 기상요소 역시 장기 평균값과 큰 차이를 보이지 않고 있다.
조금 더 세밀한 검토를 위해 월간 합 12개 값을 이용하여 평균경향오차 MBE와 평균제곱근오차 RMSE를 계산하여 Table 5에 정리하였다. 오차는 장기 평균값에서 각 표준기상데이터의 값을 뺀 것으로 정의하였다. Fig. 1의 연간 GHI 합 변화와 일치하여, 신규 데이터의 MBE는 음수 값으로 KSES 데이터의 MBE는 양수 값으로 나타나는 경향을 보인다. 대전을 제외한다면, MBE의 절대값은 신규 데이터가 KSES 데이터보다 작다. 즉, 신규 데이터의 월간 GHI 합이 장기 특성에 보다 가깝다. 낮은 RMSE 값도 동일하게 신규 데이터의 적합성을 증명하고 있다. TRNSYS의 MBE와 RMSE를 비교하더라도, 신규 데이터의 MBE와 RMSE가 더 좋다. 흥미롭게도 PVsyst와 비교하면, 부산만 신규 데이터가 더 좋다. PVsyst에서 강릉과 서울의 MBE와 RMSE는 신규 데이터보다 더 좋을 뿐만 아니라 장기 평균에 매우 근접해서 놀라울 정도이다.
DNI를 살펴보면, 신규와 KSES 데이터의 차이는 Fig. 2의 연간 합보다 더 극명하다. 모든 도시에 걸쳐서 월간 DNI 합의 차이는 최대 70%까지 늘어난다. 특히, KSES 데이터에서 겨울철 DNI는 매우 작아서 전반적인 DNI 변화 특성에서 벗어난다. 신규, TRNSYS, PVsyst 데이터는 겨울철 DNI가 여름과 유사하거나 서울이나 강릉처럼 오히려 증가하기도 한다. 하지만, KSES의 DNI는 분포는 GHI와 유사해서 겨울철이 여름보다 일관성 있게 낮다. 한편, 신규 데이터와 TRNSYS, PVsyst를 비교하면, 연중 어느 정도 유사하게 변하는 추세는 확인할 수 있으나, 특정 월마다 DNI 차이는 최대 약 40% 범위에서 불규칙으로 나타난다. 그럼에도 불구하고, 부산, 광주, 서울에서 차이는 작은 편이고, 특히 PVsyst가 TRNSYS 보다는 신규 데이터와 더 일치하는 경향을 보인다. 이와 같은 정성적인 경향을 정량적인 비교 결과로 만들기 위해서는 DNI 변동성이 보다 줄어들어야 한다. DNI에서 보여주는 변동성은 신규 데이터에서 직산분리 모델링과 TRNSYS와 PVsyst에서 월간 데이터를 시간 데이터로 분할하는 과정에서 발생하였다. 변동성을 줄이기 위해서는 모델을 개선하는 노력과 함께 신뢰도 높은 실측 데이터의 축적이 필요하다.
그림으로 보여주지는 않았지만, 신규, TRNSYS, PVsyst 데이터의 월간 DHI 합을 비교해 보면 Fig. 3의 GHI와 유사한 수준에서 서로 잘 일치하고 있다. GHI와 DHI와 달리 DNI만 큰 오차를 드러내는 것은 DNI의 측정과 분석의 어려움을 재확인 해준다. GHI와 DHI는 수평면 위에서 모든 각도로 들어오는 일사량 전체를 나타내는 반면에, DHI는 직달일사량계에서 2.5°이하의 좁은 수광각을 통해 들어오는 직진 성분의 일사량만을 측정해야 하므로 어려울 수밖에 없다. 그리고 먼지 같은 대기의 상태에 민감하고, 태양의 고도각이 낮아지면서 공기 입자의 산란의 영향이 커지기 때문에 변동성이 커진다.
지금까지의 비교 결과를 종합해 보면, 신규, TRNSYS, PVsyst 데이터는 전반적으로 일치하는 일사량을 보여준다. 반면에, KSES 데이터는 GHI는 일치하지만, DNI는 교정이 필요하다. 표준기상데이터의 출처에 따라 DNI의 변동성이 큰 것을 확인하였는데, 변동성이 태양에너지 시스템의 성능에 주는 영향은 별도로 검토해야 한다. 고정형 태양에너지 시스템은 직달일사량뿐만 아니라 산란일사량도 활용하기 때문에 패널의 설치각도와 종류에 따라 표준기상데이터의 DNI 변동성이 다소 줄어들 수도 있다. 집광 기반의 태양에너지 시스템은 DNI가 그대로 입력 일사량이 되므로, 표준기상데이터에서 DNI가 갖는 변동성이 생산량 예측의 변동성에 바로 반영될 것이다.
본 연구는 기상청에서 GHI를 측정한 10개 도시에 대해 표준기상데이터를 제시하고 있다. Table 3을 보면 최저 지역 서울 대비 최고 지역 대전의 일사량은 약 18%정도 높다. 타 지역에 대한 표준기상데이터를 제작하여 국내 일사량 분포를 파악할 필요가 있다. 기상청에서 측정한 GHI가 있는 지점은 이를 활용하고, 없는 지점은 GHI를 모델링하거나[27,28] 주변 지역 정보를 바탕으로 추정해서 국내 지역의 표준기상데이터를 지속적으로 제작할 계획이다. 많은 지점의 표준기상데이터 제작과 분석을 통해 일사량 데이터의 누적 및 갱신은 향후 태양에너지 기술의 연구와 보급에 기초 자료로 널리 활용될 수 있을 것이다.[29,30]
5. 결 론
본 연구는 태양에너지 시스템의 시뮬레이션에 보다 적합하도록 일사량에 초점을 두고 국내 주요 10개 도시의 표준기상데이터를 제작하였고, 일사량을 중심으로 데이터를 분석하였다. 기상청의 20년간(1991~2010) 데이터를 기반으로 NREL의 표준기상데이터 제작방법과 Reindl의 두 번째 직산분리 모델을 적용하였고, 결론은 다음과 같다.
- 1)연간 GHI 합은 신규, KSES, TRNSYS, PVsyst 데이터 모두 20년 장기 평균값 대비 3% 이내에서 전반적으로 잘 일치하였다.
- 2)신규 데이터의 연간 DNI 합을 기준으로 비교하면, PVsyst는 5% 이내, TRNSYS는 15% 이내에서 일치하였다. 하지만, KSES 데이터는 50% 이하로 매우 낮았기 때문에 데이터에 대한 재검토가 필요하다.
- 3)신규, KSES, TRNSYS, PVsyst 데이터 모두 장기 평균과 유사한 월간 GHI 합의 분포를 보였다. 신규 데이터의 MBE와 RMSE가 전반적으로 가장 낮기 때문에 본 연구에서 제시한 표준기상데이터가 태양에너지 시스템에 보다 적합하다.
- 4)월간 DNI 합에서 신규, TRNSYS, PVsyst 데이터 사이에는 일관성 있는 분포와 상대적 유사성이 존재한다. 하지만, 높은 변동성으로 인해 최대 40%까지의 차이가 발생하였고, 지속적으로 변동성 감소의 노력을 통해 보다 정량적인 분석이 필요하다.
- 5)본 연구의 결과는 에너지 시뮬레이션에 신뢰할만한 일사량 데이터를 제공할 뿐만 아니라 유효참조표준데이터[26]로 등록되어 활용될 예정이므로 데이터의 제작과정 및 유용성을 검토한다는 점에서도 의의가 있다.
Nomenclature
| DHI : | Diffuse Horizontal Irradiance |
| DNI : | Direct Normal Irradiance |
| GHI : | Global Horizontal Irradiance |
| KSES : | Korean Solar Energy Society |
| MBE : | Mean Bias Error |
| NREL : | National Renewable Energy Lab |
| RMSE : | Root Mean Square Error |
| TMY : | Typical Meteorological Year |
Acknowledgments
본 연구는 산업통상자원부의 표준화기술개발사업(B6-7601)과 교육부 한국연구재단(2016R1A2B4012875)의 지원으로 수행한 연구과제의 결과입니다.
References
-
Yoo, H.C., Park, S.H., (2014), “Comparative analysis of diverse typical weather data model for building energy assessment”, J. Architec. Inst. Korea, 30(3), p215-222.
[https://doi.org/10.5659/jaik_pd.2014.30.3.215]

-
Lee, K., Yoo, H., Levermore, G.J., (2010), “Generation of typical weather data using the ISO test reference year (TRY) method for major cities of South Korea”, Energy Build, 45(4), p956-963.
[https://doi.org/10.1016/j.buildenv.2009.10.002]

- Wilcox, S., Marion, W., (2008), “Users manual for TMY3 data sets”, NREL/TP-581-43156, NREL, Golden, CO, USA.
-
Sengupta, M., Habte, A., Kurtz, S., Dobos, A., Wilbert, S., Lorenz, E., Stoffel, T., Renné, D., Gueymard, C.A., Myers, D., (2015), “Best practices handbook for the collection and use of solar resource data for solar energy applications”, TP-5D00-63112, NREL, Golden, CO, USA.
[https://doi.org/10.18777/ieashc-task46-2015-0001]

- TRNSYS, http://www.trnsys.com, .
- PVsyst, http://www.pvsyst.com/en/, .
- SAM (System Advisor Model), https://sam.nrel.gov/, .
- Duffie, J.A., Beckman, W.A., (2013), “Solar engineering of thermal processes”, 3rd ed., John Wiley & Sons, NJ, USA.
-
Lee, K., Yoo, H., Levermore, G.J., (2013), “Quality control and estimation hourly solar irradiation on inclined surfaces in South Korea”, Renew. Energy, 57, p190-199.
[https://doi.org/10.1016/j.renene.2013.01.028]

- Korea Meteorological Administration (KMA), https://data.kma.go.kr/cmmn/main.do, .
- Wong, L., Chow, W., (2001), “Solar radiation model”, Appl. Energy, 69(3), p191-224.
- Meteonorm, http://www.meteonorm.com/, .
- Yoo, H.-C., Lee, K.-H., Kang, H.-G., (2009), “Comparative analysis of the global solar horizontal irradiation in typical meteorological data”, J. Korean Sol. Energ. Soc, 29(6), p102-109.
- Korean Solar Energy Society (KSES), http://www.kses.re.kr/data_06/list_hi.php, .
-
Reindl, D.T., Beckman, W.A., Duffie, J.A., (1990), “Diffuse fraction correlations”, Sol. Energy, 45(1), p1-7.
[https://doi.org/10.1016/0038-092x(90)90060-p]

-
Lee, H.-J., Kim, S.-Y., Yun, C.-Y., (2017), “Comparison of solar radiation models to estimate direct normal irradiance for Korea”, Energies, 10(5), p594.
[https://doi.org/10.3390/en10050594]

-
Orgill, J., Hollands, K., (1977), “Correlation equation for hourly diffuse radiation on a horizontal surface”, Sol. Energy, 19(4), p357-359.
[https://doi.org/10.1016/0038-092x(77)90006-8]

-
Vignola, F., McDaniels, D., (1986), “Beam-global correlations in the Pacific Northwest”, Sol. Energy, 36(5), p409-418.
[https://doi.org/10.1016/0038-092x(86)90088-5]

-
Louche, A., Notton, G., Poggi, P., Simonnot, G., (1991), “Correlations for direct normal and global horizontal irradiation on a French Mediterranean site”, Sol. Energy, 46(4), p261-266.
[https://doi.org/10.1016/0038-092x(91)90072-5]

-
Lam, J.C., Li, D.H., (1996), “Correlation between global solar radiation and its direct and diffuse components”, Build. Environ, 31(6), p527-535.
[https://doi.org/10.1016/0360-1323(96)00026-1]

- CIBSE Guide J, (2008), “Weather, solar and illuminance data”, Chartered Institution of Building Services Engineers.
-
Erbs, D., Klein, S., Duffie, J., (1982), “Estimation of the diffuse radiation fraction for hourly, daily and monthlyaverage global radiation”, Sol. Energy, 28(4), p293-302.
[https://doi.org/10.1016/0038-092x(82)90302-4]

- Maxwell, E.L., (1987), “A quasi-physical model for converting hourly global horizontal to direct normal insolation”, SERI/TR-215-3087, Solar Energy Research Institute, Golden, CO, USA.
-
Finkelstein, J.M., Schafer, R.E., (1971), “Improved goodness-of-fit tests”, Biometrika, 58, p641-645.
[https://doi.org/10.2307/2334400]

-
Kim, S., Lee, H., Kim, H., Jang, G., Yun, C., Kang, Y., Kang, C., Choi, J., (2016), “A study on uncertainty to direct normal irradiance of typical meteorological year data”, New & Renew. Energy, 12(S2), p36-43.
[https://doi.org/10.7849/ksnre.2016.10.12.s2.36]

- National Center for Standard Reference Data (NCSRD), http://www.srd.re.kr/main/page.do, .
-
Kim, H., Kim, J., (2016), “Correlation to predict global solar insolation and evaluation of that correlation for Korea(I)”, New & Renew. Energy, 12(S2), p30-35.
[https://doi.org/10.7849/ksnre.2016.10.12.s2.30]

-
Park, S., Kim, J., (2016), “Correlation to predict global solar insolation and evaluation of that correlation for Korea(II)”, New & Renew. Energy, 12(4), p24-29.
[https://doi.org/10.7849/ksnre.2016.12.12.4.024]

-
Lee, K., Zo, I., Jee, J., Choi, Y., (2011), “Temporal and spatial distributions of the surface solar radiation by spatial resolutions on Korea peninsula”, New & Renew. Energy, 7(1), p22-28.
[https://doi.org/10.7849/ksnre.2011.7.1.022]

-
Jee, J., Lee, S., Choi, Y., Lee, K., (2012), “The generation of typical meteorological year for research of the solar energy on the Korean peninsula”, New & Renew. Energy, 8(2), p14-23.
[https://doi.org/10.7849/ksnre.2012.8.2.014]