전산유체/전산구조 연계 방법을 이용한 후퇴각이 있는 수평축 풍력터빈 로터 블레이드의 공탄성 특성 예측
Copyright ⓒ2019 by the New & Renewable Energy
This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The aeroelastic characteristics for the backward swept blade of a horizontal axis wind turbine were examined by using a coupled CFD/CSD method as the fundamental research for a bend-twist coupled (BTC) blade. The aerodynamic loads were obtained from the three-dimensional, incompressible, Navier-Stokes CFD flow solver based on unstructured meshes. The elastic behavior of the blade was calculated by using an FEM-based CSD solver utilizing a nonlinear coupled flap-lag-torsion beam theory. The calculations were made for the blade of the NREL 5MW wind turbine with backward swept angle. Compared to the straight rotor blade, flapwise deflection toward the tower and edgewise deflection toward the leading edge of the backward swept blade were decreased; otherwise, its torsional deflection in nose-down direction was significantly increased. Due to the blade deformations that decreased its effective angle-of-attack, the aerodynamic loads applied to the swept blades were remarkably reduced compared to the straight rotor blade. In addition, the root bending moments were also influenced by the swept-back configuration of the blade. Due to the aerodynamic loads reduction of the backward swept blade, the root bending moments in the edgewise and flapwise directions were decreased, although the torsional bending moments were significantly increased.
Keywords:
Aeroelasticity, Computational fluid dynamics, Computational structural dynamics, Horizontal axis wind turbine, Blade backward swept angle, Bend-twist coupled blade키워드:
공탄성학, 전산유체역학, 전산구조역학, 수평축 풍력터빈, 블레이드 후퇴각, 굽힘-비틀림 연성 블레이드1. 서 론
최근 풍력터빈은 더 많은 전력 생산을 위해 점점 대형화되는 추세이며, 이에 따라 풍력터빈 블레이드에 가해지는 공기역학적인 하중 또한 증가하게 된다. 대형 풍력터빈을 운용함에 있어 블레이드에 가해지는 과도한 하중을 피하기 위해 적절한 하중 제어(Load control)가 요구되며, 이는 능동(Active) 제어 또는 수동(Passive) 제어 방법으로 구현될 수 있다[1].
수동 제어는 블레이드가 돌풍(Gust)으로 인한 이상 하중에 노출되었을 때, 블레이드의 탄성 변형에 따른 받음각 변화를 이용하여 블레이드에 작용하는 하중을 감소시키고, 피로 및 내구 성능을 향상시키는 방법을 말한다. 굽힘-비틀림 연성(Bend-twist coupled, BTC) 블레이드는 대표적인 수동 제어 방법으로, 블레이드의 후퇴 또는 전진각을 이용하여 탄성 변형을 구현하는 형상학적인 방법과 블레이드의 구조 물성치 변화를 이용한 재료적 방법 등이 존재한다[2]. 굽힘-비틀림 연성 블레이드는 블레이드의 피치각 제어를 위한 액추에이터와 같은 기계장치가 요구되지 않기 때문에 능동제어에 비해 풍력발전 시스템의 신뢰성을 확보할 수 있다.
이에 따라 굽힘-비틀림 연성 블레이드의 공탄성 특성을 파악하기 위한 많은 수치적 연구가 수행되었다. Rizitios et al.[3]은 블레이드 요소 운동량 이론과 다물체 동역학 및 오일러 베르누이 빔 이론을 이용하여 후퇴 및 전진각이 있는 풍력터빈 블레이드에 대한 공탄성 해석을 수행하였으며, 블레이드 형상에 따른 공탄성적 거동을 파악하였다. Hansen[4]은 다물체 동역학에 기반한 구조해석자와 블레이드 요소 운동량 이론에 기초한 공력해석자를 이용해 후퇴각이 있는 블레이드에 대한 공탄성 해석을 수행하였으며, 블레이드의 비틀림(Torsion) 변형과 플랩 방향(Flapwise) 변형이 비선형적으로 나타남을 입증하였다. Pavese et al.[5]은 대표적인 풍력터빈 해석 프로그램인 HAWC2 를 이용하여 후퇴각이 있는 10MW 급 풍력터빈 블레이드에 대한 매개변수연구를 수행하였으며, 후퇴각이 블레이드의 공력 하중 및 공탄성 특성에 미치는 영향을 확인하였다.
대부분의 선행 연구에서는 블레이드 요소 운동량 기법에 기반하여 굽힘-비틀림 연성 블레이드에 대한 공탄성 해석이 수행되었다. 그러나 블레이드 요소 운동량 기법의 경우 2차원 에어포일 데이터에 기반하여 공력을 도출하기 때문에 블레이드 끝단 와류 또는 후류에 의한 공기역학적 특성을 예측하는데 한계가 존재하며, 또한 블레이드의 3차원 형상을 고려하지 않기 때문에 후퇴각에 의한 블레이드 단면 변형을 정확히 모사하지 못하는 단점이 존재한다. 이에 따라 본 연구에서는 고도화된 유체해석 기법인 전산유체역학(Computational Fluid Dynamics)에 기반하여 굽힘-비틀림 연성 블레이드에 대한 공탄성 해석을 수행하였다. NREL 5MW[6] 풍력터빈 블레이드에 대해 형상함수를 적용하여 후퇴각이 있는 굽힘-비틀림 연성 블레이드를 모사하였다. 수치해석을 통해 후퇴각이 있는 굽힘-비틀림 연성 블레이드의 탄성 변형을 도출하였으며, 이러한 탄성 변형이 로터 공력 하중 및 블레이드 루트에 작용하는 굽힘 모멘트에 미치는 영향을 확인하였다. 또한 후퇴각의 크기에 따른 탄성 변형 및 공력 하중 변화의 경향성을 확인하였다.
2. 수치해석기법
2.1 유체 해석 기법
본 연구에서 사용된 유동지배방정식은 인공압축성에 기초한 3차원, 점성, 비압축성, Reynolds averaged Navier-Stokes 방정식이며 이를 적분형태로 나타내면 다음과 같다.
| (1) |
| (2) |
식 (1)에서 V와 ∂V는 각각 제어체적 및 제어표면을 나타내며, 은 제어표면에서의 법선 벡터를 나타낸다. t는 비정상 유동해석을 위한 실제 시간(Physical time)을 의미하고, τ는 정상 상태 유동해석을 위한 가상 시간(Pseudo time)을 나타낸다. 와 는 각각 비점성 및 점성 플럭스를 나타낸다.
지배 방정식에 유한체적법(Finite Volume Method)을 적용하기 위해 격자점 중심기법을 사용하였으며, 사면체, 프리즘 격자요소에 대해 메디안-듀얼 방법을 적용하였다. 듀얼 경계면에서의 비점성 플럭스는 공간에 대해 2차 정확도를 갖는 Roe의 Flux Difference Splitting(FDS)[7]를 사용하여 계산하였으며, 점성 플럭스는 중심차분법(Central differencing)[8]을 이용하여 계산하였다. 또한 지배방정식에서의 난류 항을 계산하기 위해 Spalart-Allmaras 난류 모델[9]이 적용되었다. 계산 시간을 절감하고 메모리 한계를 극복하기 위해 모든 해석코드는 병렬화 되었다.
공력에 의해 블레이드의 탄성 변형이 발생할 경우 최종적인 수치해가 도출될 때까지 공력 계산을 위한 새로운 격자계가 요구된다. 새로운 격자계를 구성하는 방법으로 격자 재생성 기법(mesh regeneration)과 격자 변형 기법(mesh deformation)이 널리 알려져 있다.
격자 재생성 기법은 매 단계마다 격자를 재생성하기 때문에 방대한 계산 시간이 요구되므로 본 연구에서는 격자 변형 기법을 이용해 블레이드의 탄성 변형을 모사하였다. 사면체로 구성되는 비점성 격자에서는 스프링 상사 기법에 기반하여 격자변형이 이루어지며, 프리즘 격자로 구성되는 점성 격자에서는 수직 벡터의 기저 분할에 기반한 대수적 방법을 이용하였다[10].
스프링 상사 기법은 초기 격자계의 모든 점이 가상의 스프링으로 연결되어 있고 해당 스프링 시스템이 평형상태에 있다고 가정한다. 새로운 격자계를 생성하기 위해 물체 경계면에서 격자점의 위치변화가 발생하게 되고 이러한 위치변화에 의해 교란된 스프링 시스템은 내부 격자점의 위치를 새롭게 도출하게 된다. 최종적으로 스프링 시스템은 평형 상태에 도달하게 되며 새로운 계산 격자계가 구성된다. 이러한 스프링 시스템을 구현하는데에는 여러 가지 방법이 존재하는데, 본 연구에서는 음의 체적 격자 생성을 방지하고 격자의 질을 비교적 잘 보존하기 위해 Ball-vertex[11] 스프링 기법을 적용하였으며, 최종 선형 시스템은 point Gauss-Seidel을 적용하여 풀이되었다.
2.2 구조 해석 기법
블레이드의 탄성 변형을 모사하기 위해 비선형 항을 고려한 기하학적 정밀 보 모델[12]이 사용되었으며, 축 방향(Axial), 엣지 방향(Edgewise), 플랩 방향(Flapwise), 비틀림 방향(Torsional)의 블레이드 변형이 고려되었다. 블레이드 변형 운동방정식은 해밀턴 변분원리를 이용하여 유도되었으며, 변형이 크지 않다는 가정 하에 오더링 기법(Ordering scheme)[12]을 이용하여 변형 전후의 위치 관계식을 단순화 하였다. 유한요소법(Finite Element Method, FEM)을 이용하여 이산화된 블레이드 변형 운동방정식은 식 (3)과 같다.
| (3) |
식 (3)에서 는 블레이드 탄성 변형을 나타내는 벡터이며, M, G, K는 각각 질량(Mass) 행렬, 자이로스코픽(Gyroscopic) 행렬, 강성(Stiffness) 행렬을 나타낸다. 우변의 는 상수 벡터로 블레이드 회전에 의한 관성력과 관련된 항들을 포함되며, 은 비선형 벡터를 나타낸다. 는 공력해석자에서 계산된 블레이드에 작용하는 공기역학적 하중을 나타내는 벡터이다. 풍력터빈 블레이드에서 발생하는 공력이 정상상태일 경우, 좌변의 시간에 대한 미분항은 생략할 수 있으며 결과적으로 식 (3)은 아래와 같이 정적 평형 방정식으로 나타낼 수 있다.
| (4) |
식 (4)의 운동 방정식은 내재적 시간 적분법인 Newmark-β 기법을 이용하여 풀이되며, 최종적으로 각 방향으로의 비선형성을 고려한 블레이드 구조 변형이 도출된다.
2.3 유체-구조 연계해석 기법
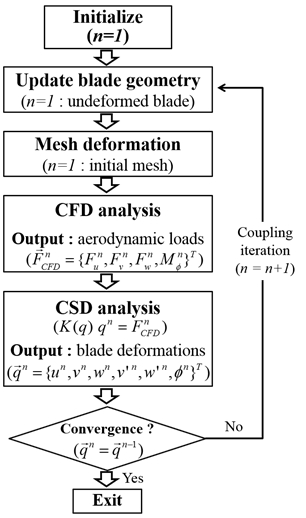
전산유체 및 전산구조 해석자는 상호 연계되어 작동하며 Fig. 1은 본 연구에서 수행된 공탄성 해석의 전체적인 과정을 보여준다. 전산유체 해석자는 블레이드에 가해지는 유체력을 계산하며, 도출된 유체력 정보는 전산구조 해석자에 전달된다. 전산구조 해석자에서는 전달된 유체력 정보를 바탕으로 축 방향, 엣지 방향, 플랩 방향, 비틀림 방향의 블레이드 탄성 구조 변형을 도출하게 된다. 도출된 블레이드 구조 변형 정보는 다시 전산유체 해석자에 전달되며, 격자 변형 기법을 이용해 변형된 블레이드에 대한 새로운 격자계가 생성된다. 전산유체 해석자에 의해 변형된 블레이드에 대한 새로운 유체력이 계산되며, 수렴된 공력 해는 다시 블레이드 탄성 변형 계산을 위해 구조해석자로 전달된다. 이러한 과정은 블레이드의 구조 변형 및 유체력이 최종적으로 수렴될 때까지 반복적으로 수행된다.
3. 결 과
3.1 해석 모델
본 연구에서는 스트레이트 형상의 NREL 5MW 풍력터빈 블레이드[6]에 대해 형상 함수를 적용하여 굽힘-비틀림 연성 블레이드를 모사하였다. 식 (5)는 본 연구에서 사용된 2차 형상 함수로, 선행 연구에서 제시된 모델을 이용하였다[5].
| (5) |
식 (5)에서 a와 b는 형상함수 파라미터로 이에 따라 최종적인 블레이드의 형상이 결정된다. 본 연구에서는 후퇴각에 따른 블레이드의 공력 하중 및 구조변형의 경향성을 파악하기 위해 Table 1과 같이 두 경우의 파라미터를 적용하였다.
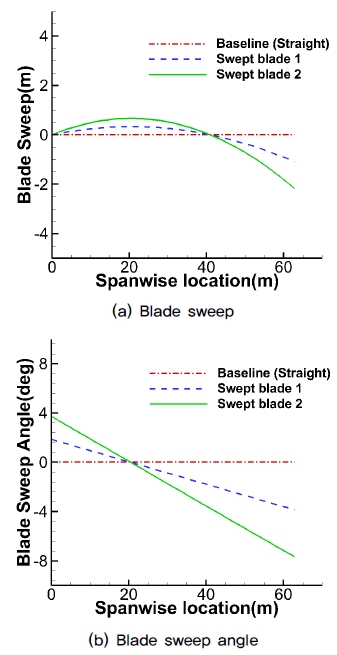
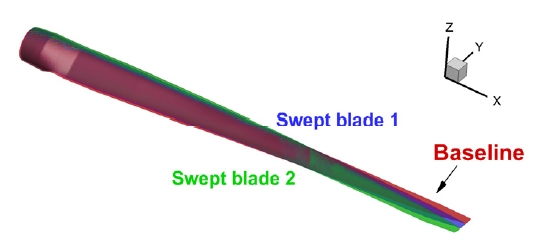
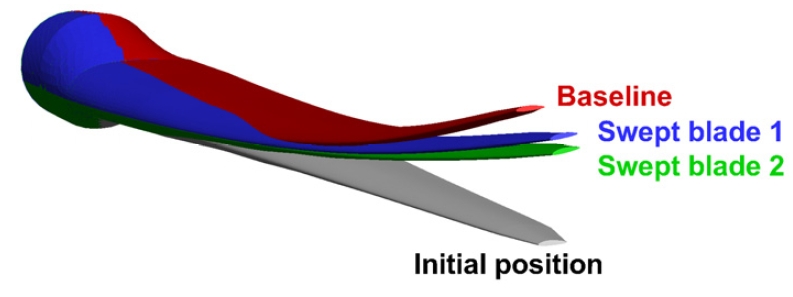
Fig. 2는 각각의 형상 함수 파라미터에 따른 후퇴각이 적용된 블레이드 형상 정보를 나타내며, Fig. 3은 기본형상(Baseline) 블레이드와 후퇴각이 있는 블레이드의 형상 비교을 보여준다. 스트레이트의 기본형상 블레이드에 2차 형상 함수를 적용함에 따라 Fig. 2와 같이 블레이드 스팬 방향으로의 30% 지점까지는 전진각이 적용되며, 그 후로는 후퇴각이 적용된다. Swept blade 1은 로터 끝단에서 약 -4˚의 후퇴각과 블레이드 후방으로 1.1m (0.018R)의 변형이 발생한다. 형상 함수 파라미터가 커질수록 적용되는 블레이드의 후퇴각이 커지며, Swept blade 2는 로터 끝단에서 약 -8˚의 후퇴각과 블레이드 후방으로 2.2m (0.035R)의 변형이 발생한다.
3.2 계산 격자계
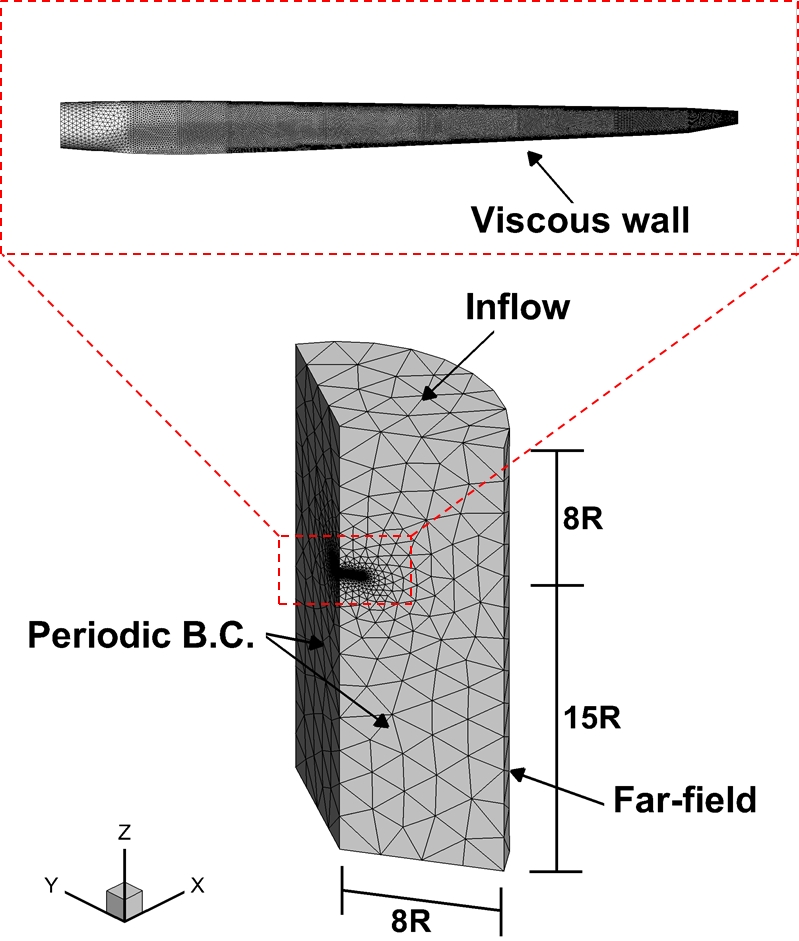
Fig. 4는 해석에 사용된 계산 격자계를 나타낸다. 계산 영역의 원방 경계면은 블레이드 길이의 8배로 설정하였으며, 블레이드로부터 입・출구까지의 거리는 각각 블레이드 길이의 8배, 15배 거리에 위치하도록 하였다. 본 연구에서는 효율적인 계산 수행을 위해 주기적 경계조건을 적용하여 1개의 블레이드에 대한 수치해석을 수행하였다. 자유류의 입구면에서는 inflow, 바깥경계에서는 far-field 조건을 사용하였으며, 블레이드 표면은 점성을 고려할 수 있는 viscous wall로 가정하였다. 블레이드의 형상을 정확히 구현하기 위해 leading edge, trailing edge 및 블레이드 끝단 부근에 조밀한 격자를 분포시켰다. 총 사용된 격자수는 6,032,619개이며 총 2,524,930개의 격자점이 사용되었다.
3.3 해석 결과
후퇴각이 적용된 NREL 5MW 풍력터빈 블레이드에 대해 전산유체-전산구조 해석자를 이용한 공탄성 해석이 수행되었다. 2.5°의 블레이드 코닝각이 적용되었으며, 정상상태 해석을 위해 샤프트 틸트 각은 본 연구에서 고려되지 않았다. 또한 후퇴각으로 인한 블레이드의 형상 변형이 크지 않기 때문에 각 단면에서의 구조물성치는 기본형상 및 후퇴각이 있는 블레이드에 대해 모두 동일하다고 가정하였다. 자유류가 11.5m/s인 정격 풍속 조건에서 수치해석이 수행되었으며, 이때 블레이드의 회전 각속도는 참고문헌 [6]에서 제시된 12.1RPM이 사용되었다. 블레이드의 피치 각은 모든 수치해석에 대해 0°로 설정되었다.
해석자 검증을 위해 정격풍속에서 NREL 5MW 풍력터빈에 대한 수치해석을 수행하였으며, 도출된 결과를 FAST[6]를 이용한 결과와 비교하였다. Table 2는 각 해석자를 이용하여 도출된 로터 추력 및 토크와 블레이드의 구조 변형을 보여준다. 결과를 통해 RANS 기반의 전산유체 해석자와 블레이드 요소 운동량 기법 기반의 FAST 모두 전반적으로 유사한 해를 도출함을 확인할 수 있다. 그러나 FAST의 경우 본 해석 결과에 비해 로터 추력과 블레이드의 플랩 방향(Flapwise) 구조 변형을 더 크게 예측하는데, 이는 블레이드 요소 운동량 기법에 적용되는 이론적 가정의 한계[13,14]로 인해 발생하는 편차로 판단된다.
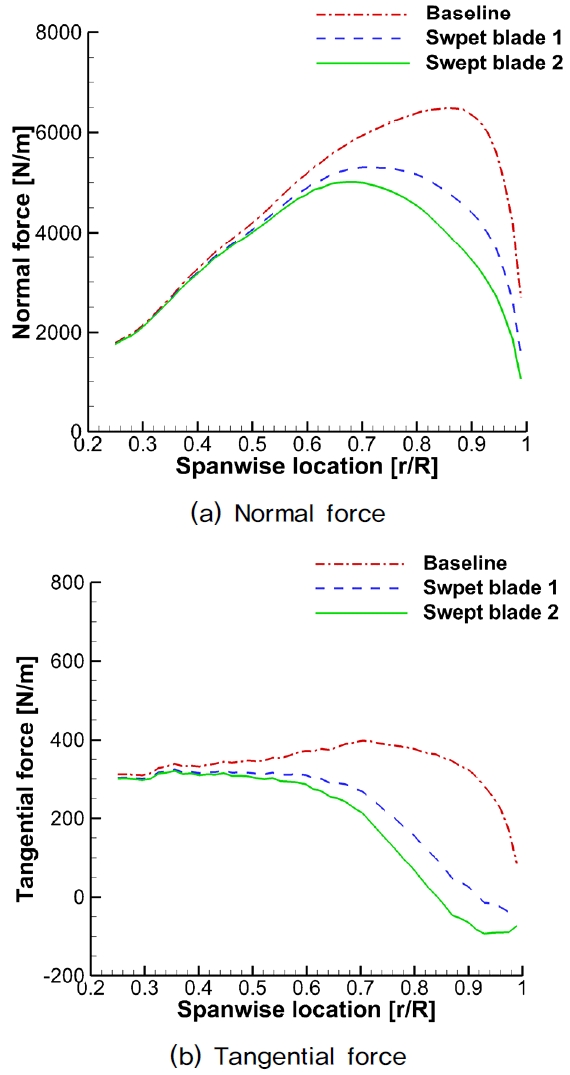
Fig. 5는 블레이드 표면에서의 압력 계수 분포를 나타낸다. 자유류 및 블레이드 회전으로 인해 발생하는 유동장에 의해 블레이드의 압력면(Pressure side)에서는 비교적 높은 압력 분포가 발생하며, 흡입면(Suction side)에서는 낮은 압력 분포가 발생한다. Fig. 5(b), 5(c)에 제시된 후퇴각이 있는 블레이드의 표면 압력 계수 분포는 기본형상 블레이드에 비해 압력면에서는 더 작게 나타나고 흡입면에서는 더 크게 나타난다. 결과적으로 후퇴각이 있는 블레이드는 기본형상 블레이드보다 블레이드에 작용하는 공력 하중이 더 감소하게 된다. Table 3은 유동해석을 통해 예측된 기본형상 블레이드와 후퇴각이 있는 블레이드의 추력 및 토크를 보여준다. 기본형상 블레이드에 비해, 추력의 경우 Swept blade 1은 약 12%, Swept blade 2는 약 25% 감소하였으며, 토크의 경우 Swept blade 1은 약 10%, Swept blade 2는 약 18% 감소하였다. 이러한 공력 하중 감소는 Fig. 6에 제시된 블레이드 스팬 방향으로의 수직력과 접선력 분포에서도 확인할 수 있다. 후퇴각이 존재하는 경우, 기본형상 블레이드에 비해 수직력과 접선력이 큰 폭으로 감소함을 볼 수 있으며, 블레이드의 후퇴각이 커질수록 공력 하중 저하는 크게 나타남을 알 수 있다.
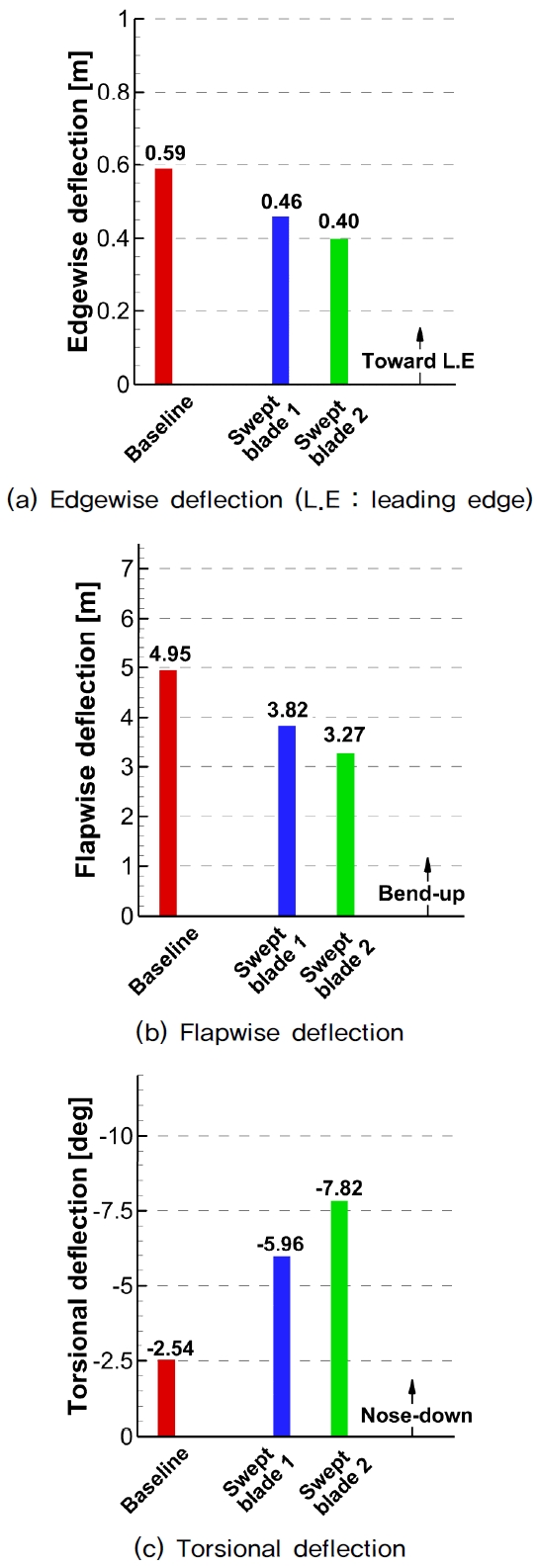
후퇴각이 있는 블레이드에서 발생하는 이러한 공력 하중 감소는 블레이드의 탄성 구조 변형에 의해 지배적으로 영향을 받게 된다. Fig. 7은 공력에 의한 기본형상 및 후퇴각이 있는 블레이드의 탄성 구조 변형을 보여준다. 후퇴각이 있는 블레이드의 경우, 동일한 유동조건에서 기본 형상 블레이드에 비해 플랩방향으로의 구조 변형이 감소하게 되며, 반대로 비틀림 방향으로의 구조 변형은 큰 폭으로 증가한다. 이러한 블레이드의 탄성 변형을 정량적으로 확인하기 위해 각 블레이드의 끝단에서 관찰된 엣지 방향, 플랫 방향, 비틀림 방향으로의 탄성 변형을 Fig. 8에 제시하였다. 후퇴각이 있는 블레이드의 nose-down 방향으로의 비틀림 변형은 기본형상 블레이드에 비해 큰 폭으로 증가하는 것을 확인 할 수 있다. 후퇴각이 존재함에 따라 기본형상 블레이드에 비해 공력 중심이 후방으로 이동하게 되며, 이에 따른 공력 중심과 피치 축(Pitch axis) 간의 오프셋 변화로 인해 후퇴각이 있는 블레이드에서 더 큰 피칭 모멘트가 발생하게 된다. 결국 후퇴각이 있는 블레이드에서 nose-down 방향으로 더 큰 비틀림 변형이 발생되며, 이러한 비틀림 변형의 증가는 블레이드의 각 단면에서의 유효 받음각(Effective angle-of-attack)을 감소시키게 된다. 유효 받음각의 감소는 블레이드에서 발생하는 공력 하중을 감소시키며, 이러한 공력 감소로 인해 후퇴각이 있는 블레이드의 엣지 방향과 플랩 방향으로의 구조 변형은 기본형상 블레이드에 비해 감소한다. Swept blade 1에 비해, Swept blade 2가 후퇴각으로 인한 공력 중심과 피치 축간의 오프셋이 더 크게 변화하기 때문에 Swept blade 2에서 비틀림 변형의 증가 및 공력의 감소가 더 크게 발생하게 된다.
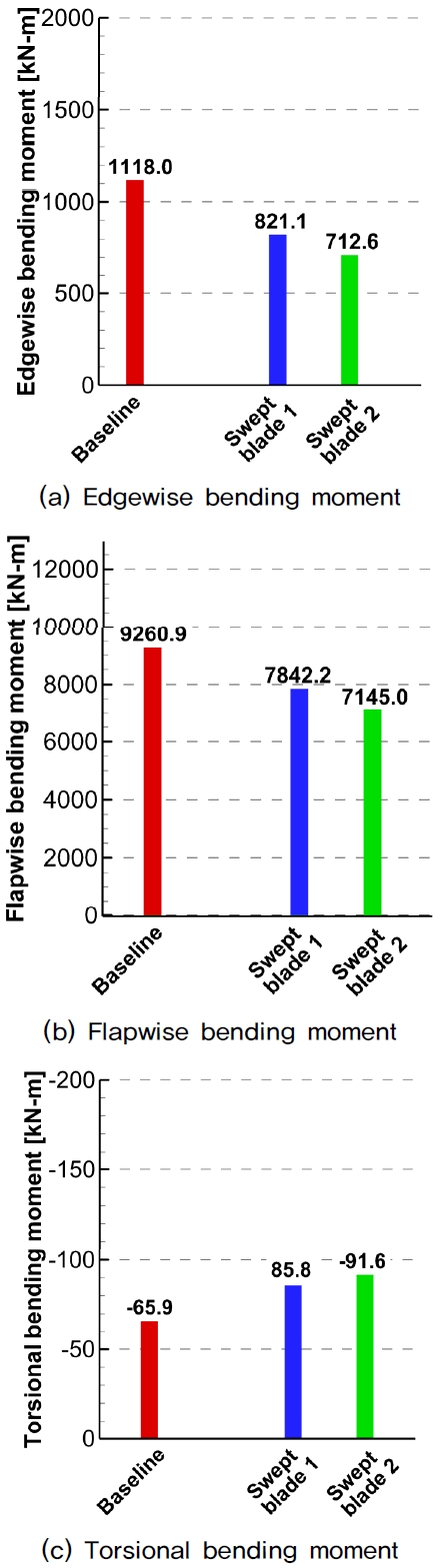
Fig. 9는 엣지 방향, 플랩 방향, 비틀림 방향으로의 블레이드 루트 벤딩 모멘트를 보여준다. 공력 중심과 피치 축 간의 오프셋 변화로 인해 비틀림 방향으로의 벤딩 모멘트가 기본형상 블레이드에 비해 Swept blade 1의 경우 약 30% 증가하며, Swept blade 2는 약 39% 증가한다. 또한 블레이드의 구조 변형으로 인한 받음각 감소에 의해 엣지 방향 및 플랫 방향으로의 블레이드 루트 벤딩 모멘트는 큰 폭으로 감소하는 경향을 보여준다. 기본 형상 블레이드에 비해 Swept blade 1과 Swept blade 2의 루트 벤딩 모멘트는 각각 26%와 36% 감소하였으며, 플랫 방향 벤딩 모멘트는 각각 15%와 33% 감소하였다.
4. 결 론
본 연구에서는 굽힘-비틀림 연성 블레이드의 공탄성 특성을 파악하기 위해 후퇴각이 있는 풍력터빈 블레이드에 대한 수치해석이 수행되었으며, 기본형상 블레이드와의 비교를 통해 후퇴각이 블레이드에서 발생하는 공력 하중 및 탄성 변형에 미치는 영향을 확인하였다. 3차원 점성, 비압축성 RANS 방정식에 기반한 전산유체역학 해석자를 이용해 블레이드 주변에서 발생하는 유동장을 계산하였으며, 비선형 항이 포함된 기하학적 정밀 보 모델에 기반한 전산구조역학 해석자를 이용해 블레이드에서 발생하는 축방향, 엣지 방향, 플랩 방향, 비틀림 방향으로의 구조 변형을 예측하였다. 수치해석을 위해 NREL 5MW 풍력터빈 블레이드에 형상함수를 적용하여 후퇴각이 있는 굽힘-비틀림 연성 블레이드를 구현하였다.
후퇴각으로 인해 블레이드의 nose-down 방향으로의 비틀림 변형이 큰 폭으로 증가하며, 이는 블레이드의 유효 받음각을 감소시킨다. 이러한 받음각의 감소는 결국 블레이드의 공력 하중을 감소시키고, 결과적으로 엣지 방향과 플랫 방향의 블레이드 구조 변형은 감소하게 된다. 또한 후퇴각으로 인해 비틀림 방향의 블레이드 루트 벤딩 모멘트가 증가하며, 엣지 방향, 플랩 방향의 루트 벤딩 모멘트는 감소하게 된다. 이러한 경향성은 블레이드의 후퇴각이 커질수록 더 지배적으로 나타남을 확인하였다.
Nomenclature
| x : | spanwise location on blade, m |
| R : | length of blade span, m |
Acknowledgments
본 연구는 산업통상자원부(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제입니다(No. 20168520021200).
References
-
Johnson, S.J., Baker, J.P., van Dam, C.P., and Berg, D., 2010, “An overview of active load control technique for wind turbines with an emphasis on microtabs”, Wind Energy, 13, 239-253.
[https://doi.org/10.1002/we.356]

-
de Goeij, W.C., van Tooren, M.J.L., and Beukers, A., 1999, “Implementation of bending-torsion coupling in the design of a wind turbine rotor-blade”, Appl. Energy, 63, 191-207.
[https://doi.org/10.1016/S0306-2619(99)00016-1]

- Rizitis, V.A., Voutsinas, S.G., Manolas, D.I., and Politis, E.S., 2010, “Aeroelastic analysis of pre-curved rotor blades”, Proceedings of EWEA 2010, pp. 38-43.
-
Hansen, M.H., 2011, “Aeroelastic properties of backward swept blades”, Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, pp. 1-19.
[https://doi.org/10.2514/6.2011-260]

-
Pavese, C., Kim, T.S, and Murcia, J.P., 2017, “Design of a wind turbine swept blade through extensive load analysis”, Renewable Energy, 102(Part A), 21-34.
[https://doi.org/10.1016/j.renene.2016.10.039]

-
Jonkman, J., Butterfield, S., Musial, W., and Scott, G., 2009, “Definition of a 5-MW reference wind turbine for offshore system development”, National Renewable Energy Laboratory, NREL/TP-500-38060
[https://doi.org/10.2172/947422]

-
Roe, P.L., 1981, “Approximate riemann solver, parameter vectors and difference”, J. Comput. Phys., 43(2), 357-372.
[https://doi.org/10.1016/0021-9991(81)90128-5]

-
Mathur, S.R., and Murthy, J.Y., 1997, “A pressure-based method for unstructured meshes”, Numerical Heat Transfer, Part B: Fundamentals, 31(2), 195-215.
[https://doi.org/10.1080/10407799708915105]

-
Spalart, P.R., and Allmaras, S.R., 1992, “A one-equation turbulent model for aerodynamic flows”, 30th AIAA Aerospace Science Meeting and Exhibit, AIAA Paper 1992-0439
[https://doi.org/10.2514/6.1992-439]

- Lee, H.D., Jung, M.S., and Kwon, O.J., 2009, “Numerical analysis of unsteady viscous flows using a fast grid deformation technique on hybrid unstructured meshes”, Journal of Computational Fluids Engineering, 14(3), 33-48.
-
Bottasso, C.L., Detomi, D., and Serra, R., 2005, “The ball-vertex method : a new simple analogy method for unstructured dynamic meshes”, Comput. Methods Appl. Mech. Eng., 194(39-41), 4244-4264.
[https://doi.org/10.1016/j.cma.2004.08.014]

- Hodges, D.W., Dowell, E.H., 1974, “Nonlinear equations of motion for the elastic bending and torsion of twisted nonuniform rotor blades”, NASA TND-7818, National Aeronautics and Space Administration.
-
Moriarty, P.J., Hansen, A.C., 2005, “AeroDyn theory manual”, National Renewable Energy Laboratory, NREL/TP-500-36881, pp.2-10
[https://doi.org/10.2172/15014831]

-
Lee, H.J., and Lee, D.J., 2019, “Effects of platform motions on aerodynamic performance and unsteady wake evolution of a floating offshore wind turbine”, Renewable Energy, 143, 9-23.
[https://doi.org/10.1016/j.renene.2019.04.134]